Complete Solutions to प्रश्नावली (स्तर 2) (शृंखलाबद्ध-बोधन प्रकार) of chapter रासायनिक बलगतिकी of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | रासायनिक बलगतिकी |
| ARIHANT HINDI | प्रश्नावली (स्तर 2) (शृंखलाबद्ध-बोधन प्रकार) |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
अभिक्रिया का `t_(1//2)` , अभिक्रियकों की सान्द्रता घटकर आधी रह जाने हेतु आवश्यक समय है।
अर्थात् `[A]_t =1/2 [A] implies t_(1//2) = 0.693 // k`
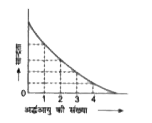
अर्द्धआयु की संख्या इसका अर्थ है कि `t_(1//2)` प्रारम्भिक सान्द्रता से स्वतन्त्र है। चित्र प्रथम कोटि की गतिकी प्रदर्शित करने वाले अभिक्रियकों की सान्द्रता का प्रारूपिक परिवर्तन प्रदर्शित करता है। यह ध्यान देना चाहिए कि यद्यपि प्रथम कोटि की गतिकी का अधिकांश भाग निश्चित समय में पूर्ण हो जाता है परन्तु अभिक्रिया कभी भी समाप्त (रूकेगी) नहीं होगी क्योंकि अभिक्रियकों की सान्द्रता अनन्त समय पर शून्य होगी।
प्रथम कोटि की एक अभिक्रिया का 75%, 32 मिनट में पूर्ण होता है। अभिक्रिया आधी कब पूर्ण होगी?
View Solutionअभिक्रिया का `t_(1//2)` , अभिक्रियकों की सान्द्रता घटकर आधी रह जाने हेतु आवश्यक समय है।
अर्थात् `[A]_t =1/2 [A] implies t_(1//2) = 0.693 // k`
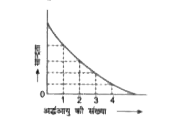
अर्द्धआयु की संख्या इसका अर्थ है कि `t_(1//2)` प्रारम्भिक सान्द्रता से स्वतन्त्र है। चित्र प्रथम कोटि की गतिकी प्रदर्शित करने वाले अभिक्रियकों की सान्द्रता का प्रारूपिक परिवर्तन प्रदर्शित करता है। यह ध्यान देना चाहिए कि यद्यपि प्रथम कोटि की गतिकी का अधिकांश भाग निश्चित समय में पूर्ण हो जाता है परन्तु अभिक्रिया कभी भी समाप्त (रूकेगी) नहीं होगी क्योंकि अभिक्रियकों की सान्द्रता अनन्त समय पर शून्य होगी।
प्रथम कोटि की किसी अभिक्रिया का अर्द्ध-आयुकाल 693 सेकण्ड है। इस अभिक्रिया का वेग नियतांक होगा
View Solutionअभिक्रिया का `t_(1//2)` , अभिक्रियकों की सान्द्रता घटकर आधी रह जाने हेतु आवश्यक समय है।
अर्थात् `[A]_t =1/2 [A] implies t_(1//2) = 0.693 // k`
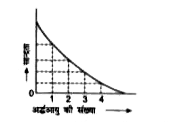
अर्द्धआयु की संख्या इसका अर्थ है कि `t_(1//2)` प्रारम्भिक सान्द्रता से स्वतन्त्र है। चित्र प्रथम कोटि की गतिकी प्रदर्शित करने वाले अभिक्रियकों की सान्द्रता का प्रारूपिक परिवर्तन प्रदर्शित करता है। यह ध्यान देना चाहिए कि यद्यपि प्रथम कोटि की गतिकी का अधिकांश भाग निश्चित समय में पूर्ण हो जाता है परन्तु अभिक्रिया कभी भी समाप्त (रूकेगी) नहीं होगी क्योंकि अभिक्रियकों की सान्द्रता अनन्त समय पर शून्य होगी।
प्रथम कोटि की एक अभिक्रिया का वेग, अभिक्रियक की 0.5 M सान्द्रता `1.5xx10^(-2) "मोल लीटर"^(-1) "मिनट"^(-1)` है। अभिक्रिया की अर्द्धआयु है
View Solutionसमस्त रासायनिक अभिक्रियाएँ उस अवस्था की ओर अग्रसर होती है जिस पर अभिक्रियकों की सान्द्रता अत्यन्त सूक्ष्म हो जायें। यहाँ हम कुछ समीकरणों की गतिकी का अध्ययन करेंगे। माना कोई समीकरण निम्न योजना के अनुसार सामान्यतया प्रदर्शित की जाती है।
`A overset(k_1)underset(k_2)hArrB`
जहाँ, `k_1` तथा `k_2` क्रमशः अग्रगामी तथा पश्चगामी अभिक्रियाओं के वेग नियतांकों को प्रदर्शित करते हैं। इस अभिक्रिया के साम्य स्थिरांक को निम्न प्रकार प्रदर्शित कर सकते हैं। `k = [B]_(oo)//[A]_(oo) = k_(1)// k_2`
स्पीशीज A तथा B की प्रारम्भिक सान्द्रताएँ क्रमशः `[A]_0` तथा `[B]_0` है। t समय पश्चात् माना स्पीशीज A की सान्द्रता `[A]_t` तथा B की सान्द्रता `[B]_t` हो जाती है। `[A]_t` में कुल परिवर्तन का मान निम्न प्रकार दिया गया है
`d[A]_(t//dt)=-k_1[A]_t+k_2[B]_t`
`d[A]_(t//dt)=-k_1[A]_t+k_2([A]_(0)-[A]_t)`
`d[A]_(t//dt)=-(k_1+k_2)([A]_(t)-k_2/(k_1+k_2)[A]_0)`
यदि [C] = 0.4 तथा [A] = 0.6 हो तो अभिक्रिया `2ChArr2A` का `k_c` कितना है?
View Solutionसमस्त रासायनिक अभिक्रियाएँ उस अवस्था की ओर अग्रसर होती है जिस पर अभिक्रियकों की सान्द्रता अत्यन्त सूक्ष्म हो जायें। यहाँ हम कुछ समीकरणों की गतिकी का अध्ययन करेंगे। माना कोई समीकरण निम्न योजना के अनुसार सामान्यतया प्रदर्शित की जाती है।
`A overset(k_1)underset(k_2)hArrB`
जहाँ, `k_1` तथा `k_2` क्रमशः अग्रगामी तथा पश्चगामी अभिक्रियाओं के वेग नियतांकों को प्रदर्शित करते हैं। इस अभिक्रिया के साम्य स्थिरांक को निम्न प्रकार प्रदर्शित कर सकते हैं। `k = [B]_(oo)//[A]_(oo) = k_(1)// k_2`
स्पीशीज A तथा B की प्रारम्भिक सान्द्रताएँ क्रमशः `[A]_0` तथा `[B]_0` है। t समय पश्चात् माना स्पीशीज A की सान्द्रता `[A]_t` तथा B की सान्द्रता `[B]_t` हो जाती है। `[A]_t` में कुल परिवर्तन का मान निम्न प्रकार दिया गया है
`d[A]_(t//dt)=-k_1[A]_t+k_2[B]_t`
`d[A]_(t//dt)=-k_1[A]_t+k_2([A]_(0)-[A]_t)`
`d[A]_(t//dt)=-(k_1+k_2)([A]_(t)-k_2/(k_1+k_2)[A]_0)`
किस समय पर, A की सान्द्रता में परिवर्तन की दर परिणाम में, C की सान्द्रता में परिवर्तन की दर के समान होगी?
View Solutionसमस्त रासायनिक अभिक्रियाएँ उस अवस्था की ओर अग्रसर होती है जिस पर अभिक्रियकों की सान्द्रता अत्यन्त सूक्ष्म हो जायें। यहाँ हम कुछ समीकरणों की गतिकी का अध्ययन करेंगे। माना कोई समीकरण निम्न योजना के अनुसार सामान्यतया प्रदर्शित की जाती है।
`A overset(k_1)underset(k_2)hArrB`
जहाँ, `k_1` तथा `k_2` क्रमशः अग्रगामी तथा पश्चगामी अभिक्रियाओं के वेग नियतांकों को प्रदर्शित करते हैं। इस अभिक्रिया के साम्य स्थिरांक को निम्न प्रकार प्रदर्शित कर सकते हैं। `k = [B]_(oo)//[A]_(oo) = k_(1)// k_2`
स्पीशीज A तथा B की प्रारम्भिक सान्द्रताएँ क्रमशः `[A]_0` तथा `[B]_0` है। t समय पश्चात् माना स्पीशीज A की सान्द्रता `[A]_t` तथा B की सान्द्रता `[B]_t` हो जाती है। `[A]_t` में कुल परिवर्तन का मान निम्न प्रकार दिया गया है
`d[A]_(t//dt)=-k_1[A]_t+k_2[B]_t`
`d[A]_(t//dt)=-k_1[A]_t+k_2([A]_(0)-[A]_t)`
`d[A]_(t//dt)=-(k_1+k_2)([A]_(t)-k_2/(k_1+k_2)[A]_0)`
किसी साम्यावस्था प्रक्रम में `k_f` तथा `k_b` के मध्य निम्न में से कौन-सा सम्बन्ध सही होगा जबकि यह अभिक्रियकों तथा उत्पादों के समान मोल रखता है?
View Solution
प्रश्नावली (स्तर 2) (शृंखलाबद्ध-बोधन प्रकार) questions and complete solutions for chapter रासायनिक बलगतिकी of ARIHANT CHEMISTRY (HINDI) of Class 12
All Exercises from ARIHANT HINDI Class 12 CHEMISTRY रासायनिक बलगतिकी
- उदाहरण
- परीक्षा की तैयारी हेतु प्रश्नावली (लक्ष्य JEE MAIN )
- परीक्षा की तैयारी हेतु प्रश्नावली (लक्ष्य JEE MAIN ) (विगत वर्षों के प्रश्न )
- प्रश्नावली (स्तर 1)
- प्रश्नावली (स्तर 2)
- प्रश्नावली (स्तर 2) (एक या एक से अधिक विकल्प सही हैं )
- प्रश्नावली (स्तर 2) (कथन-कारण प्रकार)
- प्रश्नावली (स्तर 2) (शृंखलाबद्ध-बोधन प्रकार)
- प्रारम्भिक प्रश्नावली 1
- प्रारम्भिक प्रश्नावली 2
- विगत वर्षों के प्रश्न
- साधित उदाहरण