Complete Solutions to प्रश्नावली (स्तर 1) of chapter त्रिभुजों के गुण,ऊंचाई एवं दुरी of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | त्रिभुजों के गुण,ऊंचाई एवं दुरी |
| ARIHANT HINDI | प्रश्नावली (स्तर 1) |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
`Delta ABC ` में , ` cosec A ( sin B cos C + cos B sin C) ` का मान है
View Solutionयदि ` Delta ABC ` में , ` 2b^(2) =a^(2) +c^(2) ` , तब ` (sin 3B)/( sin B) ` का मान है
View Solution`sin A : sinC =sin (A-B) : sin (B-C) , ` तब ` a^(2) , b^(2) ,c^(2) ` है
View Solutionयदि किसी त्रिभुज की भुजाएं `a,b,c` है,तब
View Solution` Delta ABC ` में , यदि ` 2s =a+ b +c `
` (s-b) (s-c) -x sin ^(2)""(A)/( 2) ,` तब `x` का मान है
View Solutionएक त्रिभुज के कोनों में`4 : 1 : 1` का अनुपात है। उस त्रिभुज की सबसे बड़ी भुजा और परिमाप का अनुपात होगा
View Solutionत्रिभुज `ABC ` में यदि `/_ C= 60^(@)` हो तो सिध्द कीजिए -
`(1)/(a+c) +(1)/(b+c) =(3)/(a+b+c)`
View Solutionयदि `DeltaABC` में `a,b,c` समांतर श्रेणी में हों तो `("sin"A/2"sin"C/2)/("sin"B/2)` का मान है
View Solutionएक त्रिभुज में , दो बड़ी भुजाओं की लम्बाई क्रमशः 10 सेमि तथा 9 सेमि है। यदि त्रिभुज के कोण समांतर श्रेणी में है , तब tisri भुजा की लम्बाई हो skti है
View Solution` Delta ABC` की भुजा `BC` पर बिंदु `D` व `E` इस प्रकार है की ` BD = DE = EC , ` यदि ` angle BAD =x, angle DAE =y, angle EAC =z , ` तब ` (sin ( x+ y)sin ( y+z) )/( sin x sinz) ` का मान है।
View Solution` Delta ABC ` में , यदि ` a= 2x , b= 2y ` तथा `angle C = 120^(@) ,` तब त्रिभुज का क्षेत्रफल है।
View Solution` Delta ABC ` में यदि ` tan"" (A)/(2) tan ""(C)/(2) = (1)/(2) , ` तब `a,b,c` है।
View Solution`DeltaABC` में यदि `2s=a+b+c`, तो `(s(s-a))/(bc)-((s-b)(s-c))/(bc)` का मान है
View Solution` Delta ABC ` में, ` (b+c-a) tan ""(A)/(2) ` बराबर है।
View Solution`Delta PQR ` में, ( चित्रानुसार ) दिया है की `x: y : z =2: 3: 6, ` तब ` angle QPR ` बराबर है
` (##ARH_HIN_ASP_JEE_MN_MAT_P1_C10_E02_015_Q01.png" width="80%">
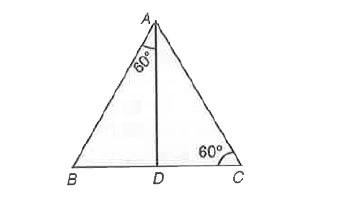
View Solution` Delta ABC ` में `AD` माध्यिका है तथा ` angle A = 60^(@) `तब, ` 4AD^(2) ` बराबर है
View Solutionयदि ` cos ^(2) A + cos ^(2) C = sin ^(2) B, ` तब ` Delta ABC ` है।
View Solution`Delta ABC ` में , `a=5,b=7` तथा `sin A = (3)/(4) ` तब संभव त्रिभुजों की संख्या है।
View Solutionयदि `Delta ABC ` के शीर्षों `A,B,` व् C से खींचे गए शीर्षलम्ब की लम्बाई क्रमशः ` p_1,p_2` व् ` p_3` है , तब ` p_1^(-2) +p_2^(-2) +p_3^(-2) ` का मान है
View Solutionयदि त्रिभुज की भुजाओं `a,b,c` पर डाले गए लंबों की लम्बाई `x,y,z` है, तब `(bx)/( c) + ( cy)/( a) + ( az) /( b) ` का मान है।
View Solutionयदि `Delta ABC ` में, `angle ACB ` का समद्विभाजक CD है ,तब CD बराबर है
View Solution`Delta ABC ` में, ` (a-b) ^(2) cos ^(2) ""(C)/(2) +( a+b) ^(2) sin ^(2) ""(C)/(2) ` के बराबर है।
View Solution`Delta ABC ` में , `a: b: c = 4: 5: 6 ,` तब परिवृत व अन्तः वृत की त्रिज्याओं का अनुपात है
View Solutionचक्रीय चतुर्भुज की संग्लन भुजाएं `2` व `5` है तथा इनके बीच का कोण ` 60^(@) ` है। यदि तीसरी भुजा `3` है , तब चौथी भुजा है
View Solutionएक त्रिभुज जिसकी भुजाएं `3,5,6` है, के अन्तः वृत की त्रिज्या है
View Solution`Delta ABC ` में, `cos A + cos B +cos C ` बराबर है
View Solutionयदि `(1-( r_1)/(r_2))(1-( r_1)/( r_3) ) = 2,` तब त्रिभुज है
View Solutionयदि त्रिभुज की भुजाओं में , `3: 7: 8` का अनुपात है, तब `R: r` का मान है।
View Solutionयदि `r_1gt r_2gtr_3` ,तब
View Solutionनिम्न कथनों पर विचार कीजिए
`I.` यदि `Delta ABC ` में, `(sin A)/( sinC) =( sin (A-B))/( sin (B-C)) ` तब, `a^(2), b^(2) , c^(2) ` समांतर श्रेणी है
`II` यदि `Delta ABC ` में बहिवृत की त्रिजायें `r_1,r_2,r_3` हरात्मक श्रेणी में है , तब भुजाएं `a,b,c` समांतर श्रेणी में है।
इनमें से सही कथन है
View Solution`Delta ABC ` में, `a cot A + b cot B + c cot C ` का मान होगा।
View Solution`1/r_(1)^(2) + 1/r_(2)^(2) + 1/r_(3)^(2) + 1/r^(2) ` का मान है
View Solutionसमबाहु त्रिभुज में , अन्तः वृत , परिवृत तथा बहिवृत की त्रिजायाओं का अनुपात है
View Solutionयदि `r_1,r_2,r_3` किसी त्रिभुज का बाह्य त्रिज्याएँ हो, तब `r_1r_2+ r_2r_3+r_3r_1` का मान होगा
View Solutionयदि 6 मी लम्बाई का एक ठंडा किसी टॉवर के शिखर पर इस प्रकार स्थित है की धरातल पर उसकी छाया की लम्बाई `2sqrt3 ` मी हो , तो सूर्य द्वारा धरातल पर बनाया गया कोण (अंश में ) होगा
View Solutionयदि सूर्य का उन्नयन कोण `45^(@) ` से `30^(@) ` में परिवर्तित होता है , तो टॉवर की छाया 60 मी बढ़ जाती है। टॉवर की ऊंचाई है
View Solution10 मी ऊँची दीवार के शिखर पर 20 मी ऊँचे झंडे का धरातल पर स्थित बिंदु से उन्नयन कोण का स्पर्शज्या `0.5` है। यदि दीवार द्वारा धरातल पर स्थित बिंदु का उन्नयन कोण `theta ` है तो ,
View Solutionएक सीढी क्षेतिज से `alpha` कोण बनाती है। हुई दीवार के सहारे खडी है। सीढी का निचला सिरा दीवारा से दूर X सेमी खीचा जाता है। तब सीढी का ऊपरी सिरा दीवार के साथ y सेमी नीचे खिसक जाता हैं तथा सीढी क्षैतिज के साथ कोण `beta` बनाती है। सत्य सम्बन्ध है।
View Solutionh मीटर ऊंचाई वाले टॉवर के शिखर तथा शिखर पर लगे खम्भे का टॉवर के पाद से 2h मी दुरी पर स्थित्त बिंदु से उन्नयन कोण समान है , तो खम्भे की ऊंचाई होगी। h
View Solution`100` मी ऊंचाई वाले भवन के शिखर का , सामने स्थित भवन की खिड़की पर उन्नयन कोण समकोण है। यदि खिड़की की ऊंचाई `64` मी हो , तो दोनों भवनों की बीच की दुरी होगी।
View Solution300 मी ऊँचे टॉवर के शिखर पर खड़ा प्रेक्षक , एक ही दिशा में तैरने वाले दो नावों का अवनमन कोण क्रमशः `60^(@) ` तथा ` 30^(@) ` मापता है। दोनों नावों के बीच की दुरी होगी।
View Solutionदो टावरों के बीच की दुरी `60` मी है तथा प्रथम टॉवर के शिखर का , द्वितीय टॉवर के शिखर पर अवनमन कोण `30^(@) ` है। यदि द्वितीय टॉवर की ऊंचाई `150` मी हो, तो प्रथम टॉवर की ऊंचाई होगी
View Solutionधरातल से 1 कमी की ऊंचाई पर उड़ रहे हवाई जहाज का , धरातल पर स्थित किसी बिंदु पर उन्नयन कोण `60^(@) ` है तथा 10 सेकंड पश्चात उन्नयन कोण ` 30^(@) ` मापा जाता है। हवाई जहाज की एकसमान गति (किमी/ घंटे में) होगी।
View Solutionकिसी भवन के शिखर तथा शिखर झंडे का भवन के पाद से 40 मी दूर स्थित बिंदु पर उन्नयन कोण क्रमशः `60^(@) ` तथा `30^(@) ` है, तब झंडे की ऊंचाई होगी
View Solutionधरातल पर स्थित बिंदु पर, किसी टॉवर के उन्नयन कोण का कोज्या ` (3)/(5) ` है। टॉवर की और 32 मी चलने पर टॉवर के उन्नयन कोण का कोज्या `(2)/(5)` हो जाता है। टॉवर की ऊंचाई है
View Solutionh मीटर ऊँचे खम्भे के पद पर, किसी टॉवर के शिखर का उन्नयन कोण `alpha ` है तथा खम्भा टॉवर के शीर्ष पर ` beta ` बनाता है , तब टॉवर की ऊंचाई है
View Solutionकिसी पाहड़ी के शिखर का, किसी h मीटर ऊँचे भवन के शिखर तथा पाद पर उन्नयन कोण क्रमशः p तथा q है। पहाड़ी की ऊंचाई है
View Solutiona मीटर पहाड़ी के शिखर का, किसी निश्चित h मीटर ऊँचे टॉवर के पाद पर बना अवनमन कोण , टॉवर के शिखर पर बने उन्नयन कोण का दोगुना है। यदि `theta ` उन्नयन कोण हो , तो `theta ` का मान है
View Solutionकिसी झील के ऊपर ,a मीटर की ऊंचाई पर बादलों के किसी बिंदु का उन्नयन कोण `alpha ` तथा प्रवर्तन का अवनमन कोण `beta ` है , तब बादलों की ऊंचाई है
View Solutionकिसी 25 मी ऊँचे भवन के शिखर पर 5 मी uncha झंडा लगा है। 30 मी की ऊंचाई पर एक प्रेक्षक , झंडे के शिखर तथा भवन के शिखर पर समान कोण मापता है। प्रेक्षक की , झंडे के शिखर से दुरी है।
View Solutionकिसी चिमनी के शिखर तथा पाद पर, किसी दूसरी चिमनी , जिसकी ऊंचाई 150 मी तथा पहली चिमनी के समान धरातल पर है , का अवनमन कोण क्रमशः `theta ` तथा `phi ` है, तब उनके शिखरों के बीच की दुरी होगी जबकि ` tan theta = (4)/(3) ` तथा ` tan phi = (5)/(2)`
View Solutionकिसी 60 मी ऊँचे टॉवर के शिखर का , किसी भवन के शिखर तथा पाद पर अवनमन कोण क्रमशः `alpha ` तथा `beta ` है। यदि भवन की ऊंचाई `(60 sin ( beta -alpha ))/( x) ` हो, तो x का मान है
View Solutionधरातल पर त्रिभुज बनाने वाले तीन बिंदुओं `A,B,C ` में से प्रत्येक का किसी टॉवर के शिखर पर उन्नयन कोण `alpha ` है। यदि ` R, Delta ABC ` की परित्रिज्या हो, तो टॉवर की ऊंचाई है
View Solutionएक r त्रिज्या का गोलीय गुब्बारा , किसी प्रेक्षक की आँख पर `alpha ` कोण बनाता है। यदि गुब्बारे के केंद्र का उन्नयन कोण `beta ` हो, तो गुब्बारे के केंद्र की ऊंचाई है
View Solutionकिसी दीवार के सहारे खड़ी एक सीढी धरातल पर `alpha ` कोण आन्तरित करती है। सीढी का पाद, दीवार से `a_1` दुरी तक इस प्रकार खिंचा जाता है की सीढी दीवार पर `b_1` दुरी निचे खिसक जाती है। तथा धरातल पर `beta ` कोण आन्तरित करती है। पुनः सीढी का पाद , दीवार से `a_2` दुरी तक इस प्रकार खिंचा जाता है की सीढी दीवार पर `b_2` दुरी निचे खिसक जाती है तथा धरातल पर `gamma ` कोण आन्तरित करती है।यदि `a_1a_2 =b_1b_2` हो, तो
View SolutionABC एक त्रिभुजाकार पार्क है जिसमे AB= AC = 100 मी है। BC के मध्य -बिंदु पर एक सीधी मीनार खड़ी है । यदि मीनार के शिखर के बिन्दुओ A तथा B पर उन्नयन कोण क्रमश `cot^(-1) (3 sqrt2)` तथा `cosec^(-1) (2sqrt2)` है, तो मीनार की ऊंचाई (मीटर में) है
View Solutionकिसी टॉवर के शिखर का टॉवर के दक्षिण में स्थित बिंदु A पर उन्नयन कोण `alpha `तथा टॉवर के पूर्व में स्थित बिंदु B पर उन्नयन कोण `beta ` है। यदि AB = d हो, तो टॉवर की ऊंचाई है
View SolutionABCD एक वर्गाकार प्लाट है । बिंदु D पर स्थित टॉवर के शिखर का बिंदु A या C पर उन्नयन कोण `30^(@) ` तथा बिंदु B पर ` theta ` है ,तब `tan theta ` का मान है
View Solutionएक ऊर्ध्वाधर टॉवर , समतल से ` 15^(@) ` पर झुके ढलान पर स्थित है , खम्भे के पास से ढलान पर एक आदमी 80 फुट चढ़ता है। जहाँ पर टॉवर के शिखर का उन्नयन कोण ` 30^(@) ` है टॉवर की ऊंचाई है
View Solutionयदि किसी सिधि नदी के एक किनारे पर दो बिंदु A तथा B है तथा दूसरे किनारे पर दो बिंदु C तथा D है। यदि A से B की दिशा तथा C से D की दिशा समान हो तथा `AB = a,angle CAD = alpha , angle DAB = beta,angle CBA= gamma` हो,तो CD का मान है
View Solutionकिसी बिन्दु से पहाडी के शिखर का उन्नयन कोण `alpha` है क्षैतिज से `beta` कोण वाली ढलान पर उस बिन्दु से b दूरी ऊपरी की ओर चलने पर पहाडी के शिखर का उन्नयन कोण बढकर `gamma` हो जाता है तो पहाडी की ऊँचाई होगी।
View Solutionएक झील की सतह से 2500 मीटर ऊपर एक बिन्दु से एक बादल का उन्नयन कोण `15^(@) ` तथा परावर्तन का अवनमन कोण `45^(@) ` है। झील के पृष्ट से बदल की ऊंचाई है
View Solution
प्रश्नावली (स्तर 1) questions and complete solutions for chapter त्रिभुजों के गुण,ऊंचाई एवं दुरी of ARIHANT MATHS (HINDI) of Class 12