Complete Solutions to प्रश्नावली (लक्ष्य JEE MAIN) of chapter सीमा , सतत्ता एवं अवकलनीयता of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सीमा , सतत्ता एवं अवकलनीयता |
| ARIHANT HINDI | प्रश्नावली (लक्ष्य JEE MAIN) |
| Number Of Questions | 44 |
| Academic Year | 2023-24 |
`lim_(x→2)(2^x-x^2)/(x^x-2^2)` का मान है
04:23View Solutionयदि f एक पूर्णतः वर्धमान फलन है तब `lim_(xrarr0) (f(x^2)-f(x))/(f(x)-f(0))` का मान होगा
01:43View Solutionयदि `e^(2x)y=2y+sin^2x` हो तो `x=0` पर `dy/dx` का मान ज्ञात कीजिये ।
05:08View Solutionयदि `f(x) = (1+ b^2)x^(2) +2bx + 1` है तथा b के एक दिए गए मान के लिए f(x) का न्यूनतम मान m(b) है। b के परिवर्तित होने पर m(b) की परास है
04:42View Solution`lim_(n to oo)sin[pisqrt(n^(2)+1)]` का मान है
03:23View Solutionयदि `f(x)={(e^(x),x le 0),(|1-x|,x gt0):}` तब
07:22View Solutionफलन `f(x)=|x|+(|x|)/(x)` है
05:39View Solution`lim_(n rarr oo) (1)/(1.3)+(1)/(3.5)+(1)/(5.7)+(1)/(7.9)+.....` का मान होगा
05:04View Solution`lim_(x rarr oo) ((3x-4)/(3x+2))^((x+1)/3)` का मान है
03:51View Solutionयदि `f'(2)= 6` और `f'(1)= 4`, तब `lim_(h rarr0)(f(2h +2+ h^2)-f(2))/(f(h-h^2+1)-f(1))` का मान है
02:47View Solutionयदि `f(x) = cot^(-1)((3x-x^3)/(1-3x^2))` और `g(x) = cos^(-1)((1-x^2)/(1+x^2))` तब , `lim_(x rarra)(f(x)-f(a))/(g(x)-g(a)), 0 lt a lt 1/2 ` का मान है
04:16View Solutionयदि `f(x)=|(sinx, cos x , tan x),(x^3,x^2,x),(2x,1,1)|` , तब `lim_(x rarr0)(f(x))/(x^2)` का मान है
03:52View Solution`lim_( x rarr pi//2)[x tan x - (pi/2) secx]` का मान होगा
02:29View Solution`lim_(xrarrpi/2)(int_(x//2)^(x)tdt)/(sin(2x-pi))` का मान होगा
02:47View Solutionयदि `lim_(x rarr 0) (log(a + x)-loga)/(x)+klim_(x rarre)(logx-1)/(x-e)` =1 तब
05:09View Solutionमाना `f:R rarr P` एक अवकलनीय फलन है तथा `f(2) = 6 , f'(2) =1/48` है, तब `lim_(x rarr 2) int_(6)^(f(x)){4t^3dt)/(x-2)` का मान है
05:25View Solution`lim_(n rarroo)[1/(n^3+1)+4/(n^3+1)+9/(n^3+1)+.....+n^2/(n^3+1)]` का मान होगा
02:39View Solution`lim_(n - oo)cos(x/2)cos(x/4)cos(x/8).....cos(x/2^n)` का मान है
05:19View Solutionयदि `f(x) = {{:(x^2sin""1/x,x ne 0),(0,0):}` तब
04:52View Solutionफलन `f(x)={{:(-1,xlt0),(0,x=0),(1,xgt0):}` तथा `g(x)=sinx+cosx` हो, तो `f{g(x)}` के अन्तराल `(0,2pi)` में असतत बिन्दु है
05:01View Solution`f(x) = {{:(tan^(-1)x,|x|lt1),(1/2(|x|-1),|x|gt1):}` के अवकलज का प्रान्त क्या होगा?
05:27View Solutionयदि ` f(9) = 9,f'(9) = 4,` तब `lim_(x rarr 9)(sqrt(f(x))-3)/(sqrtx-3)` का मान है
02:45View Solution`lim_(x rarr0)((a^(x)+b^x+c^x)/3)^(2//x), (a, b, c gt0)` का मान होगा
04:09View Solution`lim_(x rarroo)(x^2sin(1/x)-x)/(1-|x|)` का मान होगा
02:20View Solutionयदि `lim_(x rarroo)((x^2+1)/(x+1)-alphax-beta)=0` हो, तो `alpha` व `beta` के मान होंगे
03:12View Solution`lim_(n rarroo)(1+2+3+.....+n)/(n^2+100)` का मान होगा
02:06View Solutionमाना `f(x)={{:(x+a,xlt0),(|x-1|,xge0):}` तथा `g(x)={{:(x+1,xlt0),((x-1)^(2)|+b,xge0):}` जहाँ, a तथा b ऋणोंत्तर वास्तविक संख्याएँ है।
यदि `(gof)x` सभी वास्तविक `x` पर सतत हो, तो a का मान है08:41View Solutionमाना `f(x)={{:(x+a,xlt0),(|x-1|,xge0):}` तथा `g(x)={{:(x+1,xlt0),((x-1)^(2)|+b,xge0):}` जहाँ, a तथा b ऋणोंत्तर वास्तविक संख्याएँ है।
यदि `(gof)x` सभी वास्तविक `x` पर सतत हो, तो a का मान है08:41View Solution`lim_(xto0)(sin pi(cos2x+sin^2x))/x^2`का मान है
03:59View Solutionयदि `G(x)=-sqrt(25-x^2)` तब सिद्ध कीजिये `lim_(xto1)(G(x)-G(1))/(x-1)``=1/sqrt(24)`
05:18View Solutionवक्तव्य I यदि `a_(1),a_(2),....,a_(n)gt0` हो, तो `lim_(x to oo)((a_(1)^(1/x)+a_(2)^(1/x)+...+a_(n)^(1/x))/(n))^(nx)=a_(1)a_(2)...a_(n)`
वक्तव्य II यदि `lim_(x to a)f(x)=1,lim_(x to a)g(x)=oo` हो, तो `lim_(x to a){f(x)}^(g(x))=e^(x to a^(limg(x){f(x)-1}))`08:29View Solutionवक्तव्य I `lim_(x to 0)(sqrt(1-cos2x))/(x)` विद्यमान नहीं है।
वक्तव्य II `|sinx|={{:(sinx,0ltxltpi//2),(-sinx,-pi//2ltxlt0):}`05:48View Solutionवक्तव्य I फलन `f(x)=(1)/({x})` पूर्णाकीय मानों पर असतत है। जहाँ, `{*}` भिन्नात्मक भाग फलन है।
वक्तव्य II x के पूर्णाकीय मानों के लिए `f(x)` परिभाषित नहीं है।03:59View Solutionमान लीजिए `f(x) = ((27-2x)^(1//3)-3)/(9-3(243+5x)^(1//5))`
वक्तव्य । यदि फलन f(x) प्रत्येक बिन्दु पर सतत् हो, तब f(0) = 2 होगा।
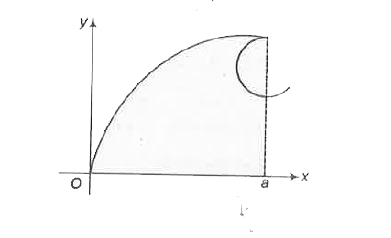
वक्तव्य ॥ फलन के सतत् होने के लिए `lim_(x rarr0) f(x) = f(0)` होगा।06:54View Solutionवक्तव्य । फलन f(x) जो निम्न ग्राफ द्वारा प्रदर्शित है, x = a पर अवकलनीय है।
वक्तव्य ॥ फलन f(x), x = a पर सतत् है।
 03:24View Solution
03:24View Solution`lim_(xto pi//4)(underset(2)overset(sec^(x)x)intf(t)dt)/(x ^(2)-(pi^(2))/(16))=`
04:23View Solutionयदि `lim_(x rarr0)([(a-n)nx-tanx]sinnx)/(x^2)=0` जहाँ n एक अशून्य वास्तविक संख्या है, तो a बराबर है
03:37View Solutionमाना `f:Rrarr R` इस प्रकार है कि f(1) = 3 और "(1) = 6 तब `lim_(x rarr0)[(f(1+x))/(f(1))]^(1//x)` बराबर है
04:36View Solution`f(x)=[x]sin(pix)` का x = k पर, जहाँ k एक पूर्णांक है, बायाँ अवकलज है
09:44View Solutionमाना `f(x) =x^3-x^2+x+1` और `g(x) ={{:(max{f(t),0let,lex},0lexle1),(3-x,1ltxle2):}` फलन g(x) बिन्दु (0, 2) पर होगा
08:34View Solutionयदि `f :[-1,1]rarr R `और `f '(0) = lim_(n rarroo) nf(1//n)` और f(0) = 0, तब `lim_(n rarroo)(2)/pi(n+1)cos^(-1)(1/n)-n` का मान क्या होगा? जब `0lt|lim_(nrarroo)cos^(-1)(1/n)|ltpi/2`
05:24View Solutionमाना f(x), अन्तराल [-2,2] पर इस प्रकार परिभाषित है कि, `f(x) ={{:(-1,-2lexle0),(x-1,0ltxle2):}` में फलन f(x) होगा
05:27View Solutionयदि `f(x) = cot^(-1)((3x-x^3)/(1-3x^2))` तथा `g(x) =cot^(-1)((1-x^2)/(1-x^2))` तब `lim_( x rarr a) (f(x)-f(a))/(g(x)-g(a))` है, जबकि ` a lt a lt 1/2`
04:16View Solution`f(x) = [x]cos ((2x-1)/2)pi, [x]` महत्तम पूर्णांक फलन को प्रदर्शित करता है, असतत् है।
08:50View Solution
प्रश्नावली (लक्ष्य JEE MAIN) questions and complete solutions for chapter सीमा , सतत्ता एवं अवकलनीयता of ARIHANT MATHS (HINDI) of Class 12
