Complete Solutions to बहुविकल्पीय प्रश्न of chapter यूनिट टेस्ट 3 (त्रिकोणमिति ) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | यूनिट टेस्ट 3 (त्रिकोणमिति ) |
| ARIHANT HINDI | बहुविकल्पीय प्रश्न |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
यदि `sin theta =n sin ( theta +2alpha)` , तब `tan ( theta+ alpha)` का मान है
View Solutionयदि A तृतीय चतुर्थांश में है तथा `3tanA-4= 0` , तब `5sin2A-3sin A+ 4cos A` का मान है
View Solution`sin^(6)x +cos^(6)x` का मान निम्न के बीच है
View Solutionव्यंजक `sin alpha + sinbeta + singamma` का निम्निष्ठ मान, जबकि `alpha , beta, gamma` वास्तविक संख्याएँ हैं, जो `alpha + beta + gamma = pi` को सन्तुष्ट करती हैं, है।
View Solution`27^(cos2x)81^(sin2x)` का न्यूनतम मान है
View Solutionयदि `n= (pi)/(4alpha)` तब `tan alpha tan2alpha tan 3alpha ....tan (2n-1)alpha` का मान है
View Solution`2-cos x + sin^2 x` के महत्तम एवं लघुत्तम मान का अनुपात है
View Solution`12 sin theta - 9 sin^2 theta` का महत्तम मान है
View Solutionयदि `m =acos^(3) theta + 3acos thea sin^2e theta` ,
`n = asin^(3)thea + 3aços^(2)sintheta` , तब `(m + n)^(2//3) + (m-n)^(2//3)` का मान है
View Solutionयदि `a sin^(2) alpha -1/(a)"cosec"^(2) alpha = 0, 0 lt alpha ltpi/2,` तब `cos^(2) alpha + 5sinalphacos alpha + 6sin^2 alpha` का मान है
View Solutionयदि `0^@ lt theta lt 180^@` , तब `sqrt(2+sqrt(2+sqrt(2+....+sqrt(2(1+costheta)))))` का मान है (जहाँ 2 की सख्या n है)
View Solutionमाना n एक विषम पूर्णांक है , यदि `sin n theta = sum _(r=0)^(n) b_(r) sin^(r) theta , AA theta in R` तब
View Solutionयदि `sin^(2)x + asin x + 1 = 0` कोई भी वास्तविक हल नहीं रखता है, तब
View Solutionयदि `tan""(x)/2 = "cosec" x - sin x`, तब `tan^(2)""(x)/2` का मान है
View Solutionयदि `sum_(i=1)^(2n)cos^(-1)x_(i)=0` , तब `sum_(i=1)^(2n)x_i` का मान है
View Solution`1+ sin^(4) 2x = cos^(2)6x` का व्यापक हल है
View Solutionसमीकरण `2cos^(2)""x/2sin^(2) x = x^2 + x^(-2) ,0 lt xle pi/2` का/के
View Solutionएक 10 मी ऊँचे खम्भे के पाद एवं शीर्ष से टावर के शीर्ष के उन्नयन कोण क्रमशः `30^@` व `60^@` हैं। टावर की ऊँचाई है
View Solutionx के किस मान के लिए, `cos^(-1) (cos 4)gt 3x^(2) - 4x` है?
View Solutionकिसी पहाड़ी के पश्चिम में स्थित बिन्दु P से पहाड़ी का उन्नयन कोण `60^@` है तथा दक्षिण में स्थित बिन्दु से उन्नयन कोण `30^@` है। यदि PQ = 200 मी, तब पहाड़ी की ऊँचाई है ।
View Solutionदो चिमनियाँ समान समतल पर खड़ी हैं। एक चिमनी जो 150 मी ऊँची है, की चोटी तथा पाद से दूसरी चिमनी की चोटी के अवनमन कोण `theta` व `phi` हैं। यदि `tan theta = 4/3` तथा `tan phi =5/2`, तब चिमनियों की चोटियों के मध्य दूरी है
View Solutionअन्तराल `[0,2pi]` में स्थित, समीकरण tan x + sec x =2cos x के हलों की संख्या है
View Solutionझील के तल से a मी ऊँचाई पर स्थित बादल का उन्नयन कोण a है तथा इसके प्रतिबिम्ब का अवनमन कोण B है, बादल की ऊँचाई है
View Solutionयदि समीकरण `5cos theta+ 4sin theta = 3` के मूल `alpha` तथा `beta` हैं, तब `cos (alpha +beta)` का मान है
View Solutionr त्रिज्या का गोलाकार गुब्बारा पर्यवेक्षक की आँख पर α कोण बनाता है। • यदि गुब्बारे के केन्द्र का उन्नयन कोण β है, तब गुब्बारे के केन्द्र की ऊँचाई है
View Solutionयदि `cos 5 theta = P cos theta -20 cos^3theta + Q cos^(5)theta+R` तब P+Q+ R का मान है
View Solutionयदि `a le sin^(-1) x + cos^(-1) x + tan^(-1) x le b`, तो
View Solution`Delta ABC` में, यदि `(cosA)/a=(cosB)/b=(cosC)/c` तब त्रिभुज है
View Solutionसमीकरण `tan^(-1)(x + 1) + tan^(-1) (x - 1) = tan^(-1)(8/31)` का हल है
View Solution`cos^(-1)xsqrt3+cos^(-1)x=pi/2` का हल है ।
View Solutionयदि `x =cos^(-1)(cos4). y = sin^(-1)(sin 3)`, तब निम्न में से कौन-सा प्रतिबन्ध सन्तुष्ट होता है?
View Solutionयदि `DeltaABC` का क्षेत्रफल `lamda` है, तब `a^2 sin2B + b^2 sin2A` का मान है
View Solutionयदि `|x|le1`, तब `2tan^(-1)x+sin^(-1)""(2x)/(1-x^(2))` बराबर है
View Solution`cos^(-1){1/sqrt2(cos""(7pi)/5 -sin""(7pi)/5)}` बराबर है।
View Solutionयदि `a, b, in R` , तब `sec^(2) theta = (4ab)/((a+b)^2)` सत्य है, यदि
View Solution`DeltaABC` में, यदि `R /rle 2` तब त्रिभुज है
View Solutionयदि `cot^(2)x + cosecx -a=0` का कम-से-कम एक हल है, तब a के सभी मानों का समुच्चय है
View Solutionयदि `f( theta , alpha ) = 2 sin^(2) theta + 4 cos( theta + alpha ) sin thetasinalpha + cos 2 ( theta + alpha), cos x = 0` का व्यापक हल `x = (2n + 1)""pi/2` है, जहाँ, `n inI` तथा `sin x = 0` का व्यापक हल `x =npi` है, जहाँ `n inI`
`f(pi/3,pi/4)` का मान है
View Solutionयदि `f( theta , alpha ) = 2 sin^(2) theta + 4 cos( theta + alpha ) sin thetasinalpha + cos 2 ( theta + alpha) ,cos x = 0` का व्यापक हल `x = (2n + 1)""pi/2` है, जहाँ, `n inI` तथा `sin x = 0` का व्यापक हल `x =npi` है, जहाँ `n inI`
`f(pi/3,alpha)=0` का व्यापक हल है
View Solutionजब भी प्रतिलोम त्रिकोणमितीय फलन को परिभाषित किया जाता है, एक नए निकाय का निर्माण होता है, जहाँ सहप्रान्त पुन: परिभाषित हो चुका होता है, जो निम्न प्रकार है
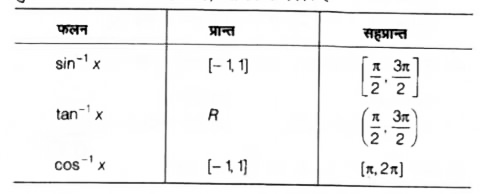
यदि `f(x) = 3sin^(-1) x -2cos^(-1) ` , तब f(x) है
View Solutionजब भी प्रतिलोम त्रिकोणमितीय फलन को परिभाषित किया जाता है, एक नए निकाय का निर्माण होता है, जहाँ सहप्रान्त पुन: परिभाषित हो चुका होता है, जो निम्न प्रकार है
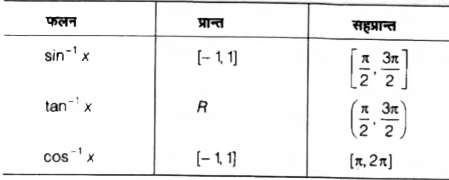
`(sin^(-1)x)^3 - (cos^(-1)x)^3` का न्यूनतम मान है
View Solutionवक्तव्य I यदि `1/2le x le 1` तब `cos^(-1)x sn^(-1)[x/2+(sqrt3-3x^2)/2]=pi/3`
वक्तव्य II `sin^(-1)(2xsqrt(1- x^2)) =2sin^(-1) x,` यदि `x in [-1/sqrt2,1/sqrt2]`
View Solutionमान लीजिए कि एक प्रेषक मैदान पर खड़ा है तथा टावर को देख रहा है, तब वह एक उन्नयन कोण बनाता है।
वक्तव्य I एक टावर बिन्दुओं A,B तथा C पर, जो सभी एक क्षैतिज रेखा पर स्थित हैं और टावर AB के पाद से होकर जाती है, क्रमशः `alpha,2alpha` तथा `3alpha` कोण अन्तरित करता है, तब `AB : BC = sin 3alpha. :sinalpha`
वक्तव्य || `DeltaABC ` में, यदि `a/(sinA)=b/sin=c/(sinC)` तब `DeltaABC` एक समबाहु त्रिभुज है।
View Solutionयदि कोई कोण समीकरण को सन्तुष्ट करता है, तब इसे उस समीकरण का हल कहते हैं।
वक्तव्य । अन्तराल `[0,2pi]` में समीकरणों `2 sin^2theta -cos 2 theta = 0` तथा `2cos^2 theta-3sintheta= 0` के दो हल हैं।
वक्तव्य ।I यदि `2cos^2theta-3sin theta =0` , तब `theta` तीसरे व चौथे चतुर्थांश में नहीं हो सकता।
View Solutionवक्तव्य I यदि `2sin ( theta/2) = sqrt(1+ sintheta)+sqrt(1-sin theta)`, तब `theta/2, 2npi+(pi)/4` और `2npi+ (3pi)/4` के बीच है।
वक्तव्य ॥ यदि `pi/4 le theta lt (3pi)/4` तब `sin ""theta/2 gt0`
View Solution
बहुविकल्पीय प्रश्न questions and complete solutions for chapter यूनिट टेस्ट 3 (त्रिकोणमिति ) of ARIHANT MATHS (HINDI) of Class 12