Complete Solutions to प्रश्नावली स्तर-1 of chapter सरल रेखा of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सरल रेखा |
| ARIHANT HINDI | प्रश्नावली स्तर-1 |
| Number Of Questions | 67 |
| Academic Year | 2023-24 |
सरल रेखा के लिए कितने ज्यामितीय प्राचलन होने चाहिए?
View Solutionउस रेखा की प्रवणता बताइए जो अक्षों पर समान लम्बाई के अन्त:खण्ड काटती है
View Solutionयदि रेखा `(x)/(a)+(y)/(b)=1` बिन्दुओं (2, -3) तथा (4, -5), से होकर गुजरती है, तब (a, b) है
View Solutionउन रेखाओं के समीकरण बताओं जोकि बिन्दु (3, -2) से होकर गुजरती है तथा रेखा `sqrt3 x + y =1` से इसका झुकाव `60^(@)` है
View Solutiony-अक्ष की ऋणात्मक दिशा में अन्त:खण्ड 2 काटने वाले तथा x-अक्ष की धनात्मक दिशा से `30^(@)` का कोण बनाने वाली सरल रेखा का समीकरण है
View Solutionसंलग्न चित्र में अपवर्तित किरण की समीकरण है
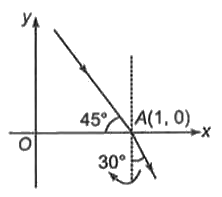
View Solutionबिन्दुओं (2, 3) तथा (3, -1) को मिलाने वाली रेखा के लम्बवत् तथा बिन्दु (5, 2) से होकर गुजरने वाली रेखा का समीकरण है,
View Solutionसारणिक `|[x, y, 1], [x_(1), y_(1), 1], [x_(2), y_(2), 1]| = 0` निरूपित करता है
View Solutionरेखा 3x +4y= 7 के समान्तर तथा रेखाओं 2x+ y=5 तथा x + 3y+8=0 के प्रतिच्छेदन बिन्दु से होकर गुजरने वाली रेखा का समीकरण है
View Solutionयदि निर्देशांक अक्षों के बीच किसी रेखा का अन्त:खण्ड बिन्दु (-5, 4) द्वारा 1:2, के अनुपात में विभाजित किया जाता है, तो रेखा का समीकरण है
View Solutionयदि समीकरण `x cos theta+ y sin theta=p`, रेखा `sqrt3 x + y+2 =0` का अभिलम्ब रूप है, तब `theta` व p का मान होगा
View Solutionएक सरल रेखा जिसके अक्षों पर अन्त:खण्डों का योग, अन्त:खण्डों के गुणनफल का आधा है, किस बिन्दु से होकर जाती है?
View Solutionरेखाओं x -y+1=0 तथा 2x -3y + 5 = 0 के प्रतिच्छेदन बिन्दु से होकर जाने वाली रेखा का समीकरण ज्ञात करो, जोकि बिन्दु (3, 2) से `(7)/(5)` दूरी पर स्थित है,
View Solutionयदि अशून्य संख्याएँ a, b, c हरात्मक श्रेणी में हैं, तब सरल रेखा `(x)/(a)+(y)/(b)+(1)/(c)= 0` सदैव एक निश्चित बिन्दु से गुजरती है, है
View Solutionरेखा y = x के लम्बवत् तथा बिन्दु (3, 2) से जाने वाली रेखा का समीकरण है
View Solutionयदि अक्षों के बीच अन्त: खण्डित किसी रेखा के भाग का मध्य-बिन्दु (3, 2) है, तो रेखा का समीकरण होगा
View Solutionयदि सरल रेखा ax+ by+ c= 0 सदैव (1, -2) से होकर जाती है, तब a, b, c हैं
View Solutionरेखाओं 3x + 4y+ 2 = 0 तथा 3x +4y+ 5 = 0 के बीच की दूरी को रेखा 3x +4y-5 = 0 निम्न में से किस अनुपात में बाँटती है?
View Solutionएक सरल रेखा P(1, 2) से होकर इस प्रकार जाती है कि निर्देशांकों के बीच इसका अन्त:खण्ड P पर समद्विभाजित होता है। सरल रेखा की समीकरण है
View Solution-2 प्रवणता वाली रेखा जोकि x-अक्ष को मूलबिन्दु से 3 इकाई बाईं ओर प्रतिच्छेद करती है
View Solutionबिन्दु (2, 2) से होकर जाने वाली रेखा का समीकरण ज्ञात कीजिए जिसके द्वारा अक्षों से कटे अन्त:खण्डों का योग 9 है।
View Solutionबिन्दुओं `(h, 3)` और `(4, 1)` से जाने वाली रेखा, `7x-9y - 19 = 0` को समकोण पर प्रतिच्छेदित करती है। `h` का मान ज्ञात कीजिए।
View Solutionउन रेखाओं के समीकरण ज्ञात कीजिए जिनके अक्षों से कटे अन्त:खण्डों का योग और गुणनफल क्रमश: 1 और -6 हैं
View Solutionरेखाओं `y = (2 - sqrt3)(x+ 5)` तथा `y = (2 + sqrt3)(x - 7)` के मध्य का कोण होगा
View Solutionबिन्दु (-3, 6) तथा बिन्दुओं (4, -5) तथा (-2, 9) को जोड़ने वाली रेखा के मध्य-बिन्दु से जाने वाली रेखा का झुकाव है
View Solutionरेखाओं `sqrt3x + y = 1` तथा `x + sqrt3y = 1` के बीच का कोण होगा
View Solutionरेखाओं 5x+3y-7 = 0 व 15x+9y +14 = 0 के बीच की दूरी हैं
View Solutionएक वर्ग जिसका क्षेत्रफल 25 वर्ग इकाई है, की दो भुजाएँ `3x + 4y =k_(1)` व `3x + 4y = k_(2)` हैं, तब `|k_(1) - k_(2)|` का मान है
View Solutionत्रिभुज के दो शीर्ष (6, -1) व (-2, 3) हैं। यदि त्रिभुज का लम्बकेन्द्र मूलबिन्दु पर है, तब तीसरे शीर्ष के निर्देशांक हैं
View Solutionशीर्षों (0, 0), (3, 4) व (4, 0) वाले त्रिभुज का लम्बकेन्द्र है
View Solutionरेखाओं y-x+ 7 = 0 व y+2x-2 = 0 के प्रतिच्छेदन बिन्दुओं को मूलबिन्दु से मिलाने वाली सरल रेखा का समीकरण है
View Solutionरेखाओं x + y = 1 तथा xy = 0 द्वारा बने त्रिभुज का लम्बकेन्द्र है
View Solutionमाना `Delta`PQR जिसके शीर्ष P(2, 2), Q (6, -1) व R(7, 3) है, की माध्यिका PS है। PS के समान्तर तथा बिन्दु (1, -1) से होकर जाने वाली रेखा का समीकरण है
View Solutionरेखा `sqrt3 sin theta+2 cos theta =(4)/(r)` के लम्बवत् तथा बिन्दु (-1, `(pi)/(2)`) से होकर जाने वाली रेखा का समीकरण है
View Solutionएक रेखा (1, 0) तथा (2, 3) बिन्दुओं को मिलाने वाली रेखाखण्ड पर लम्ब है तथा उसको 1:n के अनुपात में विभाजित करती है। रेखा का समीकरण ज्ञात कीजिए।
View Solutionसमद्विबाहु समकोण त्रिभुज की किसी एक भुजा का समीकरण ज्ञात कीजिए जिसका कर्ण 3x + 4y = 4 द्वारा दिया गया है तथा कर्ण के विपरीत शीर्ष के निर्देशांक (2, 2) हैं
View Solutionकिस दिशा में एक रेखा को बिन्दु (1, 2) से खींचना चाहिए, ताकि इस रेखा की रेखा x + y = 4 के साथ प्रतिच्छेद बिन्दु की दूरी `(sqrt6)/(3)` हो
View Solutionबिन्दु `(1, 0)` से जाने वाली एवं मूलबिन्दु से `(sqrt3)/(2)` की दूरी पर स्थित रेखाओं के समीकरण हैं
View Solutionरेखाओं 2x - 8y + 5 = 0 तथा 3x + 4y=0 के प्रतिच्छेद बिन्दु की रेखा 5x-2y=0 से दूरी है
View Solutionबिन्दु (2, 3) से रेखा y = 3x + 4 पर खींचे गए लम्ब के पाद बिन्दु के निर्देशांक हैं
View Solutionरेखाओं 4x + 3y+10 = 0, 5x - 12y+26 = 0 व 7x+24y-50 = 0 से समदूरस्थ बिन्दु है
View Solutionरेखा `y = x tan alpha + c`, जहाँ `c gt 0` पर बिन्दु (`a cos alpha, asin alpha`) से डाले गए लम्ब की लम्बाई है
View Solutionरेखा x-2y=1 के समान्तर, रेखा 2x+3y-14 = 0 से बिन्दु (3, 5) की दूरी है
View Solutionयदि समीकरण `t^(2) + lambda t + 1 = 0` के मूल `t_(1)` व `t_(2)` हैं, जहाँ `lambda` एक अचर है। तब, बिन्दुओं `(at_(1)^(2), 2at_(1))` व `(at_(2)^(2), 2at_(2))` को मिलाने वाली रेखा सदैव किस बिन्दु से होकर जाती है?
View Solutionएक रेखा x-अक्ष व y-अक्ष पर शून्य अन्त:खण्ड काटती है तथा यह दूसरी रेखा CD, 3x +4y+6 = 0 के लम्बवत् है। रेखा AB का समीकरण निम्न है
View Solutionरेखाओं 2x-3y+4 = 0 व 3x+4y-5 = 0 के प्रतिच्छेदन बिन्दु से जाने वाली तथा रेखा 6x-7y+3 = 0 के लम्बवत् रेखा का समीकरण निम्न है
View Solutionयदि रेखाओं x = a +m, y= -2 तथा y = mc संगामी हैं। तब, |a| का न्यूनतम मान है
View Solutionरेखाओं x-2y=1 तथा x+3y =2 के प्रतिच्छेदन बिन्दु से जाने वाली तथा रेखा 3x+4y=0 के समान्तर रेखा का समीकरण है
View Solutionसरल रेखाएँ ax+ by+c=0, bx+ cy+ a=0 तथा cx+ ay + b=0 (`a != b != c`) संगामी हैं, यदि
View Solutionसरल रेखाओं `(x+2y) +lambda(3x+2y+1) =0` व `(x-2y) +mu(x-y+1) = 0` के कुल की सरल रेखा का समीकरण है
View Solutionसरल रेखा `(x)/(a)-(x)/(b)=1`, x-अक्ष को बिन्दु P पर काटती है। इस रेखा के लम्बवत् P से जाने वाली सरल रेखा का समीकरण है
View Solutionरेखा y = 3x - 1 के समान्तर तथा बिन्दु (1, 2) से होकर जाने वाली रेखा का समीकरण है
View Solutionरेखाओं x=0, y=0, x=1 तथा y=1 से बने वर्ग के विकर्णों के समीकरण हैं
View Solutionएक रेखा, रेखा 3x + y = 3 के लम्बवत् तथा बिन्दु (2, 2) से होकर गुजरती है। इसकी y-अक्ष का अन्त:खण्ड है
View Solutionत्रिभुज की भुजाएँ x-3y = 0, 4x+3y =5 व 3x+ y= 0 है। रेखा 3x-4y=0 निम्न में से किस बिन्दु से होकर जाती है?
View Solutionरेखाएँ `x+ y = 0, 3x+ y = 4 व x+ 3y=4` एक त्रिभुज बनाती हैं, जो है
View Solution`DeltaABC` की भुजाओं AB और AC के लम्ब अर्द्धकों के समीकरण क्रमशः `x-y+5=0` और `x+2y=0` हैं। यदि बिन्दु A के निर्देशांक (1, -2) है, तो रेखा BC का समीकरण ज्ञात कीजिए।
View Solutionरेखाएँ 3x+4y = 5, 5x+4y = 4 व `lambdax+4y= 6` संगामी हैं, तब `lambda` का मान है
View Solutionरेखाएँ 2x+ y =1 व 2x+ y = 7 हैं
View Solutionएक चर बिन्दु P(x, y) तथा बिन्दुओं (1, 5), (3, – 7) द्वारा बने त्रिभुज का क्षेत्रफल 21 वर्ग इकाई है। बिन्दु P का बिन्दुपथ है।
View Solutionरेखाओं 3x-4y+ 7 = 0 व 12x+ 5y-2 = 0 के बीच के न्यून कोण के समद्विभाजक का समीकरण है
View Solutionरेखाओं |x|=|y| के बीच के कोणों के समद्विभाजकों के समीकरण हैं
View Solutionरेखा `x + y = 2` पर बिन्दु `(0, 0)` से डाले गये लम्ब के पाद बिन्दु के निर्देशांक हैं:
View Solutionबिन्दु (3, 2) से होकर जाने वाली रेखा का समीकरण, जोकि रेखा x-2y= 3 से `45^(@)` का कोण बनाती है, है
View Solutionबिन्दु (1, 2) से होकर जाने वाली एक प्रकाश किरण x-अक्ष के बिन्दु A से परिवर्तित होती है और परावर्तित किरण बिन्दु (5, 3) से होकर जाती है। A के निर्देशांक हैं
View Solutionबिन्दु (3, 4) से दो सरल रेखाएँ खींची जाती हैं। जिनमें से प्रत्येक रेखा x-y = 2 के साथ `45^(@)` का कोण बनाती है, तब इन रेखाओं से बने त्रिभुज का क्षेत्रफल है
View Solutionरेखा `(x -2y + 3) + lambda(2x - 3y + 4) = 0`, (`lambda in R`) में बिन्दु (2, 3) की प्रतिबिंब का समीकरण है
View Solution
प्रश्नावली स्तर-1 questions and complete solutions for chapter सरल रेखा of ARIHANT MATHS (HINDI) of Class 12