Complete Solutions to Exercise (Questions Asked In Previous 13 Years Exam) of chapter DEFINITE INTEGRAL of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | DEFINITE INTEGRAL |
| ARIHANT MATHS | Exercise (Questions Asked In Previous 13 Years Exam) |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
Evaluate: `int_(-pi//2)^(pi//2)(x^2cosx)/(1+e^x)dx`
View SolutionThe total number for distinct `x epsilon[0,1]` for which `int_(0)^(x)(t^(2))/(1+t^(4))dt=2x-1` is __________.
View SolutionLet `f(x)=7tan^8x+7tan^6x-3tan^4x-3tan^2x` for all `x in (-pi/2,pi/2)` . Then the correct expression (s) is (are) (a) `int_0^(pi/4)xf(x)dx=1/(12)` (b) `int_0^(pi/4)f(x)dx=0` (c) `int_0^(pi/4)xf(x)=1/6` (d) `int_0^(pi/4)f(x)dx=1/(12)`
View SolutionLet `f'(x)=(192x^(3))/(2+sin^(4)pix)` for all `x epsilonR` with `f(1/2)=0`. If `mle int_(1//2)^(1)f(x)dxleM`, then the possible values of `m` and `M` are
View SolutionThe option(s) with the values of `aa n dL` that satisfy the following equation is (are) `(int_0 ^(4pi)e^t(sin^6a t+cos^4at)dt)/(int_0^pie^t(sin^6at+cos^4a t)dt)=L` (a)`a=2,L=(e^(4pi)-1)/(e^(pi)-1)` (b) `a=2,L=(e^(4pi)+1)/(e^(pi)+1)` `a=4,L=(e^(4pi)-1)/(e^(pi)-1)` (d) `a=4,L=(e^(4pi)+1)/(e^(pi)+1)`
View SolutionLet `F:RtoR` be a thrice differntiable function. Suppose that `F(1)=0,F(3)=-4` and `F'(x)lt0` for all `x epsilon(1//2,3)`. Let `f(x)=xF(x)` for all `x inR`. Then the correct statement(s) is (are)
View SolutionLet F : R `to` R be a thrice differentiable function . Suppose that `F(1)=0,F(3)=-4 and F(x) lt 0 ` for all `x in (1,3)`. `f(x) = x F(x)` for all `x inR`.
If `int_(1)^(3)x^(2)F'(x)dx=-12 andint_(1)^(3)x^(3)F'' (x)dx =40`, then the correct expression (s) is //are
View SolutionLet `f:RtoR` be a function defined by `f(x)={([x],xle2),(0,xgt2):}` where `[x]` is th greatest integer less than or equal to `x`. If `I=int_(-1)^(2)(xf(x^(2)))/(2+f(x+1))dx`, then the value of `(4I-1)` is
View SolutionIf `alpha=int_0^1(e^(9x+3tan^((-1)x)))((12+9x^2)/(1+x^2))dxw h e r etan^(-1)` takes only principal values, then the value of `((log)_e|1+alpha|-(3pi)/4)i s`
View SolutionThe integral `overset(pi//2)underset(pi//4)int (2 cosecx)^(17)dx` is equal to
View SolutionLet `f:[0,2]vecR` be a function which is continuous on [0,2] and is differentiable on (0,2) with `f(0)=1` `L e t :F(x)=int_0^(x^2)f(sqrt(t))dtforx in [0,2]dotIfF^(prime)(x)=f^(prime)(x)` . for all `x in (0,2),` then `F(2)` equals `e^2-1` (b) `e^4-1` `e-1` (d) `e^4`
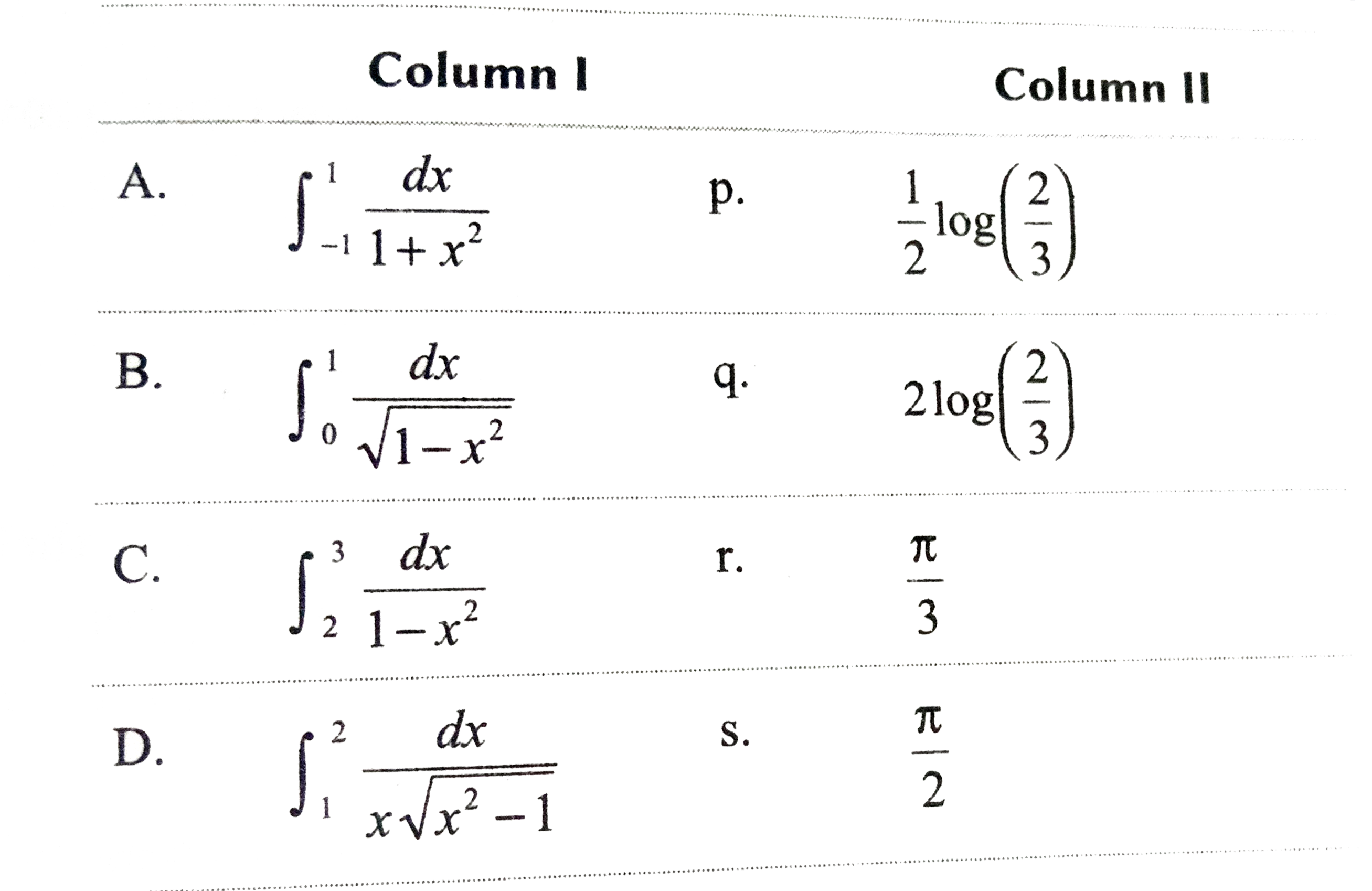
View SolutionMatch the conditions/ expressions in Column I with statement in Column II
View SolutionMatch List I with List II and select the correct answer using codes given below the lists
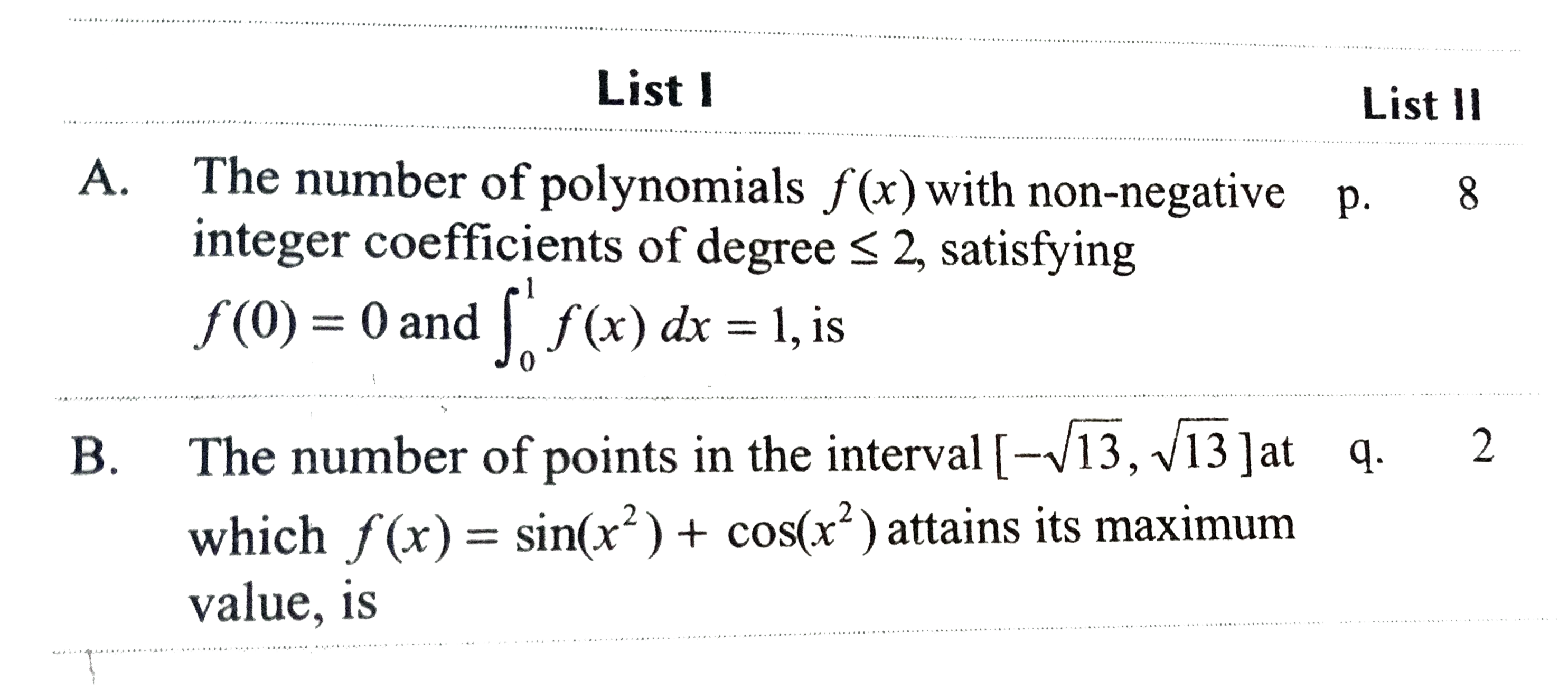
View SolutionThe value of `int_0^1 4x^3{(d^2)/(dx^2)(1-x^2)^5}dx` is
View SolutionThe value of the integral `int_(-pi//2)^(pi//2) (x^(2) + log" (pi-x)/(pi+x)) cos x dx `
View SolutionThe valued of `int_(sqrt(In2))^(sqrt(In3)) (x sinx^(2))/(sinx^(2)+sin(In 6-x^(2)))dx` is
View SolutionLet `f:[1,oo]` be a differentiable function such that `f(1)=2.` If `int_1^xf(t)dt=3xf(x)-x^3` for all `xgeq1,` then the value of `f(2)` is
View SolutionThe value of `int_(0)^(1)(x^(4)(1-x)^(4))/(1+x^(4))dx` is (are)
View SolutionFor `a epsilonR` (the set of all real numbers) `a!=-1, lim_(n to oo) ((1^(a)+2^(a)+………+n^(a)))/((n+1)^(a-1)[(na+1)+(n+2)+………..+(na+n)])=1/60`
Then `a=`
View SolutionLet `f:[0,1]toR` (the set of all real numbers ) be a function. Suppose the function f is twice differentiable,f(0)=f(1)=0 and satisfies
`f''(x)-2f'(x)+f(x)gee^(x),x in [0,1]` Consider the statements.
I. There exists some `x in R` such that, `f(x)+2x=2(1+x^(2))`
(II) There exists some `x in R` such that, 2f(x)+1=2x(1+x)
View SolutionWhich of the following is true?
View SolutionFor any real number `x ,l e t[x]` denote the largest integer less than or equal to `x ,L e tf` be a real-valued function defined on the interval `[-10 , 10]` be `f(x)={x-[x],if[x]i sod d1+[x]-x ,if[x]i se v e n` Then the value of `(pi^2)/(10)int_(-10)^(10)f(x)cospixdxi s____`
View SolutionLet `f` be a non-negative function defined on the interval `[0,1]`. If `int_0^xsqrt(1-(f^(prime)(t))^2)dt=int_0^xf(t)dt ,0lt=xlt=1,a n d \ f(0)=0`, then
View SolutionIf `int_(n)=int_(-pi)^(pi)(sin nx)/((1+pi^(x))sinx) dx, n=0,1,2,……….` then
View SolutionLet `S_(n)=sum_(k=1)^(n)n/(n^(2)+kn+k^(2))` and `T_(n)=sum_(k=0)^(n-1)n/(n^(2)+kn+k^(2))` for `n=1,2,3,`………. Then
View SolutionThen integral `int_(pi//4)^((3pi)/4) (dx)/(1+cosx)` is equal to
View Solution`"Let " I_(n)=int tan^(n)x dx,(n gt 1). I_(4)+I_(6)=a tan^(5)x+bx^(5)+C, " where C is a constant of integration, then the ordered pair (a,b) is equal to "`
View Solution`lim_(n -> oo) (((n+1)(n+2)(n+3).......2n) / n^(2n))^(1/n)`is equal to
View SolutionThe integral `int_(2)^(4)(logx^(2))/(logx^(2)+log(36-12x+x^(2))) dx` is equal to
View SolutionThe integral `int_(0)^(pi)sqrt(1+4"sin"^(2)x/2-4"sin"x/2)dx` is equals to (a)`pi-4` (b)`(2pi)/3-4-sqrt(3)` (c)`(2pi)/3-4-sqrt(3)` (d)`4sqrt(3)-4-(pi)/3`
View SolutionStatement I The value of the integral `int_(pi//6)^(pi//3) (dx)/(1+sqrt(tan x)) is pi/6` Statement II `int_(a)^(b) f(x) dx = int_(a)^(b) f(a+b-x)dx`
View SolutionThe intercepts on `x`- axis made by tangents to the curve, `y=int_(0)^(x)|t|dt, x epsilonR` which are parallel to the line `y=2x`, are equal to
View SolutionIf `g(x)=int_(0)^(x)cos^(4)t dt,` then `g(x+pi)` equals to (a)`(g(x))/(g(pi))` (b)`g(x)+g(pi)` (c)`g(x)-g(pi)` (d)`g(x).g(pi)`
View SolutionThe value of `int_(0)^(1)(8log(1+x))/(1+x^(2))dx` is
View SolutionFor `x epsilon(0,(5pi)/2)`, definite `f(x)=int_(0)^(x)sqrt(t) sin t dt`. Then `f` has
View SolutionLet `p(x)` be a function defined on R such that `lim_(xrarr infty) f (3x)/(f(x))=1,p'(x)=p'(1-x),"for all" x in [0,1],p(0)=1 and p(1)=41."Then" , int_(0)^(1)p(x) dx` equals
View Solution`int_(0)^(pi)[cos x] dx, [ ]` denotes the greatest integer function , is equal to
View SolutionLet `I=int_(0)^(1)(sinx)/(sqrtx) dx and f= int_(0)^(1)( cos x)/(sqrtx) dx`
Then , which one of the following is true ?
View Solution
Exercise (Questions Asked In Previous 13 Years Exam) questions and complete solutions for chapter DEFINITE INTEGRAL of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS DEFINITE INTEGRAL
- Definite intefral Exercise 1 : Single Option Correct Type Questions
- Example
- Exercise (Matching Type Questions)
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 4
- Exercise For Session 5
- Exercise For Session 6