Complete Solutions to Exercise of chapter GRAPHICAL TRANSFORMATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | GRAPHICAL TRANSFORMATIONS |
| ARIHANT MATHS | Exercise |
| Number Of Questions | 76 |
| Academic Year | 2023-24 |
Plot `y=|x| and y=|x|+2.`
View SolutionPlot `y=|x| and y=|x|-2.`
View SolutionPlot `y=e^(x),y=e^(x)+1 and y=e^(x)-1.`
View SolutionPlot `y=|x| and y=|x-2|`
View SolutionPlot `y=|x| and y=|x+2|`
View SolutionPlot `y=sin(x+(pi)/(4)) and y =sin(x-(pi)/(4))`.
View SolutionPlot `y=sinxa n dy=2sinxdot`
View SolutionPlot `y=sinx and y=(1)/(2)sinx`.
View SolutionPlot `y=sinxa n dy=sin2xdot`
View SolutionPlot `y=sinx and y=(1)/(2)sinx`.
View SolutionDraw the graph of `y=e^(-x),` when the graph of `y=e^(x)` is known.
View SolutionDraw graph of `y=log(-x),` when the graph of `y=log(x)` is given.
View SolutionDraw the graph of `y=-e^(x)` when the graph of `y=e^(x)` is known.
View SolutionDraw the graph of `y=-log(x)` when the graph of `y=logx` is known.
View SolutionDraw the graph of `y=|logx|` when the graph of `y=log(x)` is known.
View SolutionDraw the graph of `y=log|x|` when the graph of `y=log(x)` is known.
View SolutionDraw the graph of `y=||x|^(2)-2|x|-3|,` if `y=x^(2)-2x-3`
View SolutionDraw graph for `y=|x-1|.`
View SolutionDraw the graph for `|y|=(x-1)(x-2).`
View SolutionDraw the graph of `y=[x^(3)],`
when `-2^(1//3)le x le 2^(1//3)`
View SolutionDraw the graph of `y=[sinx].`
View SolutionDraw the curve `y=e^(x)`
View SolutionDraw the graph for `y=({x}-1)^(2)`.
View SolutionPlot `y=x+sinx.`
View SolutionPlot `y=|x|-2` and hence `f(x)=(1)/(|x|-2)`
View SolutionLet `f(x)={{:(x sin.(1)/(x)",",x ne0),(0",",x=0):}}` and `g(x)={{:(x^(2)sin.(1)/(x)",", x ne 0),(0",", x=0):}}`
Discuss the graph for f(x) and g(x), and evaluate the continuity and differentiabilityof f(x) and g(x).
View SolutionDraw graph for `y=max{2x, x^(2)}` and discuss the continuity and diffrentiablity.
View SolutionDraw the graph of `y=2-|x-1|`.
View SolutionLet `h(x) = min {x, x^2}`, for every real number of X. Then (A) h is continuous for all x (B) h is differentiable for all x (C) `h^'(x)` = 1, for all x > 1 (D) h is not differentiable at two values of x
View SolutionThe number of real solution of the equation `e^(x)+x=0,` is
View SolutionThe number of real solutions of the equation `log_(a)x=|x|,0 lt a lt 1`, is
View Solutionnumber of solution of the equation ` |x| = cos x`
View SolutionHow many roots does the following equation possess `3^(|x|)(|2-|x||)=1`?
View SolutionThe number of real solution of the equation
`x^(2)=1-|x-5|` is:
View SolutionNumber of solutions `2^(sin(|x|))=4^(|cosx|) in [-pi,pi]` is equal to
View SolutionNumber of roots of `|sin|x||=x+|x|"in"[-2pi,2pi]`, is
View SolutionThe equation `3^(x-1)+5^(x-1)=34` has
View SolutionNumber of solutions of the equation `cos[x]=e^(2x-1),x in [0,2pi]`, where[.] denotes the greatest integer function is
View SolutionLet `g(x)=sqrt(x-2k),AA2klt=x<2(k+1),` where `k in ` integer. Check whether `g(x)` is periodic or not.
View SolutionThe graph of f(x) is given below.
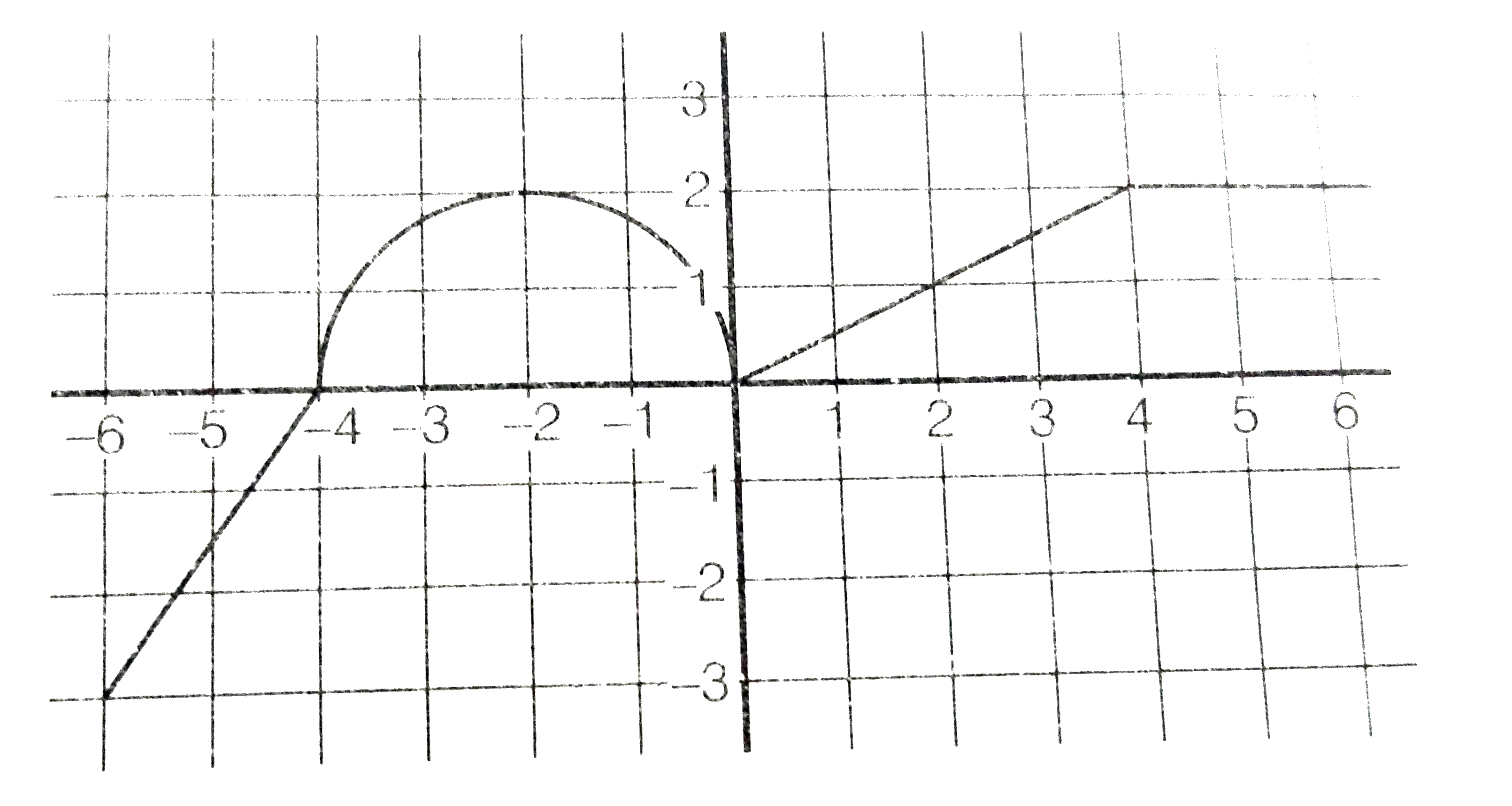
Then, (a) Graph of `-f(x)+2` is

View SolutionNumber of solutions of the equation, `[y+[y]]=2cosx` is: (where `y=1//3)[sinx+[sinx+[sinx]]]` and `[]=` greatest integer function) 0 (b) 1 (c) 2 (d) `oo`
View SolutionThe sum of roots of the equation `cos^(-1)(cosx)=[x],[dot]` denotes the greatest integer function, is `2pi+3` (b) `pi+3` (c) `pi-3` (d) 2`pi-3`
View SolutionSketch the graph of `y=log_(0.5)|x|.`
View SolutionSketch the graph of `y=||(1)/(x)|-3|`.
View SolutionFind the number of solutions of the equations `y=|sinx| and x^(2)+y^(2)=1.`
View SolutionFind the number of solutions of `4{x}=x+[x].`
View SolutionSketch the graph of `|sinx+(1)/(2)|.`
View SolutionSketch the graph of `y=(2^(x))/(2^(|x|))`
View SolutionSketch the region for `y=sin(x-[x])`.
View SolutionSketch the region for `|y|==sinx.`
View SolutionConsider the following function f whose graph is given below.
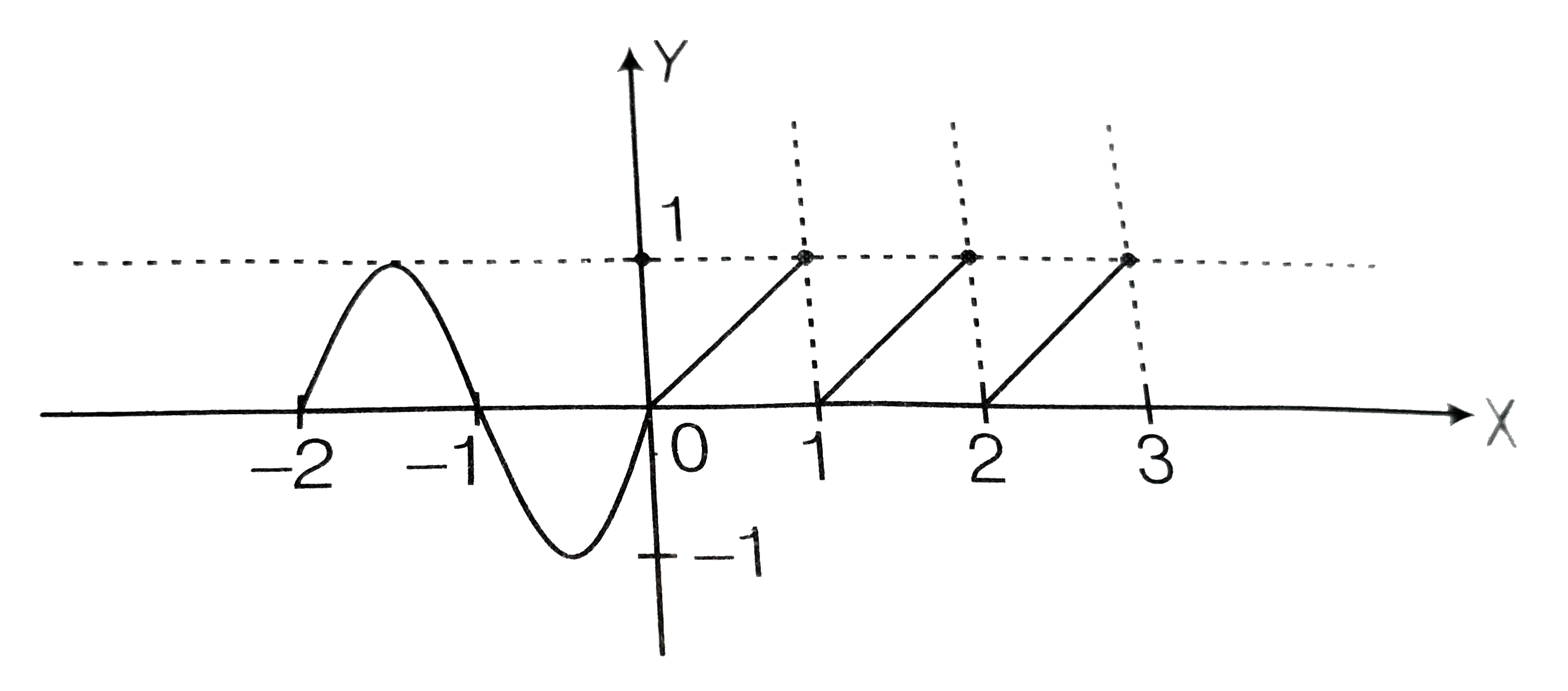
Draw the graph of following functions.
(a) `f(x)+1`
View SolutionConsider the following function f whose graph is given below.
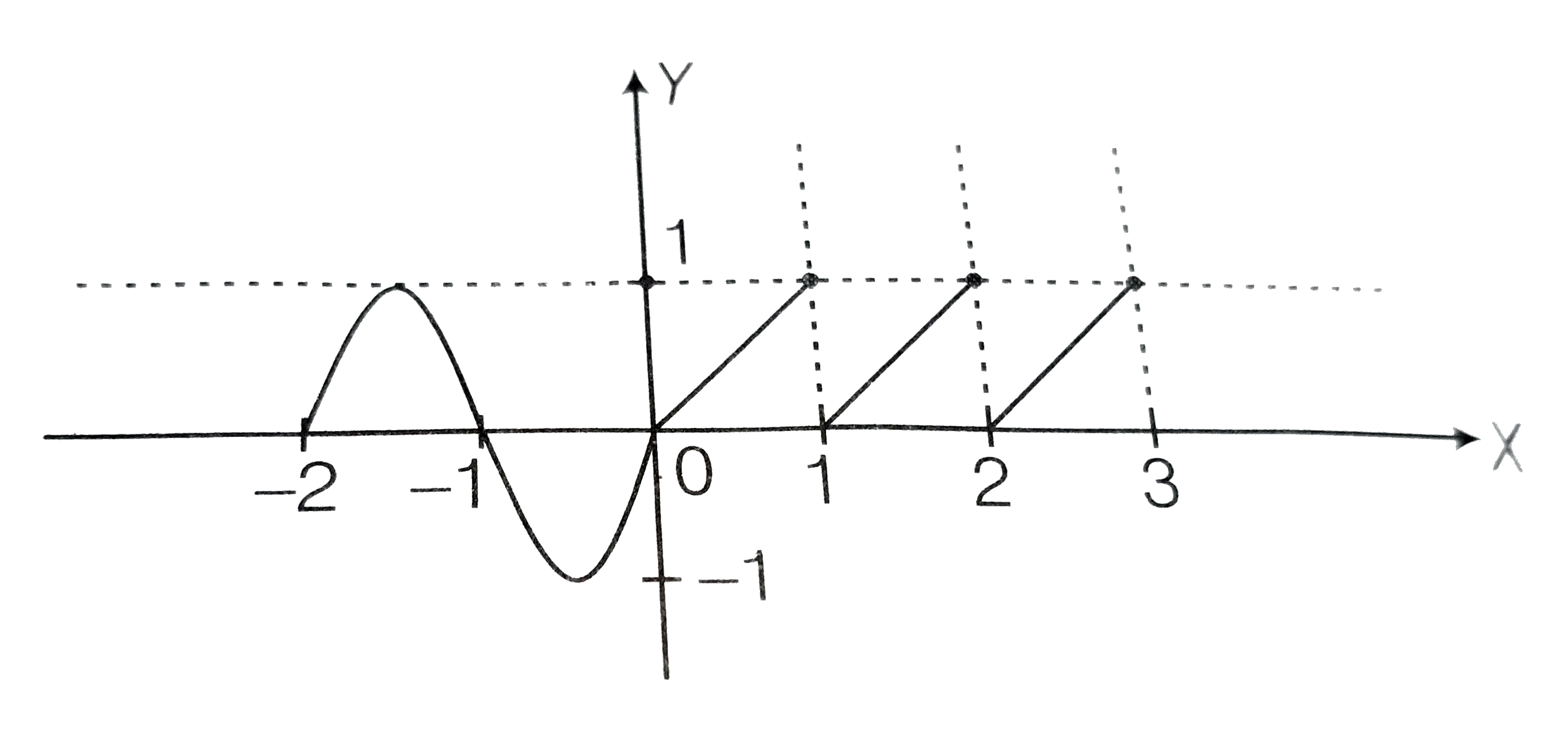
Draw the graph of following functions.
`f(x)-1`
View SolutionConsider the following function f whose graph is given below.
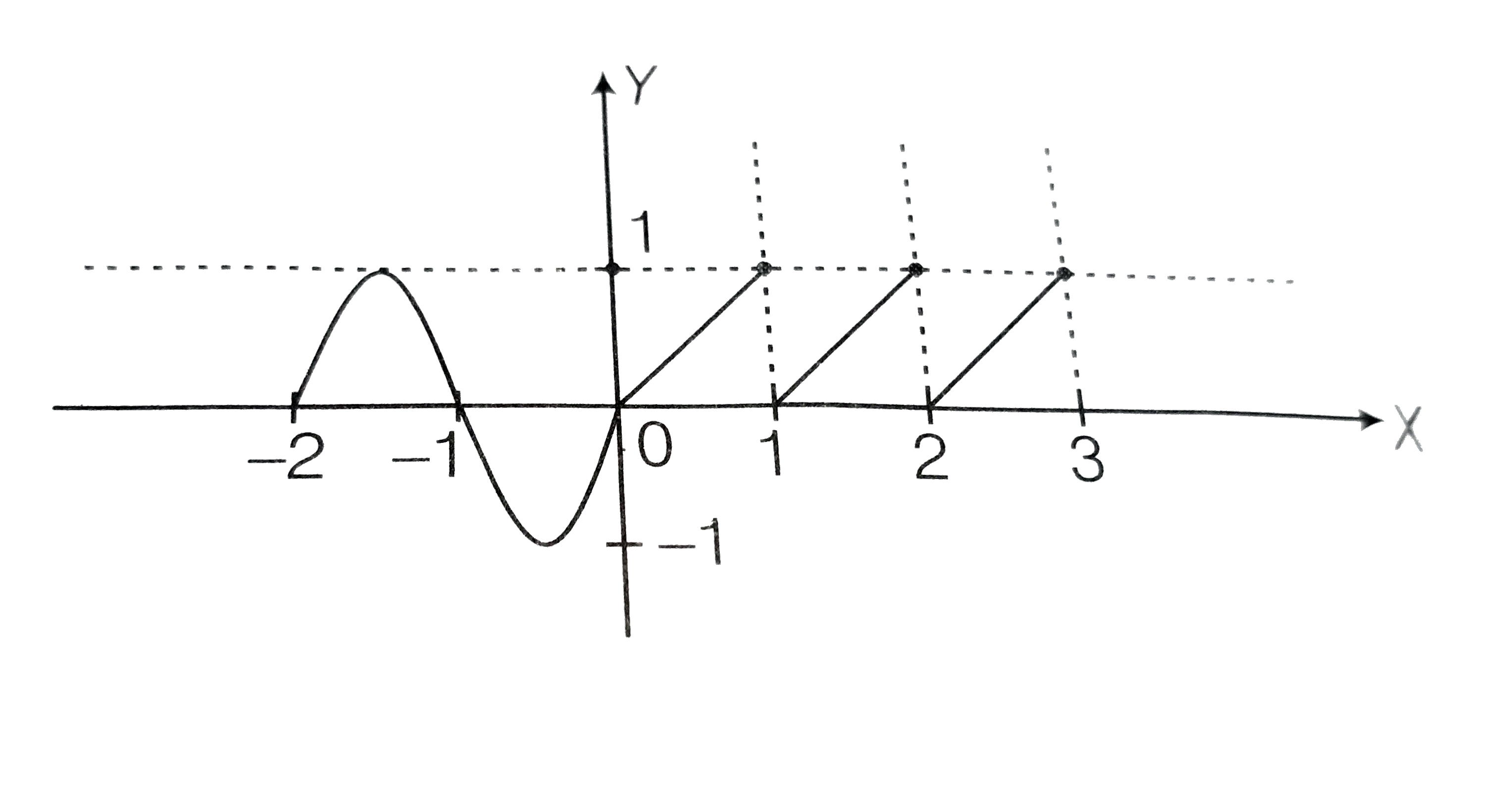
Draw the graph of following functions.
(c) `-f(x)`
View SolutionConsider the following function `f` whose graph is given below.
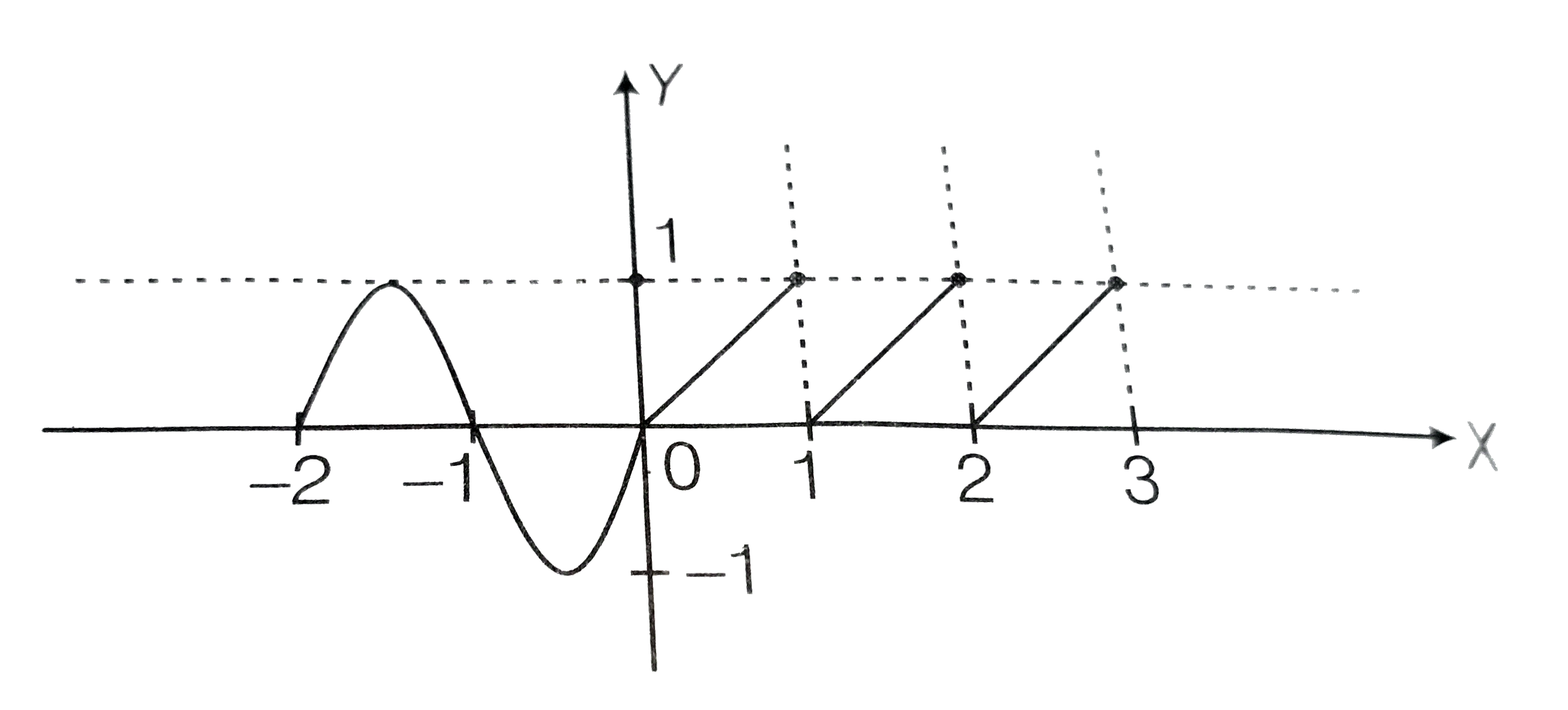
Draw the graph of `[f(x)]`
View SolutionConsider the following function f whose graph is given below.
Draw the graph of `f(-x)`
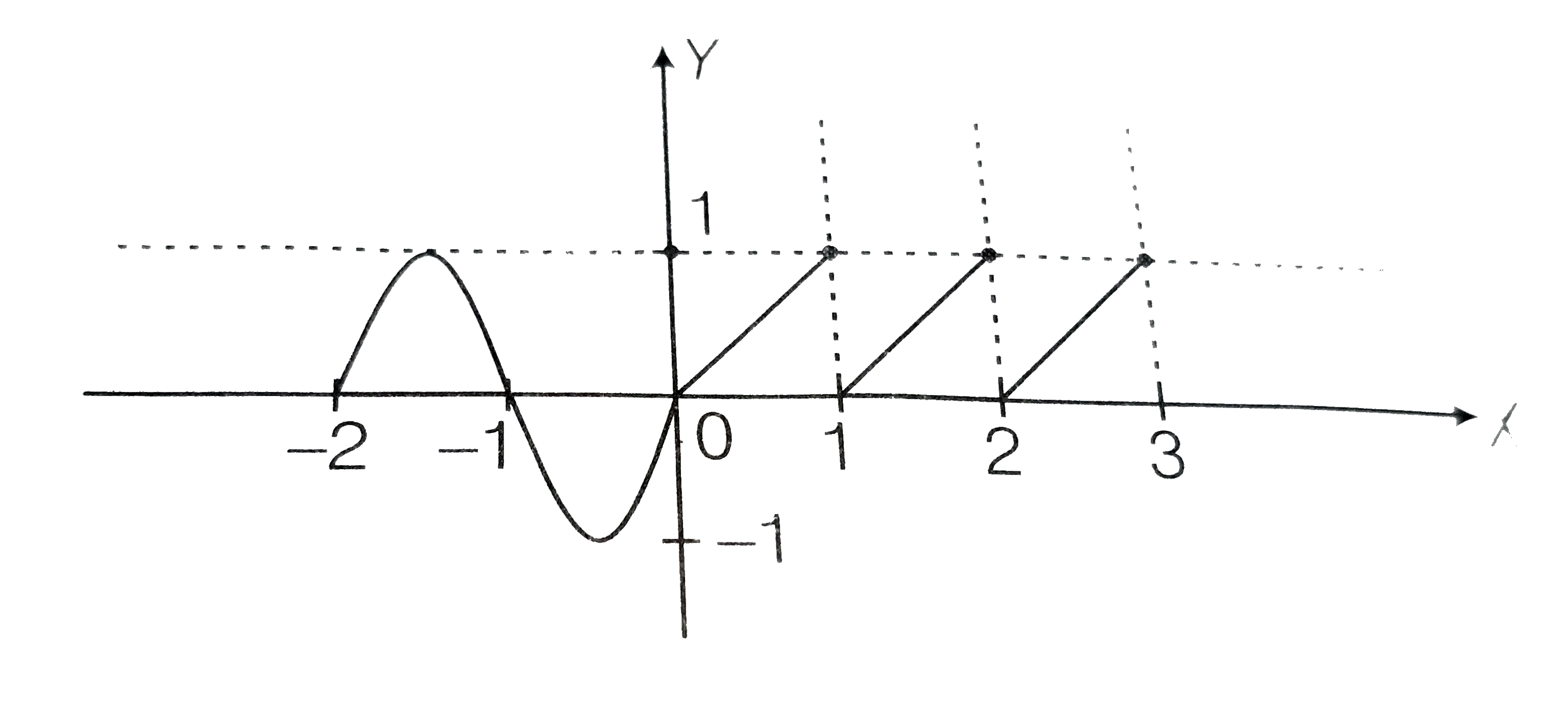
View SolutionConsider the following function f whose graph is given below.

Draw the graph of following functions.
(f) `f(|x|)`
View SolutionConsider the following function f whose graph is given below.
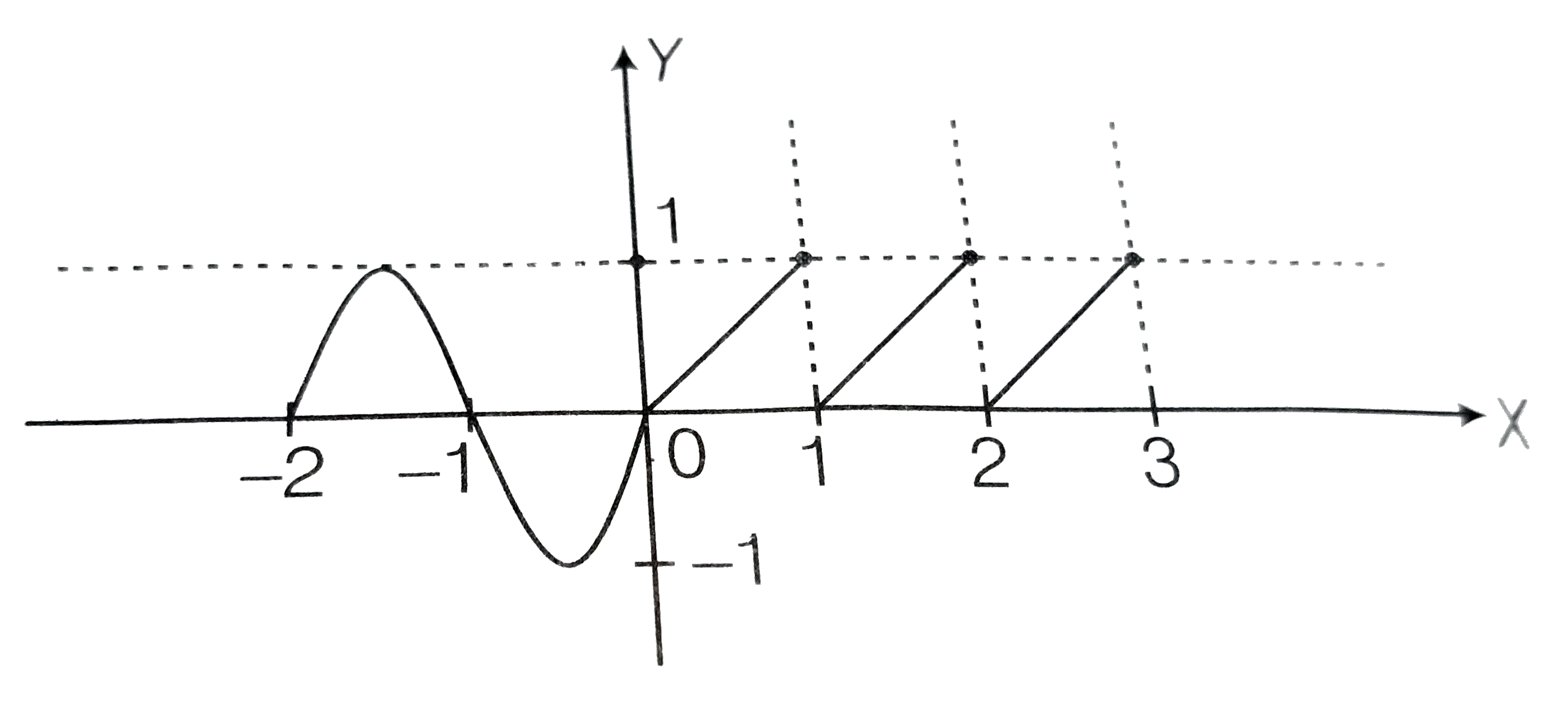
Draw the graph of following functions.
(g) `2f(x)`
View SolutionConsider the following function f whose graph is given below.

Draw the graph of following functions.
`f(2x)`
View SolutionConsider the following function `f` whose graph is given below.

Draw the graph of `[f(x)]`
View SolutionConsider the following function f whose graph is given below.
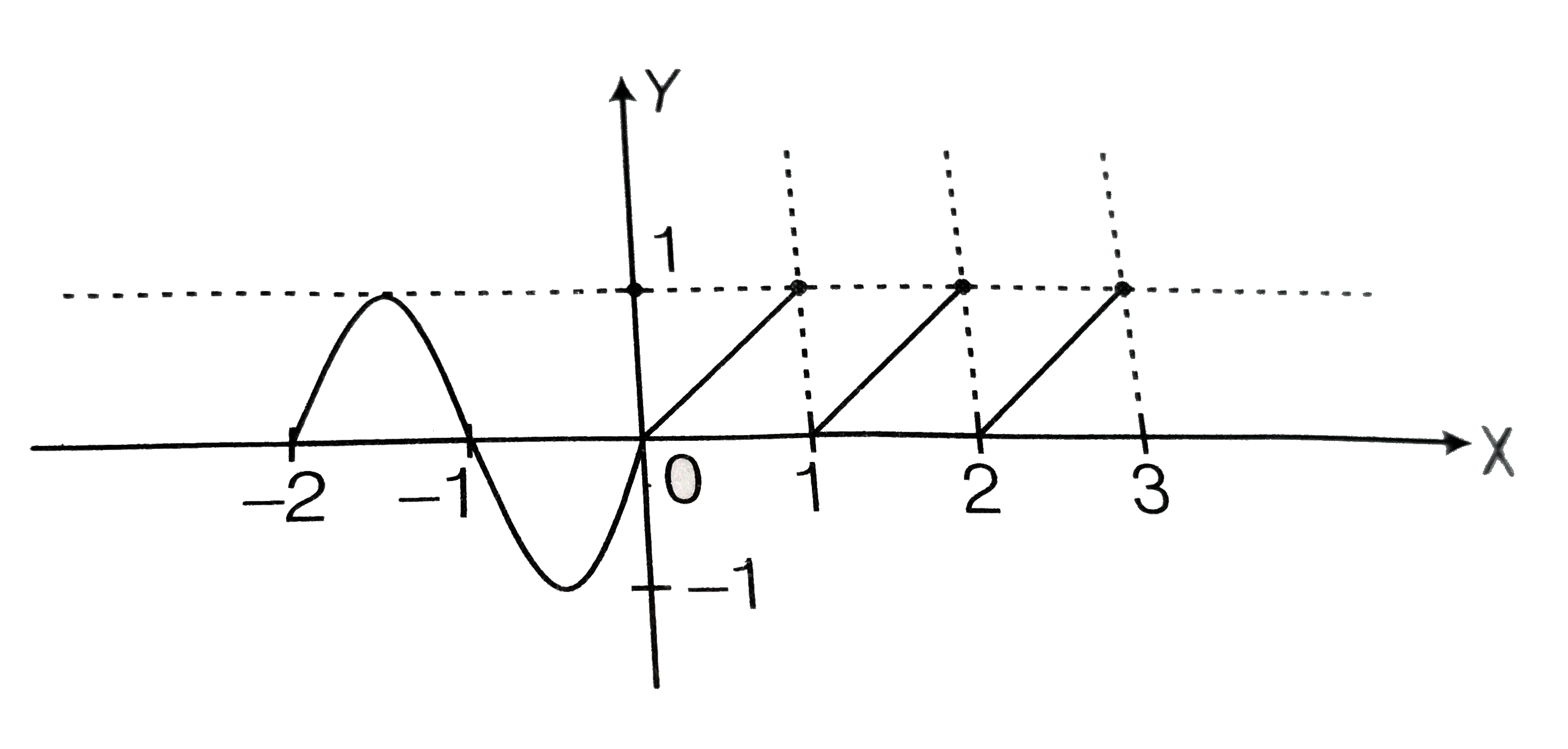
Draw the graph of following functions.
(g) `f(x-[x])`
View SolutionSketch the graph of `y = max (sinx, cosx), AA x in (-pi,(3pi)/(2)).`
View SolutionSketch the graph for `y=min{tanx, cotx}.`
View SolutionSketch the graph of `y=min{|x|,|x-1|,|x+1|}.`
View SolutionSketch the graph of `y=sin^(-1)x, AA x in [-1,1]`.
View SolutionSketch the graph for `y=cos^(-1)x, AA x in [-1, 1]`.
View SolutionSketch the graph for `y=tan^(-1)x, AA x in R.`
View SolutionSketch the graph for `y=sin^(-1)(sinx).`
View SolutionSketch the graph for `y=cos^(-1)(cosx).`
View SolutionDraw the graph of `y = tan^(-1)(tan x)`
View SolutionFind the value of x graphically which satisfy `|(x^(2))/(x-1)|le1.`
View SolutionFind `dy/dx if x=e^y`
View SolutionFind the values of x graphically which satisfy, `-1le[x]-x^(2)+4le2`, where `[.]` denotes the greatest integer function.
View SolutionFind the number of solutions of `2cos x=|sinx|` when `x in [0,4pi]`.
View SolutionSketch the curves
(i)`y=sqrt(x-[x])`
(where [.] denotes the greatest integer function).
View SolutionSketch the curves
(iii) `y=|[x]+sqrt(x-[x])|`
(where [.] denotes the greatest integer function).
(where [.] denotes the greatest integer function).
View SolutionSketch the curves
(iii) `y=|[x]+sqrt(x-[x])|`
(where [.] denotes the greatest integer function).
(where [.] denotes the greatest integer function).
View Solution
Exercise questions and complete solutions for chapter GRAPHICAL TRANSFORMATIONS of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS GRAPHICAL TRANSFORMATIONS
- Exercise
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 4