Complete Solutions to Example of chapter ELLIPSE of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | ELLIPSE |
| ARIHANT MATHS | Example |
| Number Of Questions | 4 |
| Academic Year | 2023-24 |
Find the locus of the points of the intersection of tangents to ellipse `x^(2)/a^(2)+y^(2)/b^(2)=1` which make an angle theta.
View SolutionProve that the locus of the middle points of normal chords of the ellipse `x^(2)/a^(2)+y^(2)/b^(2)=1` is the curve `(x^(2)/a^(2)+y^(2)/b^(2))(a^(6)/x^(2)+b^(6)/y^(2))=(A^(2)-B^(2))^(2)`
View SolutionMatch the following
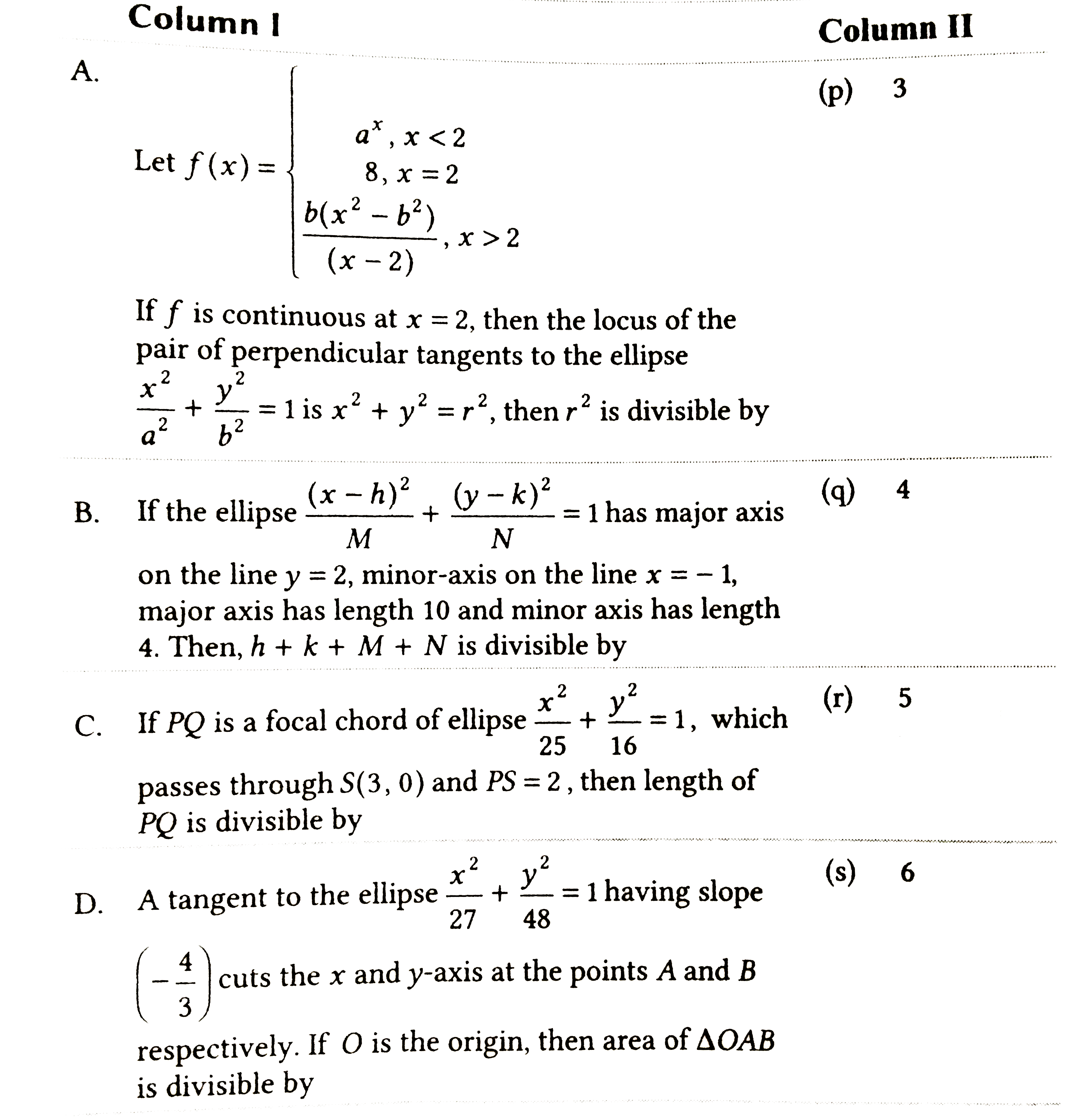
View SolutionFrom any point on the conic `(x^(2))/(a^(2))+(y^(2))/(b^(2))=4`. Tangents are drawn to the conic `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`. Prove that the normals at the points of contact meet on the conic
`a^(2)x^(2)+b^(2)y^(2)=(1)/(4)(a^(2)-b^(2))^(2)`.
View Solution
Example questions and complete solutions for chapter ELLIPSE of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS ELLIPSE
- Ellipse Exercise 5: Matching Type Questions
- Ellipse Exercise 7: Subjective Type Questions
- Example
- Examples
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3