Complete Solutions to Examples of chapter DETERMINANTS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | DETERMINANTS |
| ARIHANT MATHS | Examples |
| Number Of Questions | 73 |
| Academic Year | 2023-24 |
Find the value of the determinant
`|{:(1,2,4),(3,4,9),(2,-1,6):}|`
View SolutionIf `Delta=|{:(1,sintheta,1),(-sintheta,1,sintheta),(-1,-sintheta,1):}|"prove that" 2lt=Deltalt=4.`
View SolutionExpand `|{:(3,2,5),(9,-1,4),(2,3,-5):}|` by Sarrus rule.
View SolutionIf a,b,c,`in` R, find the number of real root of the equation `|{:(x,c,-b),(-c,x,a),(b,-a,x):}|`=0
View SolutionExpand `|{:(1,2,3),(4,6,2),(5,9,4):}|`
View SolutionFind the value of the determinant
`|{:(-1,2,1),(3+2sqrt(2),2+2sqrt(2),1),(3-2sqrt(2),2-2sqrt(2),1):}|`
View SolutionFind the determinants of minors of the determinant `|{:(1,2,3),(-4,3,6),(2,-7,9):}|`
View SolutionIf the value of a third order determinant is 11, find the value of the square of the determinat formed by the cofactors.
View SolutionEvaluate `|{:(13,16,19),(14,17,20),(15,18,21):}|`.
View SolutionProve that `|{:(alpha,beta,gamma),(theta,phi,psi),(lambda,mu,nu):}|=|{:(beta,mu,phi),(alpha,lambda,theta),(gamma,nu,psi):}|.`
View SolutionUsing properties of determinants, prove that `|b+c q+r y+z c+a r+p z+x c+b p+q x+y|=2\ |a p x b q y c r z|`
View SolutionSolve for x,
`|{:(4x,6x+2,8x+1),(6x+2,9x+3,12x),(8x+1,12x,16x+2):}|`=0
View SolutionUsing properties of determinants, prove that :
`|{:(a^(2)+1,ab,ac),(ba,b^(2)+1,bc),(ca,cb,c^(2)+1):}|=a^(2)+b^(2)+c^(2)+1`
View SolutionIf a,b, and c are all different and if
`|{:(a,a^(2),1+a^(3)),(b,b^(2),1+b^(3)),(c,c^(2),1+c^(3)):}|`=0 Prove that abc =-1.
View Solutionfind the larget value of a third- order determinant whose elements are 0 or 1.
View SolutionFind the largest value of a third order determinant whose elements are 0 or -1.
View SolutionShow that the value of a third order determinant whose all elements are 1 or -1 is an even number.
View SolutionEvaluate `|[1,2,3],[-2,3,2],[3,4,-4]|xx|[-2,1,3],[3,-2,1],[2,1,-2]|`. Using the concept of multiplication of determinants.
View SolutionIf `a x1 2+b y1 2+c z1 2=a x2 2+b y2 2+c z2 2=a x3 2+b y3 2+c z3 2=d ,a x2 3+b y_2y_3+c z_2z_3=a x_3x_1+b y_3y_1+c z_3z_1=a x_1x_2+b y_1y_2+c z_1z_2=f,` then prove that `|x_1y_1z_1x_2y_2z_2x_3y_3z_3|=(d-f){((d+2f))/(a b c)}^(1//2)`
View SolutionProve that `|{:(a_(1)alpha_(1)+b_(1)beta_(1),a_(1)alpha_(2)+b_(1)beta_(2),a_(1)alpha_(3)+b_(1)beta_(3)),(a_(2)alpha_(1)+b_(2)beta_(1),a_(2)alpha_(2)+b_(2)beta_(2),a_(2)alpha_(3)+b_(2)beta_(3)),(a_(3)alpha_(1)+b_(3)beta_(1),a_(3)alpha_(2)+b_(3)beta_(2),a_(3)alpha_(3)+b_(3)beta_(3)):}|`=0.
View SolutionProve that `|{:(2,,alpha+beta+gamma+delta,,alphabeta+gammadelta),(alpha+beta+gamma+delta,,2(alpha+beta)(gamma+delta),,alphabeta(gamma+delta)+gammadelta(alpha+beta)),(alphabeta+gammadelta,,alphabeta(gamma+delta)+gammadelta(alpha+beta),,2alphabetagammadelta):}|`
View SolutionFor all values of `A ,B ,Ca n dP ,Q ,R` show that `|"cos"(A-P)"cos"(A-Q)"cos"(A-R)"cos"(B-P)"cos"(B-Q)"cos"(B-R)"cos"(C-P)"cos"(C-Q)"cos"(C-R)|=0`
View SolutionIf `alpha,beta,gamma` are real numbers, then without expanding at any stage, show that `|1cos(beta-alpha)"cos"(gamma-alpha)"cos"(alpha-beta)1"cos"(gamma-beta)"cos"(alpha-gamma)"cos"(beta-gamma)1|=0`
View SolutionSolve the following system of equation by Cramer's rule.
x+y=4 and 3x-2y=9
View SolutionSolve the following system of equation by Cramer's rule.
x+y+z=9
2x+5y+7z=52
2x+y-z=0
View SolutionFor what values of p and q the system od equations
x+y+z=6
x+2y+3z=10
x+2y+pz=q has
(i) unique sollution ?
(ii) an infinitely many solutions ?
(iii) no solution ?
View SolutionIf the following equations `x+y-3z = 0, (1+lamda)x + (2+lamda) y - 8z = 0, x-(1+lamda)y + (2+lamda)z = 0` are consistent then the value of `lamda` is
View SolutionThe equation `(lambda-1)x+(3lambda+1)y+2lambdaz=0`.
`(lambda-1)x+(4lambda-2)y+(lambda+3)z=0` and `2x+(3lambda+1)y+3(lambda-1)z=0`
gives non-trivial solution for some values of `lambda, then the ratio `x : y : z` when `lambda` has the smallest of these values :
View SolutionGiven x=cy+bz,y=az+cx and z=bx+ay, then prove `a^(2) +b^(2) +c^(2) `+2abc =1.
View SolutionIf `f(x) =|{:(sinx,cosx,sinx),(cosx,-sinx,cosx),(x,1,1):}|` find the value of `2[f'(0)]+[f'(1)]^(2)`
View SolutionLet f(x)=`|{:(cosx,sinx,cosx),(cos2x,sin2x,2cos2x),(cos3x,sin3x,3cos3x):}|` then find the value of `f'((pi)/(2))`.
View SolutionLet `alpha` be a repeated root of a quadratic equation `f(x)=0a n dA(x),B(x),C(x)` be polynomials of degrees 3, 4, and 5, respectively, then show that `|A(x)B(x)C(x)A(alpha)B(alpha)C(alpha)A '(alpha)B '(alpha)C '(alpha)|` is divisible by `f(x)` , where prime `(')` denotes the derivatives.
View SolutionIf `(x)=|(alpha+x,theta+x,lambda+x),(beta+x,varphi+x,mu+x),(gamma+x,psi+x, v+x)|` show that `"Delta^"(x)=0a n d"Delta"(0)+S x ,w h e r eS` denotes he sum of all the cofactors of all elements in `"Delta"(0)a n d` dash denotes the derivative with respect of `xdot`
View Solution`if =|{:(x^(n),,n!,,2),(cos x,,cos.(npi)/(2),,4),(sin x,,sin .(npi)/(2),,8):}|,` then find the value of
`(d^(n))/(dx^(n)) [f(x)]_(x=0) .(n in z).`
View SolutionIf `Delta(x)=|{:(a,b,c),(6,4,3),(x,x^(2),x^(3)):}|` then find `int_(0)^(1) Delta (x)`dx.
View SolutionLet `f(x)=|secxcosx s e c^2x+cotx cos e c\ x cos^2x cos^2x cos e c^2x1cos^2x cos^2x|` . Prove that `int_0^(pi//2)f(x)dx=-pi/4-8/(15)` .
View SolutionLet `"Delta"_r=|r x(n(n+1))/2 2r-1y n^2 3r-2z(n(3n-1))/2|dot` Show that `sum_(r=1)^n"Delta"_r=0`
View SolutionLet n be a positive integer and
`Delta_(r)=|{:(r^(2)+r,r+1,r-2),(2r^(2)+3r-1,3r,3r-3),(r^(2)+2r+3,2r-1,2r-1):}|` and
`sum _(r=1)^(n)Delta_(r)=an^(2)+bn+c` find the value of a+b+c.
View Solutionif `(x_(1)-x_(2))^(2)+(y_(1)-y_(2))^(2)=a^(2), (x_(2)-x_(3))^(2)+(y_(2)-y_(3))^(2)=b^(2) (x_(3)-x_(1))^(2)+(y_(3)-y_(1))^(2)=c^(2).` where a,b,c are positive then prove that `4 |{:(x_(1),,y_(1),,1),(x_(2) ,,y_(2),,1),( x_(3),, y_(3),,1):}| = (a+b+c) (b+c-a)
(c+a-b)(a+b-c)`
View SolutionIf a,b,c are comples number and z=`|{:(,0,-b,-c),(,bar(b),0,-a),(,bar(c),bar(a),0):}|` then show tha z is purely imaginary
View SolutionThe equation `|{:((1+x)^(2),(1-x)^(2),-(2+x^(2))),(2x+1,3x,1-5x),(x+1,2x,2-3x):}|+|{:((1+x)^(2),2x+1,x+1),((1-x)^(2),3x,2x),(1-2x,3x-2,2x-3):}|=0`
View SolutionIf X, Y and Z are positive numbers such that Y and Z have respectively 1 and 0 at their unit's place and `Delta` is the determinant
`|(X,4,1),(Y,0,1),(Z,1,0)|`
If `(Delta + 1)` is divisible by 10, then x has at its unit's place
View SolutionThe number of distinct values of `a2xx2` determinant whose entries are from the set {-1,0,1}, is
View SolutionConsider the polynomial fucntion
`f(x) = |{:((1+x)^(2),,(1+2x)^(b),,1),(1,,(1+x)^(a),,(1+2x)^(b)),((1+2x)^(b),,1,,(1+x)^(a)):}|`
a,b being positive integers.
Which of the following is true ?
View SolutionLet `Delta_(a)=|{:((a-1),n,6),((a-1)^(2), 2n^(2),4n-2),((a-1)^(3),3n^(3),3n^(2)-3n):}|` the value of `sum_(a=1)^(n)Delta_(a)` is
View SolutionIf `Delta (x)=|{:(1,cos x,1-cos x),(1+sin x,cos x,1+sinx-cosx),(sinx,sinx,1):}|` then `int_(0)^(pi//2)Delta(x)` dx is equal to
View SolutionNumber of values of a for which the system of equations `ax+(2-a)y=4+a^(2)` and ax +(2a-1)y=`a^(5)`-2 possess no solution is
View SolutionThe value of determinant `|{:(a^(2),a^(2)-(b-c)^(2),bc),(b^(2),b^(2)-(c-a)^(2),ca),(c^(2),c^(2)-(a-b)^(2),ab):}|` is
View SolutionThe value of `theta` lying between `-(pi)/(4) "and " (pi)/(2)` and `0leAle(pi)/(2)` and satisfying the equation
`|{:(1+sin^(2)A,cos^(2)A,2sin4theta),(sin^(2)A,1+cos^(2)A,2sin4theta),(sin^(2)A,cos^(2)A,1+2sin4theta):}|` =0 are
View SolutionThe digits A,B,C are such that the three digit numbers A88, 6B8, 86 C are divisible by 72 the determinant
`|{:(A,6,8),(8,B,6),(8,8,C):}|` is divisible by
View SolutionIf p,q,r and s are in AP and f(x) =`|{:(p+sinx,q+sinx,q-r+sinx),(q+sinx,r+sinx,-1+sinx),(r+sinx,s+sinx,s-q+sinx):}|` such that
`int_(0)^(1)`f(x) dx =-2, the common difference of the AP can be
View SolutionFind the value of `a \ a n d \ b` if the system of equation `a^2x-b y=a^2-b \ a n d \ b x-b^2y=2+4b` (i) posses unique solution (ii) infinite solutions
View SolutionIf `Delta_(r)=|{:(r,r-1),(r-1,r):}|` where is a natural number, the value of `root(10)(sum_(r=1)^(1024))Delta_(r)` is
View SolutionIf P,Q and R are the angles of a triangle the value of `|{:(tanP,1,1),(1,tanQ,1),(1,1,tanR):}|` is
View SolutionExpand `|(2,0), (3x , 6)|`
View SolutionSuppose a, b and c are distinct and x,y and z are connected by the system of eqations `x+ay+a^(2)z=a^(3),x+by+b^(2)z=b^(3) "and" x+cy+c^(2) z=c^(3).`
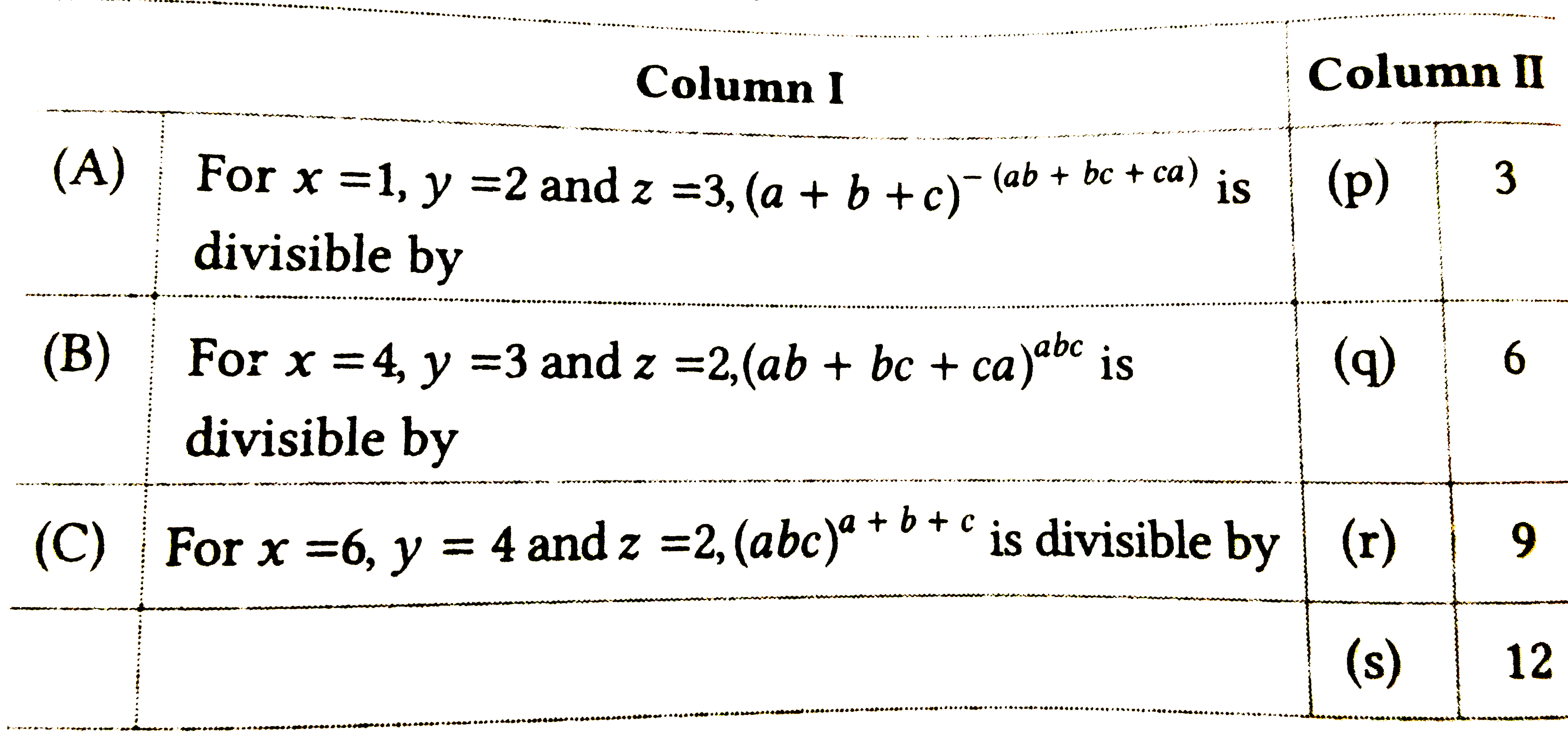
View SolutionConsider the determinant
`f(x)=|{:(0,x^(2)-a,x^(3)-b),(x^(2)+a,0,x^(2)+c),(x^(4)+b,x-c,0):}|`
Statement -1 f(x) =0 has one root x =0.
Statement -2 The value of skew -symmetric determinant of odd order is always zero.
View SolutionA determinant of second order is made with the elements 0 and 1. Find the number of determinants with non-negative values.
View SolutionProve that `|{:(1+a,1,1),(1,1+b,1),(1,1,1+c):}|` =abc `(1+(1)/(a)+(1)/(b)+(1)/(c))`
View Solutionabout to only mathematics
View SolutionProve that: `|-2a a+b a+c b+a-2bb+cc+a c+b-2c|=4(a+b)(b+c)(c+a)`
View Solutionif `bc+ qr= ca+rp = ab+ pq =-1` then prove that
`|{:(ap,,a,,p),(bq,,b,,q),(cr,,c,,r):}|=0`
View SolutionIf `alpha "and" beta` are the roots of the equations
`x^(2)-2x+4=0`,find the value of `|{:(sumalpha,sumalpha^(2),sumalpha^(3)),(sumalpha^(2),sumalpha^(3),sumalpha^(4)),(sumalpha^(3),sumalpha^(4),sumalpha^(5)):}|`.
View SolutionIf `a^2+b^2+c^2=1,` then prove that `|[a^2 +(b^2+c^2)cosθ, ab(1−cosθ), ac(1−cosθ)],[ba(1−cosθ),b^2(c^2+a^2)cosθ,bc(1−cosθ)],[ca(1−cosθ),cb(1−cosθ),c^2+(a^2+b^2)cosθ]|` independent of a,b,c?
View SolutionIf a `ne`0 and a`ne`1, show that
`|{:(x+1,x,x),(x,x+a,x),(x,x,x+a^(2)):}|=a^(3)[1+x((a^(3)-1))/(a^(2)(a-1))].`
View SolutionIf a `ne`0 and a`ne`1, show that
`|{:(x+1,x,x),(x,x+a,x),(x,x,x+a^(2)):}|=a^(3)[1+x((a^(3)-1))/(a^(2)(a-1))].`
View SolutionIf `alpha,beta` are the roots of the equation `ax^2+bx+c=0` and `S_n=alpha^n+beta^n` then evaluate `|[3, 1+s_1, +s_2] , [1+s_1, 1+s_2, 1+s_3] , [1+s_2, 1+s_3, 1+s_4]|`
View SolutionWithout expanding at any stage, evaluate the value of the determinant
`|{:(2,tanAcot B+cotAtanB,tanAcotC+cotAtanC),(tanBcotA+cotBtanA,2,tanBcotC+cotBtanC),(tanCcotA+cotCtanA,tanBcotC+cotBtanC,2):}|.`
View Solutionabout to only mathematics
View SolutionIf `Delta=|{:(sinx,sin(x+h),sin(x+2h)),(sin(x+2h),sinx,sin(x+h)),(sin(x+h),sin(x+2h),sinx):}|`
find `lim_(hto0)((Delta)/(h^(2)))`.
View SolutionIf `f(x)=|(x+c_1,x+a,x+a),(x+b,x+c_2,x+a),(x+b,x+b,x+c_3)|` then show that f(x) is linear in x. Hence deduce`f(0)= (bg(a)-ag(b))/((b-a))` where `g(x)=(c_1-x)(c_2-x)(c_3-x)`
View SolutionIf f(a,b)`=(f(b)-f(a))/(b-a)` and
`f(a,b,c)=(f(b,c)-f(a,b))/(c-a)` prove that `f(a,b,c)=|{:(f(a),f(b),f(c)),(1,1,1),(a,b,c):}|-:|{:(1,1,1),(a,b,c),(a^(2),b^(2),c^(2)):}|`.
View Solutionthe value of the determinant
`|{:((a_(1)-b_(1))^(2),,(a_(1)-b_(2))^(2),,(a_(1)-b_(3))^(2),,(a_(1)-b_(4))^(2)),((a_(2)-b_(1))^(2),,(a_(2)-b_(2))^(2) ,,(a_(2)-b_(3))^(2),,(a_(3)-b_(4))^(2)),((a_(3)-b_(1))^(2),,(a_(3)-b_(2))^(2),,(a_(3)-b_(3))^(2),,(a_(3)-b_(4))^(2)),((a_(4)-b_(1))^(2),,(a_(4)-b_(2))^(2),,(a_(4)-b_(3))^(2),,(a_(4)-b_(4))^(2)):}|` is
View Solution
Examples questions and complete solutions for chapter DETERMINANTS of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS DETERMINANTS
- Determinants Exercise 5:
- Determinants Exercise 7:
- Examples
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 4
- Expansion of Determinant
- Single Option Correct Type Questions