Complete Solutions to Exercise (Single Option Correct Type Questions) of chapter THE STRAIGHT LINES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | THE STRAIGHT LINES |
| ARIHANT MATHS | Exercise (Single Option Correct Type Questions) |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
The straight line `y = x - 2` rotates about a point where it cuts x-axis and become perpendicular on the straight line `ax + by + c = 0` then its equation is
View SolutionIf `2/(1 !9!)+2/(3!7!)+1/(5!5!)=2/(a!),` then orthocentre of the triangle having sides `x-y+1=0,x+y+3=0and 2x+5y-2=0` is
View SolutionIf `f(x+y) = f(x).f(y)` for all `x and y. f(1)=2`, then area enclosed by `3|x|+2|y|le 8` is (A) `f(5)` sq. units (B) `f(6)` sq. units (C) `1/3 f(6)` sq. units (D) `f(4)` sq. units
View SolutionThe graph of the function, `cos x cos (x +2) -cos^2 (x+1)` is
View SolutionA straight line passing through the point`(2,2)` and the axes enclose an area `lamda`. The intercepts on the axes made by the line are given by the two roots of:
(A) `x^2-2|lamda|x+|lamda|=0` (B) `x^2+|lamda|x+2|lamda|=0`
(C) `x^2-|lamda|x+|2lamda|=0` (D) None of these
View SolutionThe set of values of b for which the origin and the point (1, 1) lie on the same side of the straight line, `a^2 x + a by + 1= 0 AA ainR, bgt 0` are(A) `b in (2,4)` (B)` b in(0, 2)` (C) `b in [0, 2]`(D) `(2, oo)`
View SolutionLine `L` has intercepts `a` and `b` on the coordinate axes. When, the axes area rotated through a given angle, keeping the origin fixed, the same line `L` has intercepts `p` and `q`, then
View SolutionIf the distance of any point `(x,y)` from origin is defined as `d(x,y)=max{|x|,|y|}`, then the locus of the point `(x,y)` where `d(x,y)=1` is
View SolutionIf `p_(1),p_(2),p_(3)` be the length of perpendiculars from the points `(m^(2),2m),(mm',m+m')` and `(m^('2),2m')` respectively on the line `xcosalpha+ysinalpha+(sin^(2)alpha)/(cosalpha)=0` then `p_(1),p_(2),p_(3)` are in:
View Solution`A B C D` is a square whose vertices are `A(0,0),B(2,0),C(2,2),` and `D(0,2)` . The square is rotated in the `X Y-p l a n e` through an angle `30^0` in the anticlockwise sense about an axis passing though `A` perpendicular to the `X Y-p l a n e` . Find the equation of the diagonal `B D` of this rotated square.
View SolutionThe point (4,1) undergoes the following three successive transformations ,
reflection about the line `y = x-1`
translation through a distance 1 unit along the positive direction
rotation thrpough an angle `pi/4` about the origin in the anti - clockwise direction
Then the coordinates of the final point are ,
View SolutionIf the square ABCD, where `A(0,0),B(2,0)C(2,2) and D(0,2)` undergoes the following three transformations successively
(i) `f_(1)(x,y) to (y,x)`
(ii) `f_(2)(x,y) to (x+3y,y)`
(iii) `f_(3) (x,y) to ((x-y)/2,(x+y)/2)`
then the final figure is a
View SolutionThe line `x+y=a` meets the axes of x and y at A and B respectively. A triangle AMN is inscribed in the triangle `OAB`, O being the origin, with right angle at N, M and N lie respectively on OB and AB. If the area of the triangle AMN is `3/8` of the area of the triangle `OAB`, then `(AN)/(BM)` is equal to:
View SolutionIf P(1,0), Q(-1,0) and R (2,0) are three given points, then the locus of the point `S` satisfying the relation `(SQ)^2+(SR)^2=2(SP)^2`
View SolutionIf `A((sin alpha)/3 - 1,(cos alpha)/2 - 1)` and B(1,1) `alpha in [ -pi,pi]` are two points on the same side of the line `3x - 2y +1 = 0 ` then `alpha ` belongs to the interval
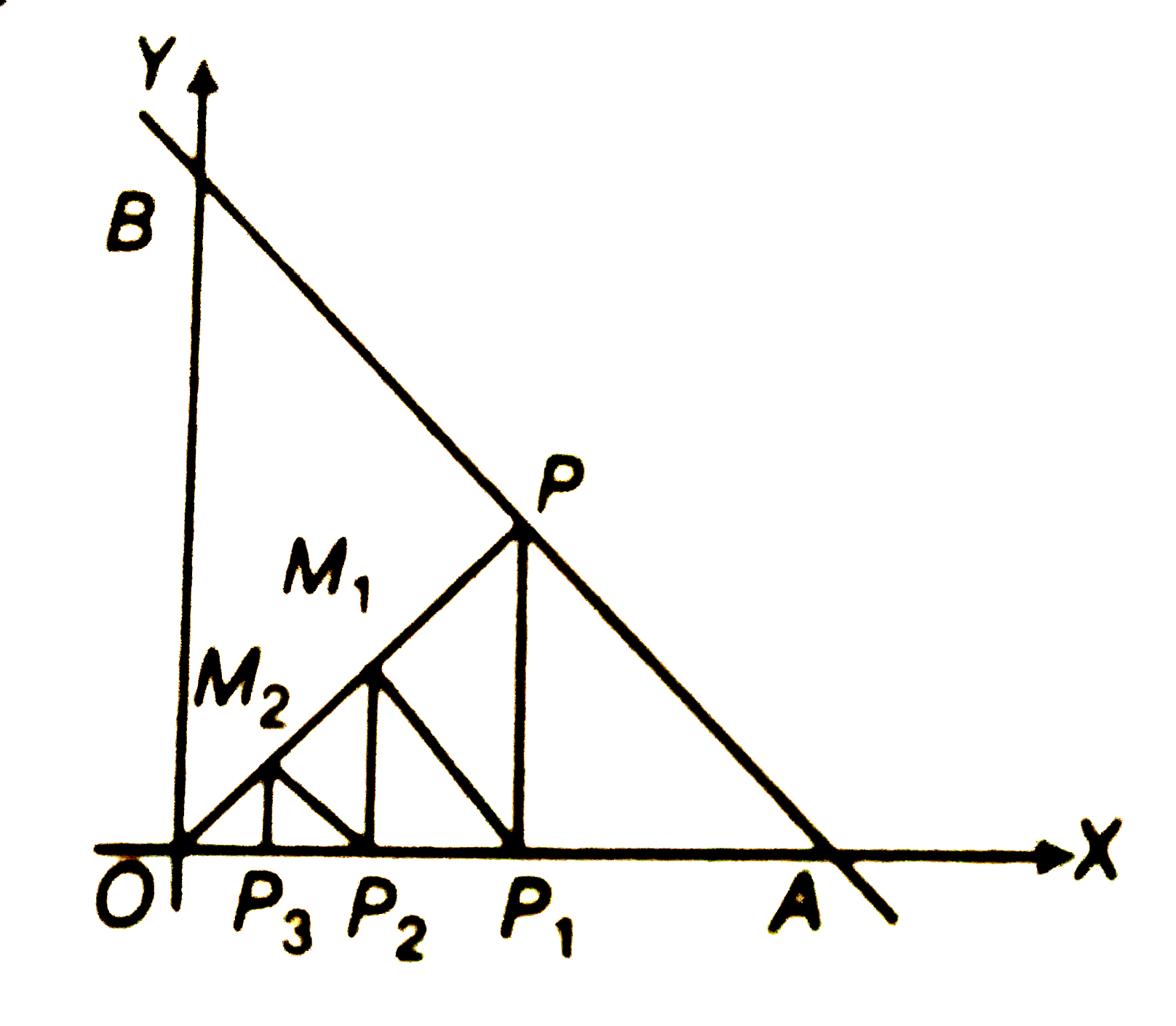
View SolutionThe line `x+y=1` meets X-axis at A and Y-axis at B,P is the mid-point of `AB,P_(1)` is the foot of perpendicular from P to `OA, M_(1)` is that of `P_(1)` from `OP,P_(2)` is that of `M_(1)` from `OA,M_(2)` is that of `P_(2)` from `OP,P_(3)` is that of `M_(2)` from OA and so on. If `P_(n)` denotes theb nth foot of the perpendicular on OA, then find `OP_(n)`
 .
.
View SolutionThe line x = c cuts the triangle with corners (0,0) , (1,1) and (9,1) into two regions .For the area of the two regions to the same , then c must be equal to
View SolutionIf the straight lines `x+2y=9,3x-5y=5` and `ax+by=1` are concurrent , then the straight line `5x+2y=1` passes through the point
View SolutionIf the ends of the base of an isosceles triangle are at (2, 0) and (0, 1), and the equation of one side is `x = 2`, then the orthocenter of the triangle is
View SolutionLet `m ,n` are integers with `0
View SolutionA straight line l with negative slope passes through (8,2) and cuts the coordinate axes at P and Q. Find absolute minimum value of ''OP+OQ`` where O is the origin-
View SolutionDrawn from origin are two mutually perpendicular lines forming an isosceles triangle together with the straight line `2x+y=a` then the area of this triangle is
View SolutionThe number of integral values of `m` for which the x-coordinate of the point of intersection of the lines `3x+4y=9` and `y=m x+1` is also an integer is 2 (b) 0 (c) 4 (d) 1
View SolutionA ray of light coming fromthe point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5,3). The coordinates of the point A is :
View SolutionConsider the family of lines ` 5x+3y-2 + lambda (3x-y-4)=0` and `x-y+1 + mu (2x - y - 2) = 0 ` Equation of straight line that belong to both families is `ax+by-7=0` then `a+b` is
View SolutionIn `Delta ABC` equation of the right bisectors of the sides Ab and AC are `x+y = 0 and x - y = 0 ` respectively .If A = (5,7) then equation of side BC is
View SolutionTwo particles start from point (2, -1), one moving two units along the line x+ y = 1 and the other 5 units along the line x - 2y = 4, If the particle move towards increasing y, then their new positions are:
View SolutionLet P be (5,3) and a point R on y = x and Q on the X - axis be such that `PQ +QR+RP` is minimum ,then the coordinates of Q are
View Solution
Exercise (Single Option Correct Type Questions) questions and complete solutions for chapter THE STRAIGHT LINES of ARIHANT MATHS (HINGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS THE STRAIGHT LINES
- Examples
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 4
- Exercise For Session 5
- Exercise For Session 6