Complete Solutions to वस्तुनिष्ठ प्रश्न of chapter त्रिभुज of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | त्रिभुज |
| ARIHANT PUBLICATION MP | वस्तुनिष्ठ प्रश्न |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
किसी त्रिभुज की तीनों भुजाओं से बराबर दुरी पर रहने वाले बिंदु का बिन्दुपथ होगा।
View Solution`Delta ABC` की भुजाओं BC, CA तथा AB को क्रम से आगे बढ़ाने पर बहिष्कोण `angle ACD, angle BAE` और `angle CBF` बनते हैं, तब `angle ACD + angle BAE + angle CBF` बराबर है
View Solutionयदि `Delta ABC` में, `angle A lt 90^(@)`, तो निम्न में से कौन-सा कथन सत्य होगा ?
View Solution`Delta ABC` की माध्यिकाएँ BE तथा CF एक-दूसरे को G पर काटती है, जब
View Solutionयदि किसी त्रिभुज में एक भुजा का वर्ग शेष दो भुजाओं के वर्गों के योग से अधिक है, तो उन भुजाओं के बीच का कौन होगा
View Solutionएक `Delta ABC` में, `/_ACB = 64^@` है। AB के बिन्दु Q पर लंबवत अर्द्धक BC को P पर मिलता है `/_PAC = 48^@` है, तो `/_ABC` है
View Solutionएक त्रिभुज के अधिककोण तथा एक न्यूनकोण में `20^@` का अन्तर है त्रिभुज के दोनों न्यूनकोण में `56^@` का अन्तर है । दोनों न्यूनकोणों में से एक न्यूनकोण है
View Solution`Delta ABC` में, `angle B` एवं `angle C` के अन्तः अर्द्धक बिंदु O पर मिलते हैं। यदि `angle A = 70^(@)` है, तो `angle BOC` होगा
View Solution`AC` तथा `BD` का कटान बिंदु `O` है | `O` के अतिरिक्त `P` एक अन्य बिंदु है जो कि उसी तल में है जिस तल में `A`, `B`, `C` तथा `D` है | `PA + PB + PC + PD` का मान है
View Solutionकिसी त्रिभुज की भुजाएँ 6, 12 तथा 13 सेमी है। वह त्रिभुज है
View Solutionएक `Delta PQR` में, यदि PQ = 10 सेमी, QR = 20 सेमी, RP = 25 सेमी हो, तो
View Solutionएक समबाहु `DeltaABC` में बिन्दु D, भुजा BC में इस प्रकार है की `BD = (1//5) BC` में `AD^2` और `AB^2` में अनुपात है
View SolutionABC एक समद्विबाहु त्रिभुज हैं, जिसमे AB = AC हैं, भुजा AB पर एक बिंदु L व AC पर एक बिंदु M इस प्रकार हैं कि BC , CL, LM तथा AM बराबर हैं, तो कोण A तथा B अनुपात होगा
View Solution`Delta ABC` में, `angle ABC` तथा `angle ACB` के अर्द्धक O पर मिलते हैं, तो `angle BOC` बराबर हैं
View Solution`Delta ABC` के कोणों B तथा C के आंतरिक द्विभाजक X पर मिलते हैं। यदि `angle A = 60`, तो `angle BXC` हैं
View Solutionसमबाहु `Delta ABC` में, CD भुजा AB की माध्यिका हैं, तो `CD^(2)` बराबर हैं
View Solutionयदि चतुर्भुज ABCD में `angle B = angle D = 90^(@)`, तो `CD^(2) - CB^(2)` का मान बराबर होगा
View SolutionABC एक समकोण त्रिभुज हैं। शीर्ष A से कर्ण BC पर AD लम्ब डाला गया। यदि AB = 5 सेमी तथा AC = 12 सेमी, तो AD की लम्बाई हैं
View Solutionयदि त्रिभुज ABC में, `AB^(2) = BC^(2) + AC^(2) + BC. AC`, तो `angle C` का मान होगा
View Solutionयदि त्रिभुज ABC में, `AB^(2) = BC^(2) + AC^(2) + BC . AC`, तो `angle C` का मान होगा
View Solutionएक समांतर चतुर्भुज की संलग्न भुजाएँ 16 तथा 18 सेमी लम्बी हैं। एक विकर्ण 26 सेमी है, तो दूसरे विकर्ण की लम्बाई होगी
View Solutionयदि किसी त्रिभुज की दो भुजाएँ 16 तथा 18 सेमी है तथा तीसरी भुजा की माध्यिका 11 सेमी है, तो तीसरी भुजा की लम्बाई होगी
View Solutionएक समकोण समद्विबाहु त्रिभुज की भुजा 8 सेमी है। भुजा का कर्ण पर प्रक्षेप होगा
View SolutionABC एक त्रिभुज है। इसकी माध्यिकाएँ बिन्दु O पर काटती है। `(AB^(2)+BC^(2)+AC^(2))` बराबर है
View Solutionसमबाहु त्रिभुज ABC के बाहर रेखा BC पर कोई बिंदु D हैं, तो `AD^(2)` बराबर हैं
View Solutionएक समद्विबाहु त्रिभुज `ABC` में, यदि `AC = BC` तथा `AD, BC` पर लम्ब हैं, तो `AB^(2)` का मान बराबर होगा
View Solutionकिसी भी समकोण त्रिभुज में कर्ण की माध्यिका कर्ण की होती हैं
View SolutionABCDEF एक समषटभुज हैं जिसकी प्रत्येक भुजा a हैं। इस समषटभुज के विकर्ण AC की लम्बाई होगी
View Solutionएक समकोण `Delta ABC, B` पर इस प्रकार समकोणिक हैं कि AB = 12 सेमी तथा BC = 16 सेमी। बिंदु B से कर्ण AC पर लम्ब बनाया जाता हैं जोकि D पर मिलता हैं। लम्ब BD की लगभग लम्बाई हैं
View Solutionएक समकोणीय त्रिभुज ABC, B पर समकोणिक हैं। बिंदु A से दो रेखाएँ खींची गई हैं जो रेखा BC को क्रमशः D तथा E पर मिलती हैं। बिंदु D तथा बिंदु E रेखा BC को तीन समान भागों में विभक्त करते हैं, तो
View Solutionत्रिभुज ABC में, लम्ब AD की लम्बाई 10 सेमी हैं। यदि `BD = (10)/(sqrt(3))` सेमी तथा `CD = 10 sqrt(3)` सेमी, तो `angle BAC` बराबर हैं
View Solutionत्रिभुज ABC में, `angle B = 70^(@), angle C = 40^(@)` | BC पर बिंदु P तथा Q इस प्रकार हैं कि AP, `angle BAC` का आंतरिक अर्द्धक हैं `AQ bot BC` तथा हैं। ऐसी स्थिति में `angle QAP` बराबर हैं
View Solutionसमान्तर चतुर्भुज का क्षेत्रफल होता है :
View Solutionदो ऊर्ध्वाधर खम्बे A तथा B जोकि क्रमशः 4 तथा 6 मी ऊँचे हैं, समतल सतह पर खड़े है। दोनों के बीच की दूरी 5 मी हैं। एक तार खम्भे A तथा B को जमीन से क्रमशः 3 तथा 4 मी की ऊँचाइयों पर जोड़ती है। एक अन्य तार इन्हीं खम्भों को क्रम से 4 तथा 5.5 मी ऊँचाइयों पर जोड़ता है। दोनों तारों की लम्बाइयों में लगभग अंतर होगा
View Solutionएक समकोण त्रिभुज ABC में कोण B समकोण है | यदि भुजाओ AB और BC पर क्रमश: बिंदु P और Q है, तो
View Solutionएक समकोणिक त्रिभुज ABC, B पर समकोण बनाता है। A से खींची गई रेखा BC को E पर तथा C से खींची गई रेखा AB को D पर इस प्रकार मिलती है कि AE = CD = 13 सेमी, BE = 5 सेमी तथा AD = CE, तब AD कि लम्बाई होगी
View Solutionचित्र में, रेखा `DE || BC` यदि AB : DB = 3:1 और रेखाखण्ड EA = 3.3 सेमी हो, तो रेखाखण्ड EC की माप होगी

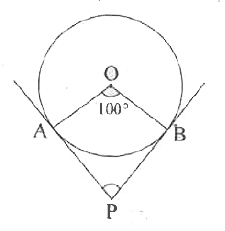
View Solutionदिये गये चित्र में , OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण `100^(@)` का है। यदि बहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो ,तो `angleAPB` का मान है -
View Solutionत्रिभुज `ABC` का आधार `10` सेमी है। एक रेखा `XY` जिसकी लम्बाई `3` सेमी है, आधार `BC` के समांतर खींची गई है, जो भुजा को `AB` व `AC` क्रमशः `X` तथा `Y` पर काटती है। यदि `AC = 5` सेमी हो, तो `AY` का मान होगा
View Solutionएक त्रिभुज ABC में, एक रेखा DE भुजा BC के समांतर खींची गई है जोकि AB को D पर तथा AC को E पर इस प्रकार मिलती है कि त्रिभुज ADE तथा समलम्ब चतुर्भुज BDEC के क्षेत्रफल 1:2 के अनुपात में हैं। भुजा DE : BC का अनुपात है
View Solutionएक `Delta ABC` में, बिन्दु D रेखा AB पर तथा बिन्दु E रेखा AC पर इस प्रकार है कि DE, BC के समान्तर है। यदि `AD=2x-3, BD=x-1, AE=5x-7` तथा `EC=2(x-1)`, तो x का मान है
View Solutionदो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 25 वर्ग सेमी तथा 36 वर्ग सेमी हैं, तो उनकी संगत भुजाओं में अनुपात होगा
View Solutionदो समरूप त्रिभुजों की ऊँचाइयाँ क्रमशः 2 सेमी तथा 3 सेमी है। उनके क्षेत्रफलों में अनुपात होगा
View Solutionयदि `Delta ABC, angle A` पर समकोण है तथा AN, BC रेखा पर लम्ब है, जबकि BC = 12 सेमी तथा AC = 6 सेमी, तब `(Delta ANC" का क्षेत्रफल")/(Delta ABC" का क्षेत्रफल")` होगा
View Solution`Delta ABC` में `angle A` की अन्तः तथा बाह्य अर्द्धक रेखाएँ आधार BC को क्रमशः D और E बिन्दु पर काटती है, यदि BC = 7 सेमी, CA = 4 सेमी और AB = 6 सेमी, तो DE की माप होगी
View Solution`Delta ABC`, में AB = 4 सेमी, BC = 5 सेमी तथा AC = 3 सेमी। एक अन्य त्रिभुज DEF = 8 सेमी, EF = 10 सेमी तथा FD = 6 सेमी। शीर्ष A से BC पर लम्ब AP तथा शीर्ष D से EF पर DM लम्ब खींचे गए हैं। AP तथा DM की लम्बाइयों में अनुपात होगा
View Solutionएक त्रिभुज PQR इस प्रकार है, कि PR = 6 सेमी, P से 3 सेमी की दुरी पर PQ भुजा पर एक बिन्दु S है। SR को मिलाने से बना कोण `angle PRS, angle PQR` के बराबर है। PQ की लम्बाई होगी
View Solutionएक त्रिभुज ABC में, बिंदु P भुजा AB को दो भागो में तथा बिंदु Q भुजा AC को दो भागो में इस प्रकार काटते हैं। कि PQ || BC है। PQ त्रिभुज ABC को दो भागो में बाँटती है जोकि क्षेत्रफल में समान है। BP : AB होगा
View Solutionदो समरूप त्रिभुजों के क्षेत्रफल छोटे त्रिभुज के क्षेत्रफल का 36 गुना है। बड़े त्रिभुज की एक भुजा और छोटे त्रिभुज की संगत भुजा की लम्बाई में अनुपात होगा
View Solutionएक त्रिभुज ABC के अंदर कोई बिंदु O है तथा `angleAOB, angleBOC` तथा `angle COA` के समद्विभाजित रेखा AB, BC तथा CA पर क्रमशः बिंदु D, E तथा F पर मिलते हैं, तब `AD xx BE xx CF` बराबर होगा
View Solution`Delta ABC` इस प्रकार हैं, कि AB = 3 सेमी, BC = 2 सेमी और AC = 2.5 सेमी। `Delta DEF, Delta ABC` के समरूप है, यदि EF = 4 सेमी तब `Delta DEF` का परिमाप है
View Solution
वस्तुनिष्ठ प्रश्न questions and complete solutions for chapter त्रिभुज of ARIHANT PUBLICATION MP of Class 12