Complete Solutions to अभ्यास प्रश्नमाला of chapter केन्द्रीय प्रवृत्ति की मापें of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | केन्द्रीय प्रवृत्ति की मापें |
| ARIHANT PUBLICATION UP | अभ्यास प्रश्नमाला |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
4, 9, 11, x और 14 का समान्तर माध्य 10 है, तो x का मान है
View Solutionप्रथम दस प्राकृत संख्याओं की माधियका ज्ञात करे।
View Solutionप्रथम दस अभाज्य संख्याओं की माध्यिका है
View Solution100 पदों का माध्य 49 है। बाद में यह पाया गया कि तीन पद जोकि 60, 70, 80 होने चाहिए, गलती से क्रमश: 40, 20, 50 पढ़े गए थे। सही माध्य है
View Solutionसंख्याओं का, एक समूह तीन बार 4, पाँच बार 5, छ: बार 6, आठ बार 8 तथा सात बार 10 रखता है। तब संख्याओं के समूह का बहुलक है-
View Solutionयदि 5, 3, 0.5, 4.5, x, 8.5, 9.5 की माध्य 7 है, तो x का मान है
View Solution4, 7,x और 9 का समान्तर माध्य 7 है। x का मान होगा
View Solution60 लड़कों का भार निम्न चार्ट के अनुसार है

इसकी माध्यिका है
View Solution17 प्रेक्षणों का माध्य मान 30 है। यदि प्रथम 9 प्रेक्षणों का माध्य मान 35 है तथा अन्तिम 9 प्रेक्षणों का माध्य मान 23 है, तो नौवें प्रेक्षण का मान -
View Solutionआँकड़ों को आरोही या अवरोही क्रम में रखकर ही केन्द्रीय प्रवृत्ति की कौन-सी माप ज्ञात की जाती है?
View Solutionनिम्न ऑकड़ों के लिए माध्य, माध्यिका और बहलक में सम्बन्ध है -3,-2, 0, 2, 3, 5, 5,5,7,8,9,10
View Solutionकिसी कक्षा A में 49 छात्रों की उपस्थिति का समान्तर माध्य 40% है तथा 53 छात्रों की कक्षा B में इनका मान 35% है, तो कक्षा A तथा B का सम्मिलित माध्य होगा
View Solutionकिसी व्यक्ति पर एक इन्जैक्शन की प्रतिक्रिया का समय क्रमशः 0.53, 0.45, 0.50, 0.49,0.52, 0.54,0.42 तथा 0.55 सेकण्ड पाया गया। व्यक्ति पर इन्जैक्शन की प्रतिक्रिया की माध्यिका एवं समान्तर माध्य का अन्तर होगा
View Solution`M` छात्रों की एक कक्षा के प्रति छात्र औसत अंक `N` पाए गए। सत्यापन के पश्चात दो छात्रों के अंकों में त्रुटि पाई गई। त्रुटि निवारण के उपरान्त एक छात्र के `5` अंक बढ़े जबकि दूसरे छात्र के `7` अंक कम हुए। सभी औसत अंक होंगे
View Solutionएक स्कूल के 15 अध्यापकों के भारों का समान्तर माध्य 58 किग्रा अभिलिखित किया गया है। बाद में यह पाया गया कि एक अध्यापक, जिसका वास्तविक भार 87 किग्रा था, 78 किग्रा अभिलिखित कर दिया गया था। वास्तविक समान्तर माध्य था
View Solutionएक कक्षा के 15 बालकों के वजन नीचे दी गई सारणी के अनुसार हैं

बालकों के वजन के बंटन की माध्यिका होगी
View Solutionनिम्नलिखित बंटन की माध्यिका है

View Solutionनिम्न विवरण (डाटा) का माध्य (अर्थमेटिक मीन) होगा
67, 65, 71, 57 एवं 45 .
View Solutionगणित के एक प्रश्न-पत्र में प्राप्त छात्रों के अंकों की बारम्बारता का वितरण नीचे दिया गया है

अंकों की माध्यिका है।
View Solutionतीन संख्याओं 4, 6 और 8 की बारम्बारताएँ क्रमश: (x + 2), x व (x - 1) हैं। यदि बंटन का समान्तर माध्य 5.76 हो, तब x का मान है।
View Solutionआरोही क्रम में रखी संख्याओं 1,3,5,7, 12, (x + 1), (x + 39, 16, 17, (x + 70, 22 और 25 की माध्यिका 14 है, तब x का मान है
View Solutionएक कक्षा के 30 छात्रों की ऊँचाई निम्नवत् है

एक छात्र जिसकी ऊँचाई 144 सेमी है कक्षा में सम्मिलित होने पर ऊँचाई की माध्यिका में परिवर्तन होगा
View Solution10 व्यक्तियों के समूह की मासिक आय का औसत ₹ 1500 है। एक सदस्य, जिसकी मासिक आय ₹ 1350 है, समूह से चला गया एवं एक नया सदस्य, जिसकी मासिक आय ₹ 1200 है, समूह मे सम्मिलित हो गया। नये समूह की मासिक आय है
View Solutionसारणी में दिए गए आँकड़ों का बहुलक बताइए।

View Solutionएक दुकान में निम्नलिखित बंटन के अनुसार एक दिन में 100 जोड़े जूते बिके। इस बंटन (जूते के माप) का बहुलक है

View Solutionमाध्यिका होती है
View Solutionn संख्याओं `x_(1),x_(2),x_(3),...,x_(n),` का औसत M है। यदि 'x_(n)' को बदलकर `x_(1)` कर दिया जाए, तो नया औसत होगा
View Solutionयदि n प्रेक्षणों `x_(1), x_(2), x_(3),......,x_(n)` का समांतर माध्य `bar(x)` है, तो `sum_(i=1)^(n) (x_(i) - bar(x))` बराबर है-
View Solutionएक विद्यार्थी के मासिक परीक्षा मे पाँच विषयों के प्राप्तांक 2, 3, 4, 5, 6 हैं। प्राप्तांक 4 दिए गए अंकों का
View Solutionचार्ट में दिए गए आवृत्ति वितरण का बहुलक है

View Solutionनिम्नलिखित बंटन का माध्य होगा

View Solutionकॉलोनी के 100 निवासियों की माध्य आय निम्नलिखित आँकड़ों से है
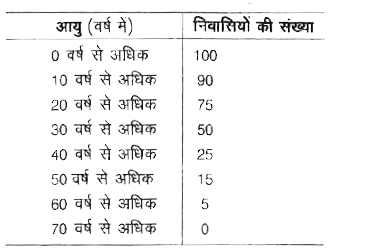
View Solutionएक कक्षा के 5 छात्र क्लास टेस्ट में नीचे दिए गए अंक प्राप्त करते हैं, जहाँ सम्पूर्ण अंक योग 50 है
20, 24, 27, 38, 18, 42, 35, 21, 44, 28, 19, 31, 26, 36, 41 माध्यिका प्राप्तांक है
View Solution20 मापों के माध्य की गणना 56 सेमी की गई। बाद में यह पाया गया कि 64 सेमी का एक माप गलती से 61 सेमी अभिलिखित किया गया। सही माध्य था
View Solutionपाच संख्याओं का माध्य 18 है। यदि एक संख्या हटा दी जाती है, तो माध्य 16 हो जाता है । हटाई गयी संख्या है।
View Solutionनीचे दी गई तालिका के अनुसार मजदूरी एवं मजदूरों का विवरण है

माध्यिका मजदूरी का मान है
View Solutionएक साधारण बंटन का माध्य और माध्यिका क्रमश: 38 और 39 हैं। बहुलक होगा
View Solutionएक मासिक परीक्षा में कक्षा के 16 विद्यार्थियों के गणित में प्राप्तांक हैं 0. 0,2,2,3,3, 3, 4, 5,5,5,5,6, 6, 7.8 प्राप्तांकों का समान्तर माध्य है।
View Solutionनिम्न दो पाई चित्र दो राज्यों में कर्मचारियों के धार्मिक बंटन को दर्शाते हैं। चित्र के आधार पर निम्न प्रश्नों के उत्तर दीजिए।
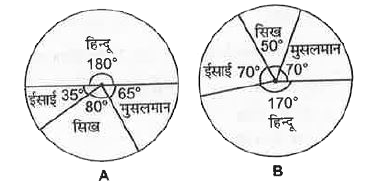
A राज्य में हिन्दुओं की प्रतिशत मात्रा है
View Solutionनिम्न दो पाई चित्र दो राज्यों में कर्मचारियों के धार्मिक बंटन को दर्शाते हैं। चित्र के आधार पर निम्न प्रश्नों के उत्तर दीजिए।
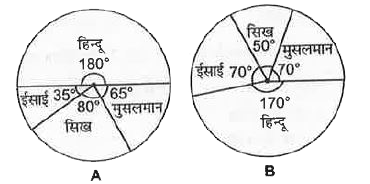
दोनों राज्यों में सिख जनसंख्या का प्रतिशत अन्तर है
View Solutionनिम्न दो पाई चित्र दो राज्यों में कर्मचारियों के धार्मिक बंटन को दर्शाते हैं। चित्र के आधार पर निम्न प्रश्नों के उत्तर दीजिए।
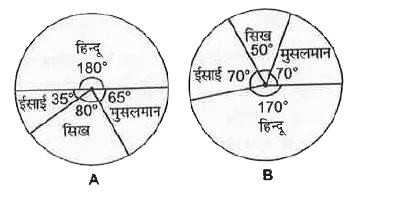
यदि राज्य B की जनसंख्या 540000 है, तब मुस्लिम जनसंख्या है
View Solution(प्र.सं. 42 और 43) निम्नांकित पाई चित्र में एक विद्यार्थी द्वार विभिन्न विषयों में प्राप्त अंकों के त्रिज्यखण्ड कोण प्रदर्शित हैं। यदि के उसके द्वारा प्राप्त कुल अंक 540 हैं, तो पाई चित्र का अध्ययन कर। र निम्न प्रश्नों के उत्तर दीजिए।
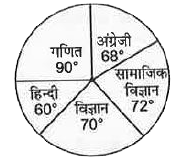
विद्यार्थी द्वारा गणित विषय में प्राप्त अंक हैं
View Solution(प्र.सं. 42 और 43) निम्नांकित पाई चित्र में एक विद्यार्थी द्वार विभिन्न विषयों में प्राप्त अंकों के त्रिज्यखण्ड कोण प्रदर्शित हैं। यदि के उसके द्वारा प्राप्त कुल अंक 540 हैं, तो पाई चित्र का अध्ययन कर। र निम्न प्रश्नों के उत्तर दीजिए।
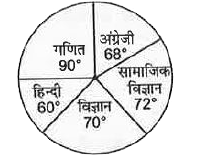
विद्यार्थी द्वारा 108 अंक प्राप्त किए गए हैं
View Solution
अभ्यास प्रश्नमाला questions and complete solutions for chapter केन्द्रीय प्रवृत्ति की मापें of ARIHANT MATHS (HINDI) of Class 12