Complete Solutions to अभ्यास प्रश्न 4.2 of chapter आव्यूह of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | आव्यूह |
| BALAJI PUBLICATION | अभ्यास प्रश्न 4.2 |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
बताओं की क्या निम्न आव्यूह गुणनफल के अनुरूप है अथवा नहीं ?
(i) `A=[(-1,2),(3,4)]," "B=[(5),(6)]`
(ii) `A=[(-5,-7),(6,-8)]," "B=[(3, 4)]`
(iii) `A=[(1,2,3),(4,0,5),(6,7,0)]," "B=[(1,0,2,4),(3,7,0,0)]`
View Solutionआव्यूह B ज्ञात करें यदि `A=[(1,4),(3,2)]` तथा `A+2B=A^(2)`
View Solutionयदि `A=[(2,3,1),(-1,2,3),(2,0,10)]` हो तो `A^(2)` ज्ञात करो।
View Solutionयदि `A=[(0,1),(1,0)]` तथा `B=[(1,0),(0,-1)]` है तो सिद्ध कीजिये-
(i) `A^(2)=B^(2)=I` (ii) `AB=-BA`
View Solutionयदि `A=[(0,0,1),(2,-3,0),(1,1,-1)]` ज्ञात कीजिए `A^(3)+4A^(2)-A`
View Solutionयदि `A=[(2,0,-1),(2,3,-2),(0,-2,5)]` तब `A^(2)+2A-7I` का मान ज्ञात करो।
View Solutionनिम्नलिखित को ज्ञात कीजिए
`[(1,-2,3),(-4,2,5)]xx[(2,3),(4,5),(2,1)]`
View Solutionयदि `theta-phi=pi//2` है तो सिद्ध कीजिए की-
`[(cos^(2) theta,cos theta sin theta),(cos theta.sintheta,sin^(2) theta)][(cos^(2) phi,cos phi sin phi),(cos phi.sin phi,sin^(2) phi)]=0`
View Solutionयदि `A=[(1,3,-1),(2,2,-1),(3,0,-1)]` तथा `B=[(-2,3,-1),(-1,2,-1),(-6,9,-4)]` है तो दिखाइए की `AB=BA`
View Solutionयदि `A=[(1,0),(1,1)], B=[(2,0),(1,1)]` तथा `C=[(-1,2),(3,1)]` है तो दिखाइए की-
(a) `(AB)C=A(BC)`
(b) `A(B+C)=AB+AC`
(c) `(B+C)A=BA+CA`
View Solutionयदि `F(x)=[(cos x,-sin x,0),(sin x,cos x,0),(0,0,1)]` है तो दिखाइए की- `F(x).F(y)=F(x+y)`
View Solutionयदि `[(x,0),(2,x+y)][(1,0),(0,1)]=[(2,1),(1,3)]-2[(0,1//2),(-1//2,3//2)]` हो तो x तथा y के मान ज्ञात कीजिये।
View Solutionयदि `omega`, इकाई के एक घनमूल है तो सिद्ध कीजिए की-
`{[(1,omega,omega^(2)),(omega,omega^(2),1),(omega^(2),1,omega)]+[(omega,omega^(2),1),(omega^(2),1,omega),(omega,omega^(2),1)]}[(1),(omega),(omega^(2))]=[(0),(0),(0)]`
View Solutionएक निर्माता तीन प्रकार की वस्तुएँ A, B, C निर्मित करता है जोकि दिल्ली तथा मुंबई में बेचीं जाती हैं। इन वस्तुओं की वार्षिक बिक्री नीचे दी गयी है। यदि A, B तथा C बस्तुओं का विक्रय मूल्य क्रमशः 2, 3 व 4 रुपये प्रति इकाई है तो आव्यूह का प्रयोग करके प्रत्येक स्थान के लिए कुल प्राप्ति की गणना कीजिए-
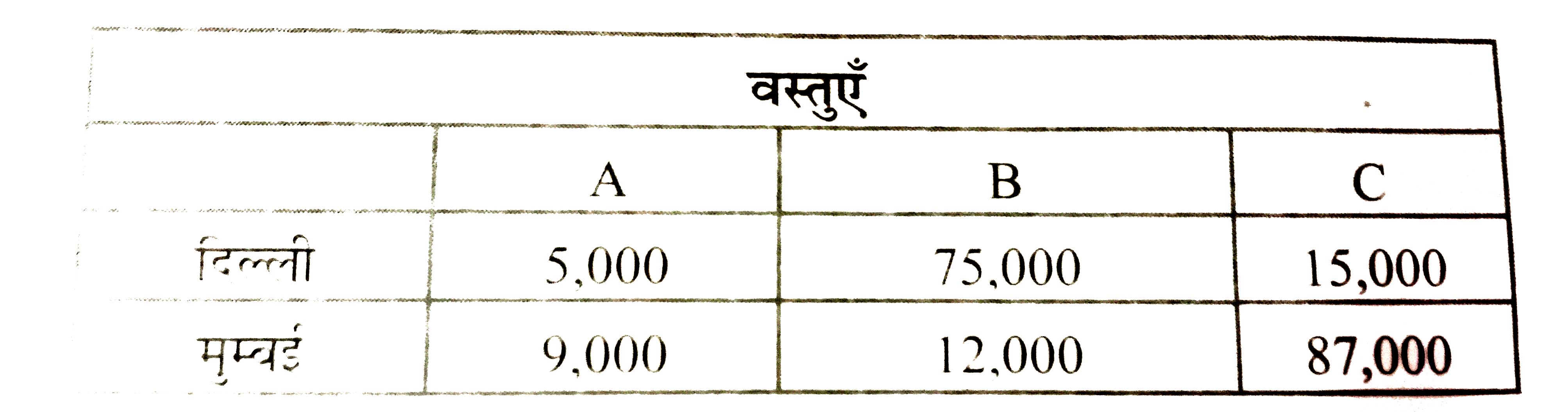
View Solutionयदि `A=[(1,-1),(-1,1)]` तथा `B=[(1,1),(1,1)]` तो सिद्ध कीजिए की AB शून्य आव्यूह है।
View Solutionयदि `A_(alpha)=[(cos alpha,sin alpha),(-sin alpha,cos alpha)]` तो सिद्ध कीजिए की-
(i) `A_(alpha).A_(beta)=A_(alpha+beta)` (ii) `A_(alpha).A_((-alpha))=I`
View Solutionयदि `A=[(1,-1),(-1,1)]` तब सिद्ध कीजिए की `A^(3)=4A`
View Solutionयदि `A=[(3,3,5),(2,3,4),(5,2,3)]` तो सिद्ध कीजिए की `AI_(3)=I_(3)A`
View Solutionयदि `A=[(1,2,5),(3,4,5)], B=[(4,0),(2,1),(1,5)]` तो सिद्ध कीजिए की `AB=[(13,27),(26,34)]`
View Solutionयदि `A=[(2,0,0),(0,2,0),(0,0,2)]` तथा `B=[(x_(1),y_(1),z_(1)),(x_(2),y_(2),z_(2)),(x_(3),y_(3),z_(3))]` तो सिद्ध कीजिए की `AB=2B`
View Solution(i) यदि `A=[(0,i),(i,0)], i^(2)=-1` तब सिद्ध कीजिए की `A^(2)=[(-1,0),(0,-1)]`
(ii) यदि `A=[(0,1),(1,0)]` तो सिद्ध कीजिए की `A^(4)=[(1,0),(0,1)]`
View Solution
अभ्यास प्रश्न 4.2 questions and complete solutions for chapter आव्यूह of SHREE BALAJI MATHS (HINDI) of Class 12