Complete Solutions to अभ्यास प्रश्न 19.1 of chapter सदिश बीजगणित of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सदिश बीजगणित |
| BALAJI PUBLICATION | अभ्यास प्रश्न 19.1 |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
ABCD एक चतुर्भुज है, तो सिद्ध कीजिये की `vec(BA)+vec(BC)+vec(CD)+vec(DA)=2vec(BA)`
View Solutionनिम्न चित्र से सदिश ज्ञात कीजिये।

View Solutionपार्श्व चित्र में त्रिभुज ABC में सदिश `vec(AB)` तथा `vec(BC)` का योगफल ज्ञात कीजिये।
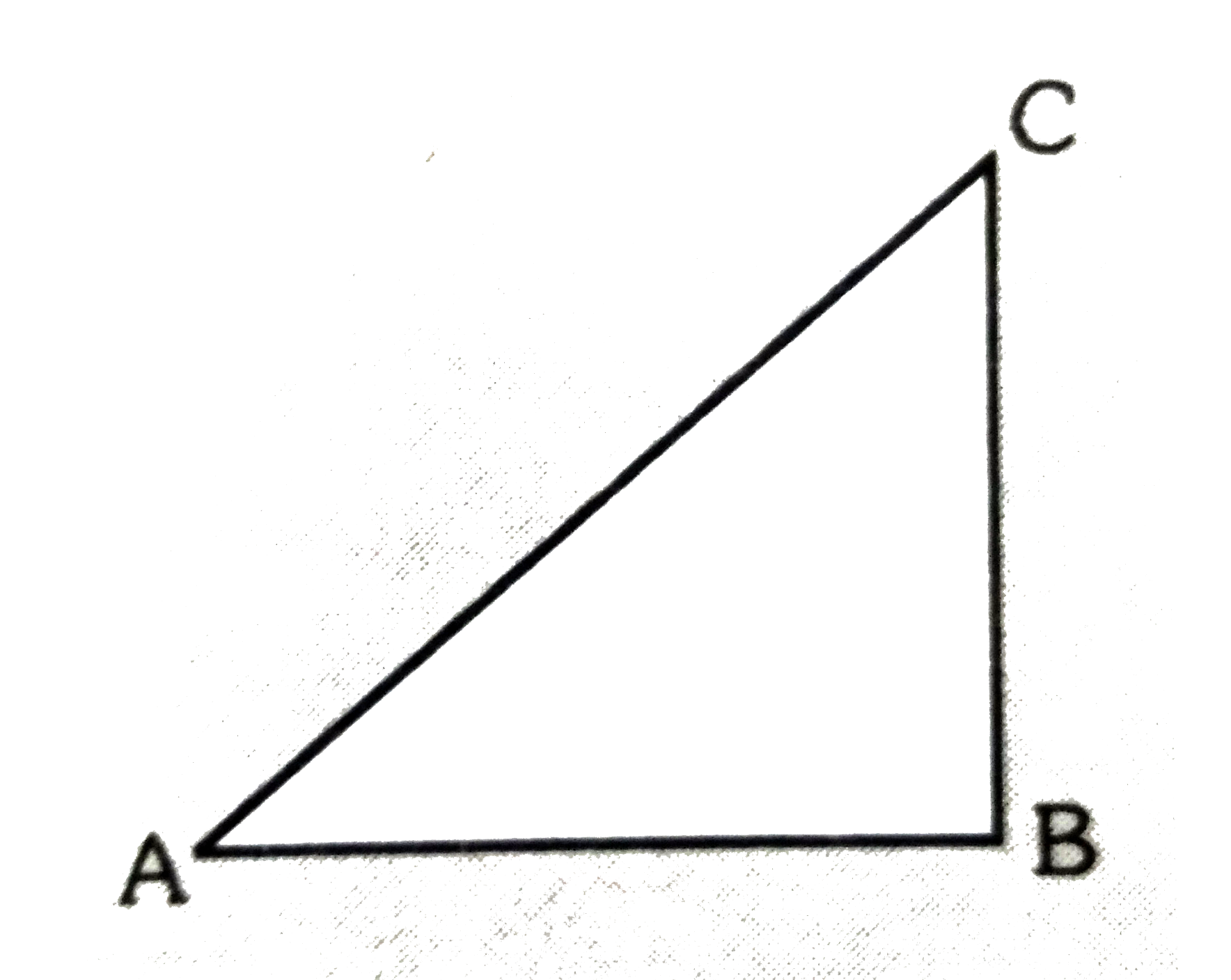
View Solutionयदि `vec(OA)=vec(a), vec(OB)=vec(b)` तो सदिश `vec(BA)` का मान ज्ञात कीजिये।
View SolutionA, B, C, D चार बिन्दुओं के स्थिति-सदिश क्रमशः `veca, vecb, 2veca+3vecb, veca-2vecb` है। `vec(AC), vec(DB), vec(BC)` तथा `vec(CA)` सदिशों को `veca` तथा `vecb` के पदों में प्रकट करो।
View Solutionपार्श्व चित्र में `OA=veca,AB=vecb` तो `vec(OB)` तथा `vec(CD)` ज्ञात करो जबकि C, D क्रमशः OA और AB के मध्य बिन्दु है।
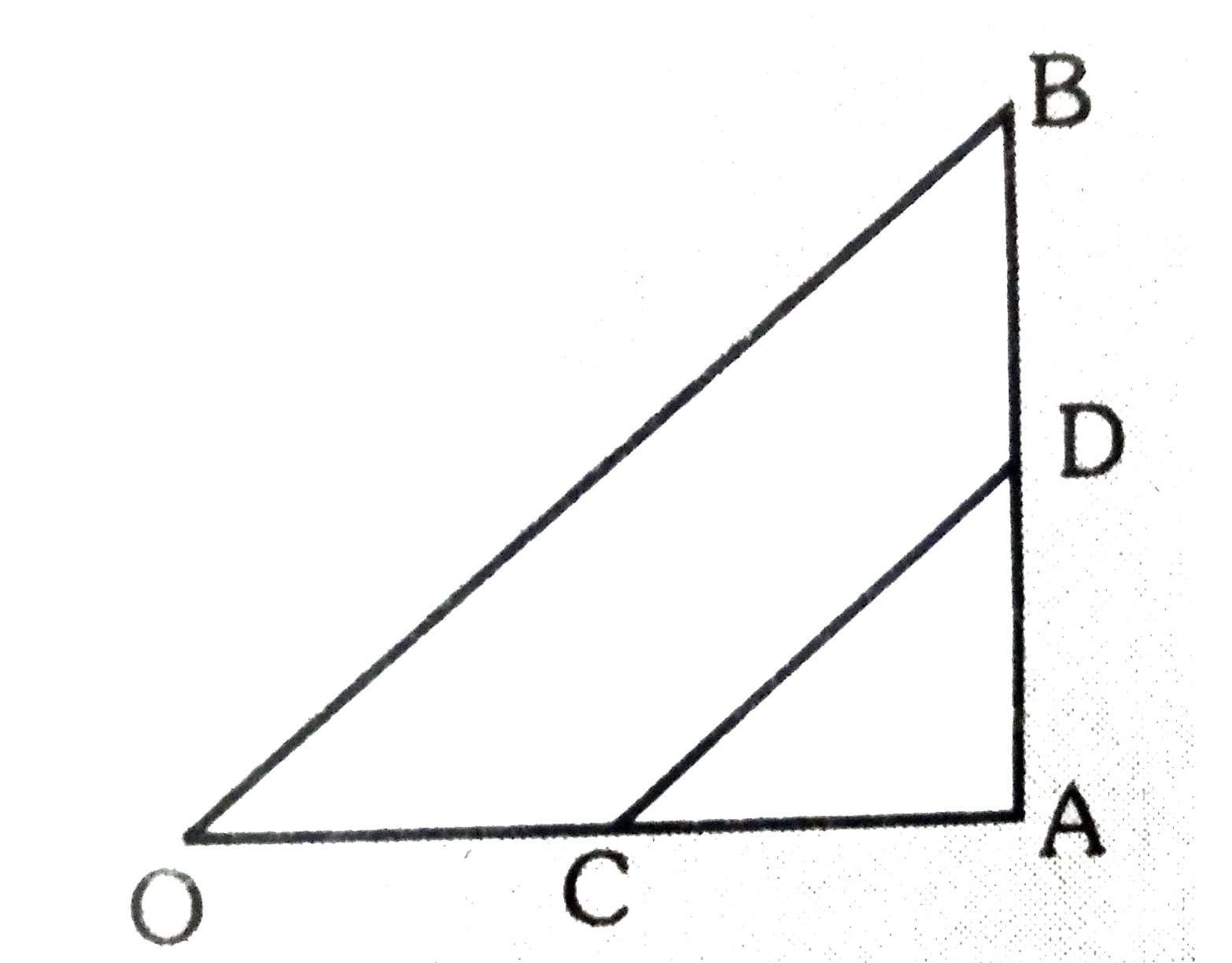
View SolutionABCD एक चतुर्भुज है तथा AC और BD इसके विकर्ण है। सिद्ध करो कि सदिश
`vec(AB)+vec(DC)=vec(AC)+vec(DB)`
View Solutionयदि एक समषटभुज की दो आसन्न भुजाओं से निरूपित सदिश a तथा b हो, तो क्रमशः अन्य भुजाओं से निरूपित सदिश क्या होंगे?
View Solutionत्रिभुज ABC का केन्द्रक G है, तो सिद्ध कीजिये कि
`vec(GA)+vec(GB)+vec(GC)=0`
View SolutionABCD एक समान्तर चतुर्भुज के विकर्ण P पर मिलते है, O कोई बिन्दु है। सिद्ध करो कि सदिश `vec(OA)+vec(OB)+vec(OC)+vec(OD)=4vec(OP)`
View SolutionD, E, F त्रिभुज ABC की भुजाओं के मध्य बिन्दु है दिखाइये कि किसी बिन्दु O के लिए सदिश
`vec(OA)+vec(OB)+vec(OC)=vec(OD)+vec(OE)+vec(OF)`
View SolutionABCDE एक पंचभुज है। बल AB, AE, BC, DC, ED तथा AC एक बिन्दु पर क्रिया करते है। सिद्ध करो कि इनका परिणामी बल `3vec(AC)` है।
View Solution
अभ्यास प्रश्न 19.1 questions and complete solutions for chapter सदिश बीजगणित of SHREE BALAJI MATHS (HINDI) of Class 12