Complete Solutions to Exercise 1 of chapter THERMODYNAMICS of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | THERMODYNAMICS |
| BANSAL | Exercise 1 |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
Out of boiling pont (I), entropy (II), pH (III) and density (IV), Intensive properties are :
View SolutionConsider the reaction at 300 K
`H_(2)(g)+Cl_(2)(g) to 2HCl(g)" "DeltaH = - 185 kJ//mol`
Calculate `DeltaU` if 3 mole of `H_(2)` completely react with 3 mo,le f of `Cl_(2)` to from HCl.
View SolutionEthyl choride `(C_(2)H_(4)(g)Cl)`, is prepared byt reaction of ethylen with hydrogen chloride :
`C_(2)H_(4)(g) + HCl to C_(2)H_(5)Cl(g)`
What is the value of `DeltaU` (in kJ), if 70 g ethlene and 73 g of HCl are allowed to react at 300 K.
View SolutionWhat is `DeltaU` for the process described by figure . Heat supplied during the process `q= 100 kJ`

View SolutionWhat is the change in internal energy when a gas constants from 377 ml to 177 ml under a constant
pressure of 1520 torr , while at the same time being cooled by removing 124 J heat ?
[Take :(1 L atm )n= 100 J]
View SolutionThe heat capcity of liquild water is `75.6 J //mol .K`, while the enthalpy of fusion of ice is `6.0 kJ//mol`, What
is the smallest number of ice cubes at ` 0^(@)` C, each containig ` 9.0g` of water ,needed to cool 500 g of liquild
water from j `20^(@)` to `0^(@)` C ?
View SolutionAn ideal gas is taken around the cycle ABCD A as shown in figure . The net work done during the cycle
is equal to :

View SolutionMolar heat capacity of water in equilibrium with ice at canstant pressure is
View SolutionA cyclic process ABCD is show in PV diagram for a ideal gas . Which of the
following digram reppresents the same process ?

View SolutionOne mole of an ideal monoatomic gas expanded irreversibly in two stage expansion .
`"State"-1" "("8.0 bar, 4.0 liters, 300K")`
`"State"-2" "("2.0 bar, 16 liters, 300K")`
`"State"-3" "("1.0 bar, 32 liters, 300K")`
Total heat absored by the gas in the process is :
View SolutionWhat is the net work done (in calories) by 1 mole of monatomic ideal gas in a process described by
1, 2,3, 4 in given V-T graph .

Use : ` R = 2 cal //"mole K"`
`ln 2= 0.7`
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume `V_1` and contains ideal gas at pressure `P_1` and temperature `T_1`.The other chamber has volume `V_2` and contains ideal gas at pressure `P_2` and temperature `T_2`. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionOne mole of an ideal gas is allowed to expand reversible and adiabatically from a temperatureof`27^(@)C)`if the work done during the process is`3`kJ,the final temperature will be equal to`(C_(v)=20JK^(-1))`
View SolutionA gas `(C_(v.m)=(5)/(2)R)` behaving ideally was allowed to expand reversibly and adiabatically from 1 liter to
32 liter . It's initial at temperature was `327^(@)` C . The molar enthalpy changes `("in "J//"mole")` for the process is
View SolutionTwo moles of an ideal gas `(C_(V) = (5)/(2)R)` was compressed adiabatically against constant pressure of 2 atm .
Which was initially at 350 K and 1 atm pressure. The work involve in the process is equal to.
View SolutionA diatomic ideal gas initially at 273 K is given 100 cal heat due to which system did 209 J work.
Molar heat capacity ` (C_(m))`n of gas for the process is :
View SolutionFor an ideal monoatic gas during any process `T= kV`, find out the molar heat capacity od the gas
during the process. (Assme vibrational degree of freedom to be active )\
View SolutionThe maximum efficiency of a heat engine operating between ` 100 ^(@)` and ` 25^(@)` C is
View SolutionA heat engine operating n between ` 227^(@)` and ` 27^(@) C` absorbs 2 K a cal of heat from the ` 227^(@)` reservoir
reversibly per cycle . The amount of work done in one cycle is
View SolutionA reversible heat engine A(based on carnot cycle ) absorbs heat from a reservoir at 1000 K and rejects heat to a reservoir at `T_(2)` . A second reserviour at `T_(2)` and rejects energy to a reservoir at 360 K . If the efficiencies of engines A and B are the same then the temperature `T_(2)`is .
View SolutionThe entropy change when two of ideal monoatomic gas is heated form `200 to 300^(@)C` reversiblity and isochorically?
View SolutionWhat can be concluded about the values of `DeltaH` and `DeltaS` from this graph ?
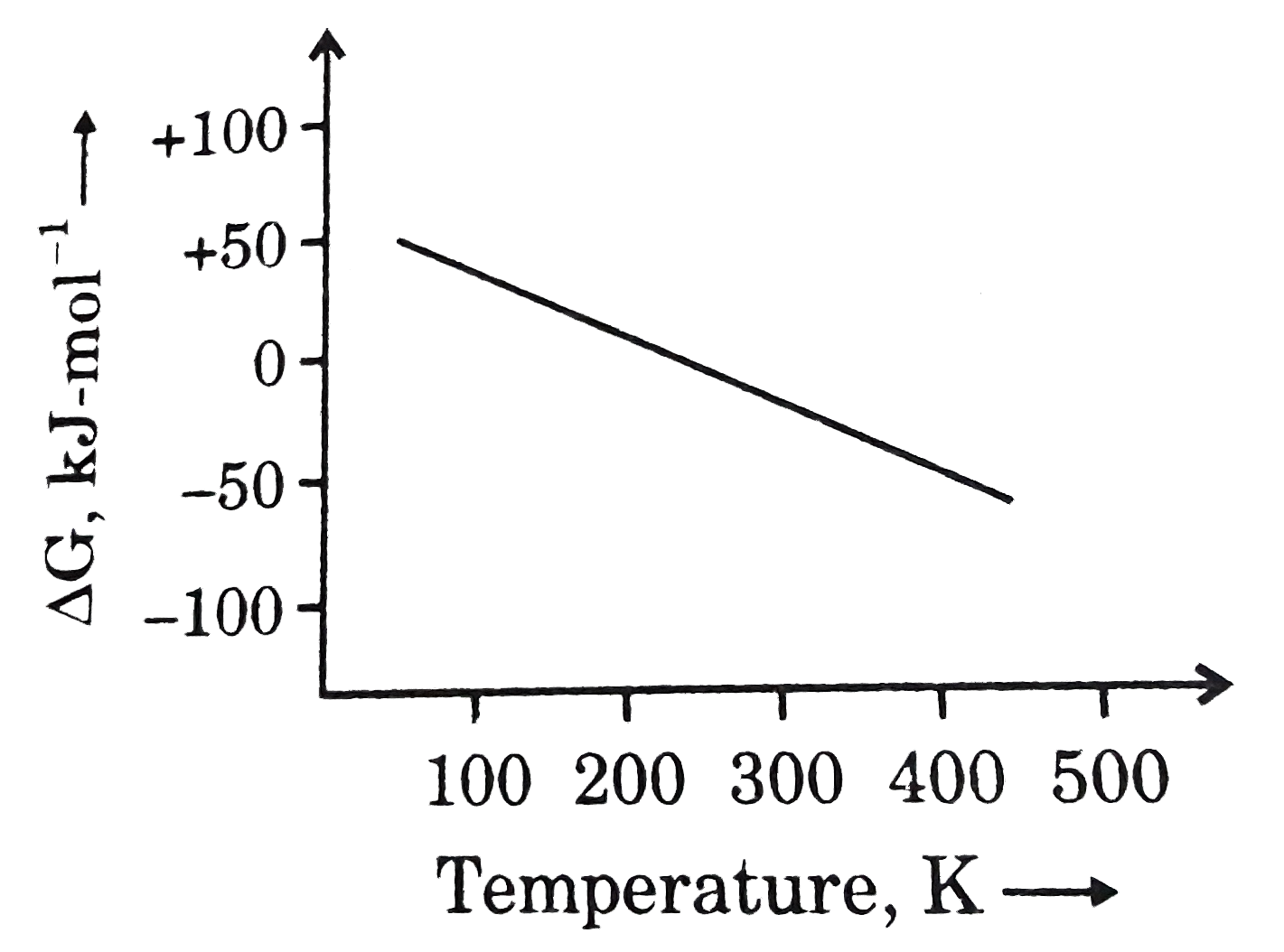
View SolutionIf `DeltaH_("vaporisation")` of substance X (l) (molar mass :30 g/mol) is 300 J/g at it's boiling piont 300K, then
molar entropy change for reversible conddensation process is
View SolutionThe change in entrophy of 2 moles of ideal gas upon isothermal expansion at `243.6 K` from 20 liter until
the pressure becomes 1 atm, is :
View SolutionPressure of 10 moles of an ideal gas is changed from 2 atm to 1 at against constant external pressure without change in temperature. If surrounding temperature (300K) and pressure (1 atm) always remains constant then calculate total entropy change `(DeltaS_("system")+DeltaS_("surrounding"))` for given process.
[Given : ? n2 = 0.70 and R = 8.0 J/mol/K]
View SolutionThe enthalpy of tetramerization of X in gas phase `(4 X(g) to X_(4)(g))` is -100 kJ/mol at 300K.
The enthalpy of vaporisation for liquid X and `X_(4)` are respectively `30kJ//mol` and `72kJ//mol` respectively .
`DeltaS` for tetramerization of X in liquid phase is - 125J/K mol at 300K.
What is the `DeltaG` at 300n K for tetramerization of X liquid phase ?
View SolutionStandard enthorpy of ` X_(2), Y_(2)` and `XY_(3)` are 60,40 and ` 50 JK^(-1) mol^(-1)`, respectively . For the reaction ,
`(1)/(2)X_(2)+(3)/(2)Y_(2) to XY_(3), DeltaH = - 30 kJ` to be at equilibrium, the temperature of will be
View SolutionFor the f reaction at `300K`
`A(g)+B(g) to C(g)`
`DeltaU = - 3.0 k cal" "," "DeltaS = - 10.0 cal //K`
Value of the `DeltaG` is
View SolutionThe correct relationship between free energy change in a reaction and the corresponding equilibrium
constant K is
View SolutionThe value of `DeltaG_(f)^(@)` of gaseous mercury is `31 K J //"mole"`. At what total external pressure mercury start
boiling at `25^(@)C`. `[R=8.3 J// "K mole"]`
View SolutionWhat is `Delta_(r)G`(KJ/mol) for sysnthesis of ammonia at 298K at following sets of partial pressure:
`N_(2)(g) + 3H_(2)(g) hArr 2NH_(3) , Delta_(r) G^(@) = - 33 KJ//mol`.`[Take R= 8.3J//K "mole", log2 = 0.3, log3= 0.48]`
`underset("Pressure(atm)")(Gas)" "underset(1)(N_(2))" "underset(3)(H_(2))" "underset(0.02)(NH_(3))`
View SolutionFor the reaction takes places at certain tempreature `NH_(4) HS(s) hArrNH_(3)(g) + H_(2)S(g)`,
if eqilibrium pressure is X bar, then `Delta_(r) G^(@)` would be
View SolutionCalculate `log_(10){[C]_(eq)//[A]_(eq)}` where [C] and [A] are equilirium molar concetration of respective
species, when 2 2 mole each of A and B were allowed to come to equilibrium at 900 K.
`A + B overset(900 K) hArrC + D" ", " "DeltaG^(@) = 460.6 "Calorie"`
Take: `underset(R=2 Cal //K"mole")(ln X = 2.303 log X)`
View SolutionWhat is the free energy charge `(DeltaG)` when 1.0 mole of water at `100^(@)C` and 1 atm pressure is converted
into steam at ` 100^(@)C` and 1 atm pressure ?
View SolutionWhat is the free energy charge `(DeltaG)` when 1.0n mole of water at ` 100^(@)C` and 1 atm pressue is converted
into steam at `100^(@)C` and 2 atm pressure ?
View Solution
Exercise 1 questions and complete solutions for chapter THERMODYNAMICS of BANSAL CHEMISTRY (HINGLISH) of Class 12