Complete Solutions to EXERCISE-3 (SECTION-A) (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS) (MONOTONICITY) of chapter APPLICATION OF DERIVATIVE of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATION OF DERIVATIVE |
| BANSAL HINDI | EXERCISE-3 (SECTION-A) (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS) (MONOTONICITY) |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
माना फलन `g: ( - oo, oo ) rarr ( - ( pi )/(2) , ( pi )/( 2))` जो `g( u ) = 2 tan^(-1) ( e^(u)) - ( pi )/(2)` द्वारा दिया जाता है, तो g है
View Solutionमाना `f(x)` एक अचरेतर (non-constant), दो बार अवकलनीय फलन है जो `(-oo, oo)` पर इस प्रकार परिभाषित है कि `f(x) = f(1 - x)` तथा `f'((1)/(4) ) =0` है, तब -
View Solutionफलन `f(x) = x cos "" (1)/(x) , x ge1 ` के लिये
View Solutionमाना कि वास्तविक मानों वाला फलन अन्तराल `(0, oo)` पर `f(x) = l nx + int_(0)^(x) sqrt( 1+ sin t) dt` द्वारा परिभाषित है। तो निम्न में से कौन से वक्तव्य सत्य है?
View Solutionप्रश्न 23 और 24 के लिए अनुच्छेद
माना कि `f(x) = (1-x)^(2) sin^(2) x + x^(2)` जहाँ `x in R` और `g(x) = int_(1)^(x) ((2( t-1) )/( t+1) - lnt ) f(t) dt`, जहाँ `x in (1,oo)`
दिये गये कथन हैं:
P: एक ऐसी संख्या `x in RR` का अस्तित्व है जिसके लिए `f(x) + 2x = 2 (1 + x^(2) ) `
Q: एक ऐसी संख्या `x in RR` का अस्तित्व है जिसके लिए `2f(x) + 1= 2x ( 1+ x)`
तब निम्न में से कौनसा कथन सही?
View Solutionप्रश्न 23 और 24 के लिए अनुच्छेद
माना कि `f(x) = (1-x)^(2) sin^(2) x + x^(2)` जहाँ `x in R` और `g(x) = int_(1)^(x) ((2( t-1) )/( t+1) - lnt ) f(t) dt`, जहाँ `x in (1,oo)`
निम्न में से कौन सा कथन सही है ?
View Solution`( - oo, oo)` में बिंदुओं कि संख्या, जिनके लिए `x^(2) - x sin x - cos x = 0 ` ,है `: (1) 6 (2) 4 (3) 2 (4) 0`
View Solutionमाना कि `f(x) = x sin pi x, x gt 0`, तब सभी घन-पूर्णांकों `n` के लिए `f'(x)` निम्न पर शून्य होता है :
View Solutionमाना `f: (0,oo)to R` निम्न के द्वारा `f(x) =int_(1/x)^xe^(-(t+1/t))dt/t`परिभाषित है | तब,
View Solutionमाना कि `f,g:[-1,2]toR` सतत फलन है जो कि अंतराल (-1,2) में दो बार अवकलनीय है। माना कि f और g के मान, बिदुओं -1,0 और 2 पर निम्न सारणी में दर्शाए गए है

यदि प्रत्येक अंतराल (-1,0) और (0,2) में फलन `(f-3g)"` कभी भी शून्य का मान नहीं लेता है तब सही कथन है
View Solutionमाना कि `F:R rarr R` एक फलन है जो तीन बार अवकलनीय (thrice differentiable) है। माना कि F(1) = 0, F(3)=-4 और सभी `x in (1//2,3) ` के लिए `F'(x)<0` है। माना कि सभी `x in R` के लिए f(x) = xF(x) है।
निम्नलिखित में से सही कथन है (हैं)
View Solutionमाना कि `F:R rarr R` एक फलन है जो तीन बार अवकलनीय (thrice differentiable) है। माना कि F(1) = 0, F(3)=-4 और सभी `x in (1//2,3) ` के लिए `F'(x)<0` है। माना कि सभी `x in R` के लिए f(x) = xF(x) है।
यदि `int_(1)^(3) x^(2)F'(x)dx=-12` और `int_1^3x^(3)F''(x)dx = 40` , है, तब सही कथन है (हैं)
View Solutionमाना कि `F : R rarr R ` एक फलन है जो तीन बार अवकलनीय है। माना कि `F(1) = 0, F ( 3) = -4` और सभी `x in ((1)/(2) , 3)` के लिये, `F'(x) lt 0` है। माना कि सभी `x in R ` के लिए , `f(x) = x F(x) ` है।
यदि और सभी हैं, तब के लिए का न्यूनतम मान क्या होगा ?
View Solutionऐसी सभी भिन्न (distinct) `x""in[0,1]` जिनके लिए `int_(0)^(x)(t^(2))/(1+t^(4))dt=2x-1` है, कि कुल संख्या है
View Solutionनीचे दी गयी टेबल के तीन कॉलमों में उपलब्ध सुचना का उपयुक्त ढंग से सुमेल कर प्रश्नों एवं के उत्तर दीजिये।
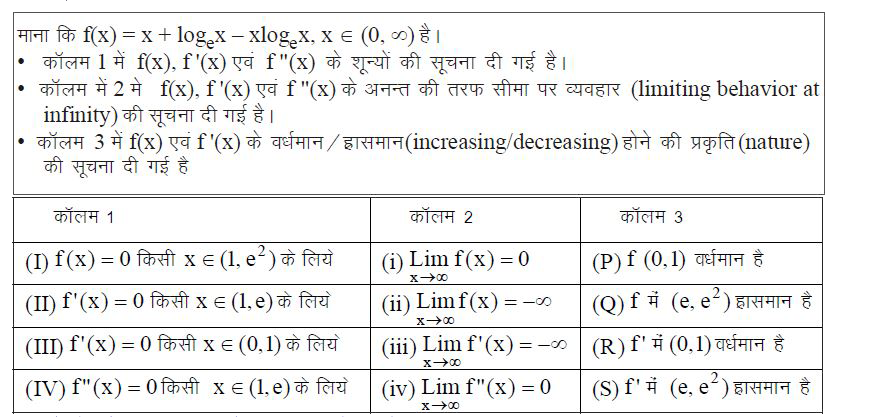
निम्न में से कौन सा विकल्प केवल सही संयोजन है ?
View Solutionनीचे दी गयी टेबल के तीन कॉलमों में उपलब्ध सुचना का उपयुक्त ढंग से सुमेल कर प्रश्नों एवं के उत्तर दीजिये।
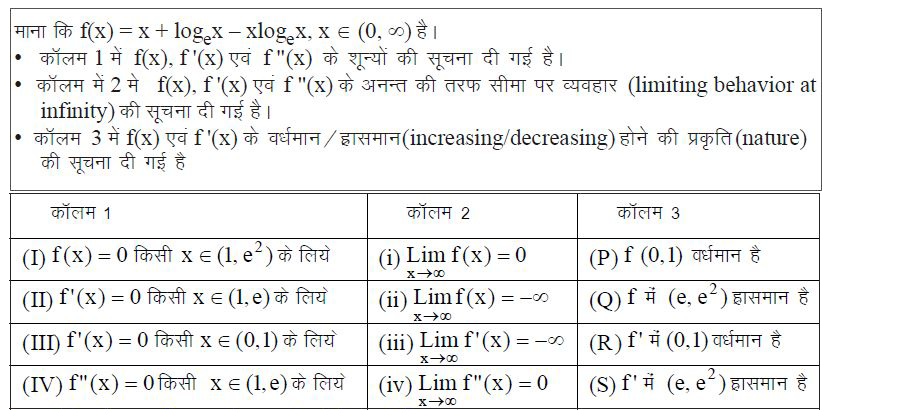
निम्न में से कौन सा विकल्प केवल सही संयोजन है ?
View Solutionनिम्न का मिलान कीजिए।
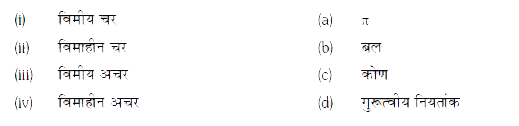
View Solutionयदि `f:RtoR` इस प्रकार का एक द्विअवकलनीय फलन है कि सभी `x epsilon R` के लिए `f"(x)gt0` एवं `f(1/2)=1/2,f(1)=1,` है तब
View Solutionयदि `f: R rarr R ` इस प्रकार अवकलनीय फलन है कि सभी `x in R ` के लिये `f'(x) gt 2f(x) `, एवं `f(0) = 1` है , तब
View Solution
EXERCISE-3 (SECTION-A) (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS) (MONOTONICITY) questions and complete solutions for chapter APPLICATION OF DERIVATIVE of BANSAL MATHS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 MATHS APPLICATION OF DERIVATIVE
- EXERCISE -4 SECTION-B(POTENTIAL PROBLEM BASED ON CBSE)
- EXERCISE -4( SECTION -A) ( CBSE PREVIOUS YEAR.S QUESTIONS)
- EXERCISE-1 SECTION -B[MONOTONICITY] (SPECIAL DPP-1)
- EXERCISE-1 SECTION -B[MONOTONICITY] (SPECIAL DPP-2)
- EXERCISE-1 SECTION -B[MONOTONICITY] (SPECIAL DPP-3)
- EXERCISE-1 SECTION-C[MAXIMA & MINIMA ](SPECIAL DPP-1)
- EXERCISE-1 SECTION-C[MAXIMA & MINIMA ](SPECIAL DPP-2)
- EXERCISE-1 SECTION-C[MAXIMA & MINIMA ](SPECIAL DPP-3)
- EXERCISE-1 ( SECTION-A [ TANGENT & NORMAL] (SPECIAL DPP -2)
- EXERCISE-1 ( SECTION-A [ TANGENT & NORMAL] (SPECIAL DPP-1)
- EXERCISE-2 (SECTION-A[TANGENT & NORMAL ]
- EXERCISE-2 SECTION-B [ MONOTONICITY] (SPECIAL DPP-1)
- EXERCISE-2 SECTION-B [ MONOTONICITY] (SPECIAL DPP-2)
- EXERCISE-2 SECTION-C[MAXIMA & MINIMA ]
- EXERCISE-3 (SECTION-A) (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS) ( TANGENT AND NORMAL)
- EXERCISE-3 (SECTION-A) (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS) (MAXIMA & MINIMA)
- EXERCISE-3 (SECTION-A) (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS) (MONOTONICITY)
- EXERCISE-3 SECTION-B (JEE-MAIN PREVIOUS YEAR.S QUESTIONS) ( TANGENT AND NORMAL)
- EXERCISE-3 SECTION-B (JEE-MAIN PREVIOUS YEAR.S QUESTIONS) (MAXIMA & MINIMA)
- EXERCISE-3 SECTION-B (JEE-MAIN PREVIOUS YEAR.S QUESTIONS) (MONOTONICITY)
- EXERCISE-5(RANK BOOSTER)