Complete Solutions to EXERCISE-1 (SPECIAL DPP-3) of chapter COMPLEX NUMBER of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | COMPLEX NUMBER |
| BANSAL HINDI | EXERCISE-1 (SPECIAL DPP-3) |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
चित्र में सम्मिश्र समतल में कुछ संख्याऐं दर्शायी गयी है तथा वृत्त एक इकाई वृत्त है जिसका केन्द्र मूल बिन्दु है, तब निम्न में से कौनसा एक F का प्रतिलोम होगा
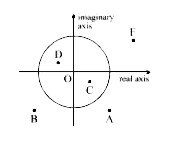
View Solutionयदि z= x + iy & `omega = (1-iz)/(z-i)` तब `|omega| = 1` सम्मिश्र तल में दर्शाते है -
View Solutionसम्मिश्र तल में असमिका `2 lt= |z-1| lt 3` को सन्तुष्ट करने वाले एक बिन्दु z का बिन्दुपथ निरूपित करता है।
View Solutionयदि arg `z = - pi//3` है तब z का बिन्दु पथ है -
View Solutionमाना z सम्मिश्र संख्या इस प्रकार है कि arg (z - 2 ` = (2pi)/(3)` एवं |z| = 2 है, तो z के कोणांक का मुख्य मान है
View Solutionयदि `z_1` और `barz_1` किसी n भुजा वाले समबहुभुज के आसन्न शीर्ष है जिसका केन्द्र मूल बिन्दु है। यदि `(Im z_1)/(Re z_1) = sqrt2 - 1` है, तो n का मान बराबर है
View Solutionमाना z=x + iy, जहाँ `x, y in R` और `i= sqrt(-1)` है।`Re(1/z) = 1/2` को संतुष्ट करने वाले P(z) का बिन्दुपथ एक वृत्त को प्रदर्शित करता है, तो बिन्दु M (-2, 4) की वृत्त पर स्थित किसी बिन्दु से अधिकतम दूरी होगी [Re(z) सम्मिश्र संख्या z के वास्तविक भाग को प्रदर्शित करता है]
View Solutionx के वे सभी वास्तविक मान जो असमिका `|1+4i-2^(-x)| lt= 5` जहाँ `i = sqrt(-1), x in R` को सन्तुष्ट करते है, होगे: (i) `[-2,oo)` (ii) `(-oo,2]` (iii) `[0,oo)` (iv) `[-2,0]`
View Solution`Z_1 = root(6)((1-i)/(1+isqrt3) ), Z_2 = root(6)((1-i)/(sqrt3+i)), Z_3 = root(6)((1+i)/(sqrt3 - i))` के लिए सत्य कथन है -
View Solutionसमीकरण `z^3 +iz - 1 = 0` के वास्तविक या पूर्णतः काल्पनिक हलों की कुल संख्या हैं :
View Solutionयदि 'z', वक्र | z-4-3i| = 2 पर स्थित है, तब |z| का अधिकतम व न्यूनतम मान है -
View Solutionयदि सम्मिश्र तल में समीकरण | z +i|+ | z-i| = 8 को सन्तुष्ट करता है तब | z | का अधिकतम मान होगा -
View Solutionमाना सम्मिश्र संख्याएँ `z_r (1 lt= r lt= 4)` इस प्रकार है कि `| z_r | = sqrt(r+1)` और `|30z_1 + 20z_2 + 15z_3 +12z_4| = k|z_1z_2z_3 + z_2z_3z_4 + z_3z_4z_1 + z_4z_1z_2|` है, तो k का मान बराबर है
View Solution
EXERCISE-1 (SPECIAL DPP-3) questions and complete solutions for chapter COMPLEX NUMBER of BANSAL MATHS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 MATHS COMPLEX NUMBER
- EXERCISE-1 (SPECIAL DPP-1)
- EXERCISE-1 (SPECIAL DPP-2)
- EXERCISE-1 (SPECIAL DPP-3)
- EXERCISE-1 (SPECIAL DPP-4)
- EXERCISE-1 (SPECIAL DPP-5)
- EXERCISE-1 (SPECIAL DPP-6)
- EXERCISE-1 (SPECIAL DPP-7)
- EXERCISE-2
- EXERCISE-3 (SECTION-A (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS))
- EXERCISE-3 (SECTION-B (JEE-MAIN PREVIOUS YEAR.S QUESTIONS))
- EXERCISE-4 (POTENTIAL PROBLEMS BASED ON CBSE)
- EXERCISE-5 (RANK BOOSTER)