Complete Solutions to Exercise -1 Special DDP-5 [LIMIT] of chapter फलन की सीमा सत्त्यता तथा अवकलनीयता of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | फलन की सीमा सत्त्यता तथा अवकलनीयता |
| BANSAL HINDI | Exercise -1 Special DDP-5 [LIMIT] |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
निम्नलिखित में से कौन सा फलन `f(x)=underset(n to oo)Lim (x^(2n)-1)/(x^(2n)-1)` के समरूप है।
03:38View Solutionचित्र में दर्शाया गया समद्विबाहु त्रिभुज ABC जिसमें `angleB= angleC` है। कोण B का कोर्णाधक भुजा AC को बिन्दु P पर प्रतिच्छेद करता है। मान लिजिये BC नियत है तथा लम्ब AM शून्य की ओर जा रहा है इस प्रकार `A to M` (BC का मध्य बिन्दु). BP का सीमित मान क्या होगा-
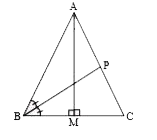
जहाँ a नियत भुजा BC है।03:33View Solution`underset(x to oo)Lim (((x+1)^(x))/(x^(x).e))^(x)` बराबर है
05:14View Solution`underset(n to oo)Lim (sqrt(n^(2)+n+1)-[sqrt(n^(2)+n+1)]) (n in I)` जहाँ [] एक महत्तम पूर्णांक फलन है, बराबर है-
02:59View Solution`underset(n to oo)Lim (1^2n+2^2 (n-1) +3^2 (n-2)+…..+n^2)/(1^3+2^3+3^3+….+n^3)` का मान होगा-
04:23View Solutionमाना `f(x)=tan^(-1) ((sqrt(1+x^2)-1)/x)" तथा "g(x)="cosec"^(-1) (sqrt(1+x^2)/x), x ne 0`
समीकरण `x^2=|f(x)-g(x)|` के हल/हलो की संख्या है05:32View Solutionमाना `f(x)=tan^(-1) ((sqrt(1+x^2)-1)/x)" तथा "g(x)="cosec"^(-1) (sqrt(1+x^2)/x), x ne 0`
यदि `f(x)+g(x)=pi/8` है, तो x का मान है09:34View Solutionमाना `f(x)=tan^(-1) ((sqrt(1+x^2)-1)/x)" तथा "g(x)="cosec"^(-1) (sqrt(1+x^2)/x), x ne 0`
`underset(x to 0)Lim [6(f(x)+g(x))/(x)]` का मान है
[f Vli. Kh : [k], k से छोटे या बराबर महत्तम पूर्णाक को निरूपित करता है।]08:03View Solutionमाना `f(x)={{:(,(x)/(tan x), -oo lt x lt 0),(,2,x=0),(,(ln (1+2x))/(x), 0 lt x lt oo):}" तथा "g(x)={{:(,x+4, -oo lt x lt 1),(,x^2-5x+11, 1 le x lt 2),(,x-3, 2le x lt oo):}` तो निन्न कौन (से) कथन सही है?
08:53View Solutiony=f(x) का आरख दर्शाया गया है, तो निम्न में कौन (से) सही है? [[k] एवं {k} क्रमशः महत्तम पूर्णाक एवं भिनाश भाग फलन है]
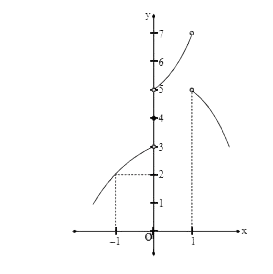 View Solution
View Solution View Solution
View Solutionc के किसी मान के लिए `underset(x to -oo)Lim [(x^5+7x^4+2)^C-x]` परिमित तथा अशून्य है तथा इसका मान l है, तो (l-2c) का मान होगा।
06:06View Solutionयदि `underset(x to 0)Lim (1+a cos 2x+b cos 4x)/x^4` का सभी `x in R` के लिए मान c के बराबर हो, तो 3(a+b+c) का मान ज्ञात कीजिए।
06:53View Solutionमाना `underset(x to oo)Lim x ln (e(1+1/x)^(1-x))` का मान `m/n` है, जहाँ m तथा n सापेक्षिक अभाज्य धनात्मक पूर्णाक है, तो (m+n)का मान ज्ञात कीजिये।
03:41View Solution
Exercise -1 Special DDP-5 [LIMIT] questions and complete solutions for chapter फलन की सीमा सत्त्यता तथा अवकलनीयता of BANSAL MATHS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 MATHS फलन की सीमा सत्त्यता तथा अवकलनीयता
- Exercise -1 Special DDP-10 [DERIVABILITY]
- Exercise -1 Special DDP-7 [CONTINUITY]
- Exercise -1 Special DDP-8 [DERIVABILITY]
- Exercise -1 Special DDP-9 [DERIVABILITY]
- Exercise -1 (Special DDP-1 [LIMIT])
- Exercise -1 Special DDP-2 [LIMIT]
- Exercise -1 Special DDP-5 [LIMIT]
- Exercise -1 Special DDP-6 [CONTINUITY]
- Exercise -1 Special DPP-3 [LIMIT]
- Exercise -1 Special DPP-4 [LIMIT]
- Exercise -1 सत्य एव असत्य
- Exercise -2 Section -A [Limit]
- Exercise -2 Section -B [CONTINUITY]
- Exercise -2 Section -C [DERIVABILITY]
- Exercise -3 (Section -A)
- Exercise -3 Continuity And Differentiability
- Exercise -3 Section -B (LIMITS)
- Exercise -4 (Section -A)
- Exercise -4 SECTION-B
- Exercise -5 (Rank Booster)
