Complete Solutions to ILLUSTRATION of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| BANSAL HINDI | ILLUSTRATION |
| Number Of Questions | 44 |
| Academic Year | 2023-24 |
दो सिक्कें (एक रूपयें एवं दो रूपयें का एक-एक सिक्का) एक बार उछाले जाते है। प्रतिदर्श समष्टि ज्ञात कीजिये।
01:43View Solutionएक सिक्का दो बार उछलता जाता है. यदि द्वितीय फेक में पुच्छ प्राप्त होता है तब पासा प्रक्षिप्त किया जाता है. एक घटना का प्रतिदर्श समष्टि लिखिए .
01:06View Solutionएक पांसे युग्म की उछाल में दो सम्भव घटनाऐं लिखिए। जबकि
`E_1` = दोनों पांसों पर संख्याओं का योग 7 है।
` E_2` = दोनों पांसों पर संख्याओं का योग 3 से भाज्य है।07:24View Solutionएक पासे की उछाल के प्रयोग पर विचार कीजिये। माना A एक घटना 'अभाज्य संख्या का प्राप्त होना' है तथा B एक घटना ' विषम संख्या प्राप्त होना' है, तो निम्न घटनाओं को निरूपित करने वाले समुच्चय ज्ञात कीजिये। (i) A या B (ii) A तथा B (iii) A परन्तु B नहीं (iv) A नहीं
03:50View Solutionएक वृद्ध व्यक्ति सात अंकों के फोन नम्बर को डायल करता है, इनमें से पाँच अंकों को डायल करने के पश्चात् अचानक अन्तिम दो अंकों को भूल जाता है परन्तु उसे ज्ञात है कि अन्तिम दोनों अंक भिन्न-भिन्न है। इस तथ्य के आधार पर वह यादृच्छया दोनों अन्तिम अंकों को डायल करता है, तो सही टेलिफोन डायल होने की प्रायिकता ज्ञात कीजिये।
01:56View Solutionप्रथम 20 प्राकृत संख्याओं में से यादृच्छाया दो प्राकृत संख्याओं का चयन किया जाता है। निम्न प्रायिकता ज्ञात कीजिये।
उनका योगफल विषम है।03:20View Solutionप्रथम 20 प्राकृत संख्याओं में से यादृच्छाया दो प्राकृत संख्याओं का चयन किया जाता है। निम्न प्रायिकता ज्ञात कीजिये।
उनका योगफल सम है।03:55View Solutionप्रथम 20 प्राकृत संख्याओं में से यादृच्छया दो प्राकृत संख्याओं का चयन किया जाता है। निम्न प्रायिकता ज्ञात कीजिये।
चयनित युग्म एक युग्म अभाज्य हो।01:50View Solutionकिसी लिप ईयर में 53 रविवार के होने की प्रायिकता ज्ञात कीजिए ।
03:42View Solutionयादृच्छया एक लीप वर्ष का चयन किया जाता है, इसमें निम्न के होने की प्रायिकता ज्ञात कीजिये।
53 रविवार तथा सोमवार02:58View Solutionयादृच्छया एक लीप वर्ष का चयन किया जाता है, इसमें निम्न के होने की प्रायिकता ज्ञात कीजिये।
53 रविवार या 53 सोमवार04:15View Solution5 विभिन्न कंचों को यादृच्छिक रूप से 5 विभिन्न बॉक्स में रखा जाता है। ठीक दो बॉक्सों के रिक्त रहने के पक्ष में संयोगानुपात ज्ञात कीजिये। दिया गया है कि प्रत्येक बॉक्स में कितनी भी संख्या में कंचें रखे जा सकते है।
05:28View Solutionदो विद्यार्थी अनिल एवं अशिमा एक परीक्षा में बैठते है। अनिल के परीक्षा उत्तीर्ण करने की प्रायिकता 0.05 है जबकि अशिमा के एक परीक्षा उत्तीर्ण करने की प्रायिकता 0.10 है। दोनों के परीक्षा उत्तीर्ण करने प्रायिकता 0.02 है, तो प्रायिकता ज्ञात कीजिये कि
अनिल एवं अशिमा दोनों ही परीक्षा उत्तीर्ण नही करे।03:29View Solutionदो विद्यार्थी अनिल एवं अशिमा एक परीक्षा में बैठते है। अनिल के परीक्षा उत्तीर्ण करने की प्रायिकता 0.05 है जबकि अशिमा के एक परीक्षा उत्तीर्ण करने की प्रायिकता 0.10 है। दोनों के परीक्षा उत्तीर्ण करने प्रायिकता 0.02 है, तो प्रायिकता ज्ञात कीजिये कि
कम से कम एक परीक्षा में उत्तीर्ण नहीं हो।03:05View Solutionदो विद्यार्थी अनिल एवं अशिमा एक परीक्षा में बैठते है। अनिल के परीक्षा उत्तीर्ण करने की प्रायिकता 0.05 है जबकि अशिमा के एक परीक्षा उत्तीर्ण करने की प्रायिकता 0.10 है। दोनों के परीक्षा उत्तीर्ण करने प्रायिकता 0.02 है, तो प्रायिकता ज्ञात कीजिये कि
उनमें से केवल एक ही परीक्षा उत्तीर्ण करे।03:35View Solutionएक कक्षा में, भौतिकी में अनुत्तीर्ण विद्यार्थी 30%, गणित में अनुत्तीर्ण विद्यार्थी 25% तथा भौतिकी एवं गणित दोनों में अनुत्तीर्ण विद्यार्थी 15% है। यदि यादृच्छिक चुना गया विद्यार्थी गणित में अनुत्तीर्ण है, तो उसके भौतिकी में भी अनुत्तीर्ण होने की प्रायिकता ज्ञात कीजिये।
03:06View Solutionमाना A तथा B दो घटनायें इस प्रकार है कि P(A) = 0.3, P(B) = 0.6 है तथा `P((B)/(A))=0.5` है, तो `P((bar(A))/(barB))` का मान है
04:33View Solutionएक पांसे को उछालने पर घटना E' प्रकट होने वाली संख्या 3 की गुणज है ' तथा घटना F 'प्रकट होने वाली संख्या सम है' तब ज्ञात कीजिये कि घटना E तथा F स्वतन्त्र है।
02:57View Solutionतीन सिक्कों को एक साथ उछाला जाता है। घटना E'तीन पट् या तीन चित' तथा घटना F'कम से कम दो पट्' एवं घटना G'अधिकतम दो पट ' पर विचार कीजिये। युग्मों (E, F), (E, G) तथा (EG) में से कौनसी स्वतन्त्र है? कौनसी परतन्त्र है।
08:16View Solutionदी गई चार मशीनों में दो ठीक और दो खराब है। इन मशीनों का एक एक करके यादृच्छिक क्रम में तब तक परीक्षण किया जाता है जब तक दोनों खराब मशीनें पहचान ली न जायें। केवल दो ही परीक्षणों की आवश्यकता होगी, इस बात की प्रायिकता होगी
02:46View SolutionA, Bएवं C किसी शहर के तीन समाचार पत्र है। 25% जनसंख्या A पढ़ती है, 20% जनसंख्या B पढ़ती है, 15% जनसंख्या C पढ़ती है, 12% जनसंख्या A एवं B पढ़ती है, 10% जनसंख्या B एवं C पढ़ती है, 6% जनसंख्या A एवं C पढ़ती है तथा 4% सभी तीन समाचार पत्र पढ़ती है, तो A, Bएवं C में से कम से कम एक समाचार पत्र पढ़ने वाली जनसंख्या का प्रतिशत ज्ञात कीजिये।
03:48View Solutionमाना A, B एवं C तीन घटनायें इस प्रकार है कि
p=P(A या B में ठीक एक) = P(B या C में से ठीक एक) =PIC या A में से ठीक एक) तथा PLA, B, C एक साथ) =`p^2` जहाँ `0 lt p lt 1/2` है, तब P (A, B या C में से कम से कम) का मान है05:37View Solutionएक पांसा युग्म को 6 बार उछाला जाता है, एक द्विक प्राप्त करना सफलता है, निम्न की प्रायिकता ज्ञात कीजिये।
कोई सफलता नहीं03:50View Solutionएक पांसा युग्म को 6 बार उछाला जाता है, एक द्विक प्राप्त करना सफलता है, निम्न की प्रायिकता ज्ञात कीजिये।
ठीक एक सफलता04:12View Solutionएक पांसा युग्म को 6 बार उछाला जाता है, एक द्विक प्राप्त करना सफलता है, निम्न की प्रायिकता ज्ञात कीजिये।
कम से कम एक सफलता04:28View Solutionएक पांसा युग्म को 6 बार उछाला जाता है, एक द्विक प्राप्त करना सफलता है, निम्न की प्रायिकता ज्ञात कीजिये।
अधिकतम एक सफलता03:56View Solutionदो थैलों में से प्रथम थैले में 5 सफेद एवं 3 काली गेंदे है एवं द्वितीय थैले में 3 सफेद एवं 5 काली गेंदें है। प्रथम थैले से यादृच्छया दो गेंदें निकालकर बिना रंग देखे द्वितीय थैले में रख दी जाती है। अब द्वितीय थैले से दो गेंदे निकाली जाती है, तो निकाली गई गेंदो का सफेद एवं काली होने की प्रायिकता ज्ञात कीजिये।
09:41View Solutionदो मशीने A तथा B एक कारखाने में क्रमश: 60% एवं 40% वस्तुओं का उत्पादन करती है। इन मशीनों द्वारा खराब उत्पादन की प्रायिकता क्रमश: 2% एवं 5% है। यदि एक वस्तु का यादृच्छया चयन किया जाता है, तो चयनित वस्तु (i) खराब (ii) खराब नहीं होने की प्रायिकता ज्ञात कीजिये।
03:53View Solutionथैले.A में 3 सफेद एवं 2 काली गेंदे है। थैले B में 2 सफेद एवं 2 काली गेंदे है। यादृच्छया थैले A से एक गेंद निकालकर थैले B में स्थानान्तरित की जाती है। थैले B से यादृच्छया एक गेंद का चयन किया जाता है जो कि सफेद है, तो स्थानान्तरित की गई गेंद के सफेद होने की प्रायिकता ज्ञात कीजिये।
04:36View Solutionएक पत्र या तो LONDON से या CLIFTON से आया है। पत्र पर लगाई गई मोहर पर गलती से दो क्रमागत अक्षर "ON" छपा है, तो पत्र के LONDON से आने की प्रायिकता ज्ञात कीजिये
05:33View Solutionएक बोल्ट बनाने के कारखाने में, मशीने A,B,C कुल उत्पाद का क्रमशः 25%, 35% तथा 40% बोल्ट बनाती है। इन मशीनों के उत्पादन का क्रमशः 5,4 तथा 2 प्रतिशत भाग दोषयुक्त है। बोल्टों के कुल उत्पादन में से एक बोल्ट यादृच्छया निकाला जाता है और वह दोषयुक्त पाया जाता है। इसकी क्या प्रायिकता है कि वह बोल्ट मशीर B द्वारा बनाया गया है?
04:44View Solutionएक परीक्षा में एक विद्यार्थी एक चार विकल्पों वाले बहुविकल्पीय प्रश्न के उत्तर का या तो अनुमान लगाता है या नकल करता है या उसका उत्तर जानता है। उसके द्वारा अनुमान लगाने की प्रायिकता `1/3` है और उसके द्वारा उत्तर की नकल करने की प्रायिकता `1/6` है। इस बात की प्रायिकता कि उसका उत्तर सही है जबकि दिया गया है कि उसने उत्तर की नकल की है `1/8` है। इस बार की प्रायिकता ज्ञात कीजिए कि वह प्रश्न का उत्तर जानता था जबकि दिया है कि उसने सही उत्तर दिया है।
05:09View Solutionमाना HIV परीक्षण की विश्वसनीयता निम्न प्रकार निर्दिष्ट की गई। HIV संक्रमित लोगों में, 90% में परीक्षण द्वारा बीमारी का पता लग जाता है परन्तु 10% का पता नहीं लगता है। HIV मुक्त व्यक्तियों में 99% लोगों में HIV-ive तथा 1% HIV +ve ज्ञात किया जाता है। जनसंख्या आधिक्य में से केवल 0.1% लोगों को HIV है। एक व्यक्ति का यादृच्छया चयन किया जाता है। उसको परीक्षण के पश्चात् पेंथोलोजिस्ट बताता है कि वह HIV +ve है, तो व्यक्ति के वास्तविक रूप से HIV संक्रमित होने की प्रायिकता ज्ञात कीजिये।
04:31View Solutionएक बॉक्स में तीन सिक्कें A, B एवं C है।
A : सामान्य सिक्का , B : दो चित वाला सिक्का (DH) , C : एक भारित सिक्का जिससे `P(H) = (1)/(3)`
एक सिक्का यादृच्छया चुना जाता है एवं उछाला जाता है।
चित आने की प्रायिकता ज्ञात कीजिये।04:04View SolutionA : एक बॉक्स में तीन सिक्कें A, B एवं C है।
A : सामान्य सिक्का , B : दो चित वाला सिक्का (DH) , C : एक भारित सिक्का जिससे `P(H) = (1)/(3)`
एक सिक्का यादृच्छया चुना जाता है एवं उछाला जाता है।
यदि चित आता है, तो इसके सामान्य सिक्का P(A/H) होने की प्रायिकता ज्ञात कीजिये।04:37View SolutionA : एक बॉक्स में तीन सिक्कें A, B एवं C है।
A : सामान्य सिक्का , B : दो चित वाला सिक्का (DH) , C : एक भारित सिक्का जिससे `P(H) = (1)/(3)`
एक सिक्का यादृच्छया चुना जाता है एवं उछाला जाता है।
पट् आने की प्रायिकता ज्ञात कीजिये।03:54View Solutionएक बॉक्स में तीन सिक्कें A, B एवं C है।
A : सामान्य सिक्का , B : दो चित वाला सिक्का (DH) , C : एक भारित सिक्का जिससे `P(H) = (1)/(3)`
एक सिक्का यादृच्छया चुना जाता है एवं उछाला जाता है।
यदि पट् आता है, तो इसके भारित सिक्का P(C/T) होने की प्रायिकता ज्ञात कीजिये।03:10View Solution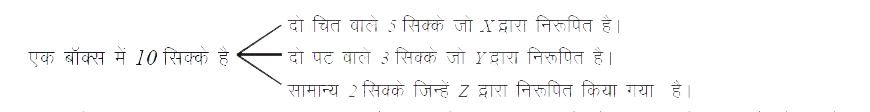
बॉक्स से यादृच्छया एक सिक्का निकाला जाता है तथा उसे उछाला जाता है जो चित रूप में गिरता है, तो इसके सामान्य सिक्का होने की प्रायिकता ज्ञात कीजिए।04:29View Solutionसमान दक्षता के दो खिलाड़ी A तथा B एक खेल खेलते है। वे खेलना छोड़ देते है (किसी असामयिक स्थिति के कारण) जबकि A को जीतने के लिए 3 अंक और B को जीतने के लिए 2 अंक चाहिए होते है। यदि ईनाम की राशि रूपयें 16000 है, तो रेफ्री किस प्रकार धन का विभाजन निष्पक्ष तरीके से कर सकता है।
03:58View Solution5 सफेद एवं 4 लाल गेंदों वाले थैले से प्रतिस्थापन नहीं करते हुए एक-एक करके तीन गेंदें निकाली जाती है, तो निकाली गई लाल गेंदों की संख्या का प्रायिकता बंटन ज्ञात कीजिये।
05:49View Solutionदो खराब अण्डे गलती से 10 अच्छे अण्ड़ों में मिल जाते है। इस टोकरी में से एक साथ 3 अण्डे निकाले जाते है, तो निकाले गये खराब अण्डों का माध्य एवं प्रसरण ज्ञात कीजिये।
05:10View Solutionएक पांसा युग्म को 5 बार उछाला जाता है, यदि द्विक प्राप्त करना एक सफलता माना जाता है, तो सफलताओं का माध्य एवं प्रसरण ज्ञात कीजिये।
13:19View Solutionयदि एक द्विपद प्रायिकता बंटन के माध्य एवं प्रसरण के मध्य अन्तर 1 है तथा वर्गों के मध्य अन्तर 11 है, तो ठीक 3 सफलताएं प्राप्त करने की प्रायिकता ज्ञात कीजिये।
04:49View Solutionयदि 5 परीक्षणों ( trials) के एक द्विपद बंटन के माध्य तथा प्रसरण का योगफल `1*8` है , तो बंटन ज्ञात करें ।
03:43View Solution
ILLUSTRATION questions and complete solutions for chapter PROBABILITY of BANSAL MATHS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 MATHS PROBABILITY
- EXERCISE-1(SPECIAL DPP)(SPECIAL DPP-1)
- EXERCISE-1(SPECIAL DPP)(SPECIAL DPP-2)
- EXERCISE-1(SPECIAL DPP)(SPECIAL DPP-3)
- EXERCISE-1(SPECIAL DPP)(SPECIAL DPP-4)
- EXERCISE-1(SPECIAL DPP)(SPECIAL DPP-5)
- EXERCISE-1(SPECIAL DPP)(SPECIAL DPP-6)
- EXERCISE-1(SPECIAL DPP)(SPECIAL DPP-7)
- EXERCISE-2
- EXERCISE-3 ( SECTION-A ( JEE -ADVANCED PREVIOUS YEAR.S QUESTIONS))
- EXERCISE-3 ( SECTION-B ( JEE -MAIN PREVIOUS YEAR.S QUESTIONS))
- EXERCISE-4 ( SECTION-A (CBSE PREVIOUS YEAR.S QUESTIONS))
- EXERCISE-4 ( SECTION-B (POTENTIAL PROBLEMS BASED IN CBSE))
- EXERCISE-5 (RANK BOOSTER)
- ILLUSTRATION
