Complete Solutions to Exercise -1 (SPECIAL DPP -4) of chapter अनुक्रम तथा श्रेणी of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | अनुक्रम तथा श्रेणी |
| BANSAL HINDI | Exercise -1 (SPECIAL DPP -4) |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
`sum_(k = 0)^(infty) K^(2)/4^(k)` के मान को `m/n` के रूप में लिखा जा सकता है, जहाँ m तथा n सापेक्षिक अभाज्य धनात्मक पूर्णांक है, तो (m +n) का मान है
05:21View Solution`3/1^(3) + 5/(1^(3) + 2^(3)) + 7/(1^(3) + 2^(3) + 3^(3))` + .... का 11 पदों तक का योगफल है
02:56View Solutionमाना `S_(1)=underset(k=1)overset(n)sum K, S_(2)=underset(K=1)overset(n)sum K^2" एवं "S_3=underset(K=1)overset(n)sum K^3` है, तो `(S_(1)^(4) S_(2)^(2)-S_(2)^(2) S_(3)^(2))/(S_(1)^(2)+S_(3)^(2))` का मान है
02:02View Solutionश्रेणी `1/10 + 2/10^(2) + 3/10^(3)` + ...., जिसका nवाँ पद `n/10^(n)` है, का सीमान्त योगफल है
05:06View Solutionव्यंजक `(2^(2) + 4^(2) + 6^(2) + .... + (2n)^(2))/(1^(2) + 3^(2) + 5^(2) + .... + (2n - 1)^(2))` का मान 1.01 से अधिक होने के लिए, n का अधिकतम मान है
04:43View Solutionयदि `a_(1), a_(2), a_(3), ...., a_(n)` एक वर्धमान समान्तर श्रेणी (increasing A.P.) के क्रमागत पद हैं, तथा `(1^(2) - a_(1)) + (2^(2) - a_(2)) + (3^(2) - a_(3)) + .... + (n^(2) - a_(n)) = ((n - 1)^(.) n (n + 1))/3` हो, तो `(a_(5) + a_(3) - a_(2))/6` का मान बराबर है
06:04View Solutionअनन्त श्रेणी `1 + (1 + 1/5)(1/2) + (1 + 1/5 + 1/5^(2))(1/2^(2))` + ....... का योगफल है
02:55View Solutionयदि `S_(n) = underset(r=1)overset(n)sum (2r + 1)/(r^(4) + 2r^(3) + r^(2))` है, तो `S_(10)` का मान है -
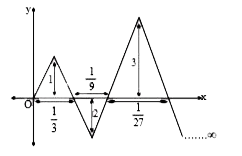
01:57View Solutionदिये गये चित्र में अन्नत त्रिभुजों को बनाया गया है, यदि इन त्रिभुजों का कुल क्षेत्रफल A है तो 8A बराबर होगा
 04:02View Solution
04:02View Solutionमाना `S_(n) = (2 + 2) + (2^(2) + 5) + (2^(3) + 10) + (2^(4) + 17)` + ...... n कोष्ठकों तक है। यदि सभी `n in N` के लिये `S_(n) = 2^(n + A) + Bn^(3) + cn^(2) + Dn + E` है, जहाँ A, B, C, D, E नियतांक है, तो
07:40View Solution`sum_(n = 1)^(infty)1/((3n - 2)(3n + 1)` का मान p/q के बराबर है, जहाँ p तथा q सापेक्षिक अभाज्य प्राकृत संख्याये है तो `(p^(2) + q^(2))` का मान है
05:42View Solutionमाना `f(x) = 5x^(2) - 2x + 26/5` का न्यूनतम मान d है तथा f(x), x = r के सापेक्ष सममित है। यदि `sum_(n = 1)^(infty)(1 + (n - 1)d)r^(n - 1)` का मान है, जहाँ p व q सापेक्षिक अभाज्य है, तो (3q - p) का मान ज्ञात कीजिये।
04:09View Solution
Exercise -1 (SPECIAL DPP -4) questions and complete solutions for chapter अनुक्रम तथा श्रेणी of BANSAL MATHS (HINDI) of Class 12
