Complete Solutions to Exercise -3 (JEE Main Previous Year.s Questions) of chapter MOMENTUM AND COLLISION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOMENTUM AND COLLISION |
| BANSAL HINDI | Exercise -3 (JEE Main Previous Year.s Questions) |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
`m_(1)` व `m_(2)` द्रव्यमान के कणों के द्वि-कण निकाय पर विचार कीजिए। यदि प्रथम कण को द्रव्यमान केंद्र की ओर d दुरी तक धकेला जाता है, तो द्रव्यमान केंद्र को समान स्थिति पर रखते हुए द्वितीय कण को कितनी दुरी तक गति करनी चाहिए :
View Solutionएक खिलाडी 20 m/s की दर से गतिमान 150 g द्रव्यमान की एक क्रिकेट गेंद को पकड़ता है। यदि गेंद पूर्ण रूप से पकड़ने में लगा समय 0.1 s है तो खिलाडी के हाथों पर गेंद द्वारा लगाया गया बल है -
View Solution0.50 kg द्रव्यमान का एक ब्लॉक एक चिकनी सतह `2.00 ms^(-1)` पर चाल से गतिशील है। यह 1.00 kg के दूसरे द्रव्यमान से टकराता है फिर वे एकसाथ एक रकल पिंड के रूप में गति करते है। टक्कर के दौरान ऊर्जा में कमी है :
View SolutionL लम्बाई की एक पतली छड़ x- अक्ष के अनुदिश रखी हुई है जिसके सिरे x = 0 व x = L पर है। इसका रेखीय घनत्व (द्रव्यमान/लम्बाई) `k ((x)/(L))^(n)` के अनुसार x के साथ परिवर्तित होता है, जहाँ n शून्य या कोई धनात्मक संख्या हो सकती है। यदि छड़ के द्रव्यमान केंद्र की स्थिति `x_(CM), n` के विरुद्ध निरूपित की जाती है, निम्न में से कौनसा आरेख n पर `x_(CM)` की निर्भरता को लगभग सही प्रकार से दर्शाता है ?
View Solutionएक क्षैतिज प्रत्यास्थ प्लेट पर h = 4.9 m ऊँचाई से गिरती हुई एक रबर गेंद पर विचार कीजिए। मानाकि टक्कर की अवधि नगण्य है तथा प्लेट के साथ टक्कर पूर्णतया प्रत्यास्थ है। तब समय के फलन के रूप में वेग एवं समय के फलन के रूप में ऊँचाई होगी-
View Solutionकथन-1 : समान दिशा में गतिशील दो कण पूर्णतया अप्रत्यास्थ टक्कर में अपनी ऊर्जा का ह्यास कर देता है।
कथन-2 : संवेग के संरक्ष्ण का सिद्धांत सभी प्रकार की टक्करों के लिए सत्य होता है।
View Solutionनिम्न चित्र 0.4 kg द्रव्यमान की एक वस्तु की एकविमीय गति का स्थिति-समय (x-t) आरेख दर्शाता है। प्रत्येक आवेग का परिणाम है :-
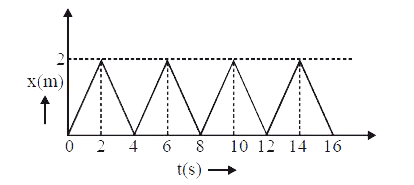
View Solutionप्रकथन -I : चाल v से गतिशील द्रव्यमान m का एक बिंदु कण स्थिर द्रव्यमान M के एक बिंदु कण के संघट्ट करता है। यद सम्भव अधिकतम ऊर्जा क्षय दिया जाता है `f((1)/(2)mv^(2))` से, तब `f = ((m)/(M+m))`.
प्रकथन-II : अधिकतम ऊर्जा क्षय तभी होता है जब संघट्ट के परिणामस्वरूप कण एक दूसरे चिपक जाते हैं।
View Solutionएक ठोस एकसमान शंकु के शीर्ष से इसके द्रव्यमान केंद्र की दुरी `z_(0)` है। यदि इसके आधार की त्रिज्या एवं इसकी ऊँचाई h है तो `z_(0)` का मान है :
View Solution2v चाल से x दिशा में गतिशील m द्रव्यमान के एक कण V से चाल से Y दिशा में गतिशील 2M द्रव्यमान वाल दूसरा कण टकराता है। यदि टक्कर है। यदि टक्कर पूर्णतया अप्रत्यास्थ है, तो टक्कर के दौरान ऊर्जा में प्रतिशत कमी लगभग है :
View Solutionद्रव्यमान M एवं प्रांरभिक वेग V के एक कण A की टक्कर द्रव्यमान `(m)/(2)` के स्थिर कण B से होती है। यह टक्कर सम्मुख एवं प्रत्यास्थ है। टक्कर के बाद डि-ब्रॉगली तरंगदैर्ध्यों `lambda_(A)` से `lambda_(B)` का अनुपात होगा।
View Solutionयदि एक न्यूट्रॉन की एक स्थिर अवस्था के ड्यूटीरियम से प्रत्यास्थ एक रेखीय संघट्ट होती है तो उसकी ऊर्जा का आंशिक क्षय `p_(d)` पाया जाता है। उसके स्थिर अवस्था के कार्बन नाभिक से समरूप संघट्ट में ऊर्जा का आंशिक क्षय पाया जाता है। `p_(d)` तथा `p_(c)` के मान क्रमशः होंगे :
View Solutionएक एकरेखीय संघट्ट (collinear collision ) में, आरम्भिक चाल `v_(0)` का एक कण समान द्रव्यमान के एक दूसरे रुके हुए कण से टकराता है। यदि कुल अंतिम गतिज ऊर्जा , आरम्भिक गतिज ऊर्जा `50%` ज्यादा हो तो टक्कर के बाद दोनों कणों के सापेक्ष गति का प्रणाम होगा :
View Solution
Exercise -3 (JEE Main Previous Year.s Questions) questions and complete solutions for chapter MOMENTUM AND COLLISION of BANSAL PHYSICS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 PHYSICS MOMENTUM AND COLLISION
- Exercise - 4 (JEE ADVANCED Previous Year.s Questions)
- Exercise - 5 (Potential Problems Based on CBSE)
- Exercise -1 (Objective Questions) Reasoning Type
- Exercise -1 (Objective Questions) Matrix Type
- Exercise -1 (Objective Questions) Multiple Correct Choice Type
- Exercise -1 (Objective Questions) Paragraph Type
- Exercise -1 (Objective Questions) Single Correct Choice Type
- Exercise -2 (Subjective Questions)
- Exercise -3 (JEE Main Previous Year.s Questions)
- ILLUSTRATION