Complete Solutions to EXERCISE- 1 (Objective Questions) [SINGLE CORRECT CHOICE TYPE] of chapter FLUID MECHANICS & ELASTICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FLUID MECHANICS & ELASTICITY |
| BANSAL HINDI | EXERCISE- 1 (Objective Questions) [SINGLE CORRECT CHOICE TYPE] |
| Number Of Questions | 88 |
| Academic Year | 2023-24 |
एक खुला घनाकार टैंक प्रारम्भ में पानी से पूरा भरा हुआ है। जब टैंक को क्षैतिज दिशा में त्वरित किया जाता है तो पानी का 1/3 भाग बाहर फैल जाता है तो त्वरण होगा।
View Solutionदो पतली उर्ध्वाधर कांच की नलियां द्रव्य से भरी हुई एक केशिका से जुड़ी है। बाई नली बर्फ में `0^(@)C` पर है तथा दाई नली `30^(@)C` पर पानी में है दोनों नलियों में द्रव्य के स्तर में 4 cm का अन्तर है। नली पर `0^(@)C` में द्रव्य की लम्बाई 120 cm है। आयतन प्रसार गुणांक द्रव्य के लिये क्या होगा। (कॉच का प्रसार नगण्य मानो)

View Solutionचित्र में दर्शायी गई मोटी नली का अनुप्रस्थ काट का क्षेत्रफल 800 `cm^(2)` है। द्रव्यमान रहित पिस्टन पर एक 12 kg का द्रव्यमान रखा है। दोनों नलियों में पानी की सतह की ऊँचाईयों में अंतर होगा।

View SolutionR त्रिज्या का बेलनाकार पात्र में कुछ द्रव भरा है माना कि बेलन के पेंदे में द्रव द्वारा लगाया गया बल `F_(1)` है। अब इस द्रव को एक समान वर्गाकार अनुप्रस्थ काट क्षेत्रफल तथा R भुजा वाले पात्र में डाल दिया जाये तो पात्र के पेदें में द्रव द्वारा लगाया गया बल `F_(2)` हो जाता है, तो (वायुमण्डलीय दाब को नगण्य मानिये) –
View Solutionदोनों सिरों पर खुली, एक समान अनुप्रस्थ काट क्षेत्रफल वाली U-नली में प्रत्येक भुजा में पेंदे से 20 cm ऊँचाई तक पानी भरा है। किसी एक भुजा में 4 gm/cc वाला द्रव डाल दिया जाता है। जिससे तल 5cm और उपर उठ जाता है। अब दोनों नलियों में द्रवों के तल की ऊँचाईयों का अनुपात `h_(2)//h_(1)` होगा।

View Solutionपानी की टंकी के फंदे पर दाब 3P है जहाँ P वायुमण्डलीय दाब है। यदि इस टेंक से 1/5 भाग पानी निकाल लिया जाये तो टैंक के पेंदे पर दाब क्या होगा।
View Solutionएक U– नली जिसकी क्षैतिज भुजा 20 cm तथा जिसका अनुप्रस्थ काट क्षेत्रफल 1`cm^(2)` है। इस नली में 60 cc जल भरा हुआ है। 4g/cc वाले द्रव का कितना आयतन U– नली की एक भुजा में डाला जाये ताकि U नली की क्षैतिज भुजा में जल ना बचें ?
View Solutionएक बाल्टी में 15 cm ऊँचाई तक पानी भरा है। बाल्टी एक रस्सी से बंधी है जो एक घर्षण रहित हल्की घिरनी से गुजरती है। रस्सी का दुसरा सिरा एक ब्लॉक से बंधा है। जिसका द्रव्यमान, (बाल्टी + पानी ) के द्रव्यमान का आधा है। पेंदे पर पानी का दाब वायुमण्डलीय दाब से कितना अधिक होगा।
View Solutionएक घनाकार बंद पात्र जिसकी लम्बाई L है एक गाड़ी में रखा गया है जो 'a' त्वरण से क्षैतिज दिषा में गतिषील है। पात्र एक आदर्ष द्रव से भरा है जिसका घनत्व `rho` है। घनाकार पात्र के केन्द्र पर गैज दाब (gauge pressure) है।

View Solutionएक हल्का अर्ध बेलनाकार गेट जिसकी त्रिज्या R है, मध्य बिन्दु O पर टिका है। तथा इसने `rho` घनत्व वाले द्रव को चित्र के अनुसार रोक रखा है। तो बल F जो गेट को घुमने से रोकेगा

View Solutionअत्यधिक पृष्ठीय क्षेत्रफल वाले एक पात्र में `rho` घनत्व वाला द्रव भरा जाता है। इस पात्र में एक घनाकार टुकड़ा जिसकी भुजा a तथा द्रव्यमान M है, तैर रहा है तथा इसका 4/5 भाग द्रव में डुबा है। एक m द्रव्यमान का एक सिक्का सावधनी से इस टुकड़े के उपर रखा जाता है। तक ब्लॉक ठीक डूबा रहता है, तो M का मान क्या होगा।
View Solutionएक लड़के के एक हाथ में एक मछली तथा दूसरे हाथ में एक बाल्टी है। बाल्टी में पानी भरा है। यदि वह मछली को पानी में डाल देता है तो यह मानते हुए कि पानी नही फैलता है, लड़के द्वारा ढोया जाने वाला भार होगा।
View Solution0.5`gcm^(-3)` घनत्व वाला कार्क का टुकड़ा तरण ताल में तैर रहा है। कार्क के आयतन का कितना भाग पानी में होगा।
View Solution2m की ऊँचाई से एक 0.8 आपेक्षिक घनत्व वाली गेंद को पानी में गिराया जाता है। गेंद पानी में किस गहराई तक प्रवेश करेगी।
View Solution`rho` घनत्व वाली एक लकड़ी की गेंद को `sigma` घनत्व वाले पानी में h गहराई तक डुबोया जाता है और छोड़ दिया जाता है पानी की सतह से कितना ऊपर तक यह जा सकती है।
View Solutionएक गोला जिसका व्यास 7 cm एवं द्रव्यमान 266.5 gm द्रव में तैर रहा है। यदि तापमान बढ़ा दिया जाता है तो गोला `35^(@)C` पर डूबने लगता है। यदि `0^(@)C` पर घनत्व 1.527 gm/cc है तो द्रव का आयतन प्रसार गुणांक बताओं।
View Solutionद्रव में डूबने पर किसी ठोस के वजन में ह्यस `W_(0)` तापमान `0^(@)C` पर एवं W तापमान `t^(@)C` पर है । यदि आयतनिक प्रसार ठोस के `gamma_(s)` व द्रव के लिए `gamma_(1)` है तो W का मान होगा।
View Solutionएक धातु से बना पतला बेलनाकार बर्तन जिसका रेखीय प्रसार गुणांक `10^(-3)""^(@)C^(-1)` है इसमें बेंजीन भरा है। जिसका आयतनिक प्रसार गुणांक `10^(-3)""^(@)C^(-1)` है। यदि बर्तन तथा बेंजीन को `10^(@)C` गर्म किया जाता है, तो तल पर बेंजीन के द्वारा लगाया गया दाब है।
View Solutionएक ठोस गोला पूरी तरह से द्रव्य में डूबा हुआ है। यदि आयतनिक प्रसार गुणांक गोले एवं द्रव्य के लिये `3xx10^(-6)` एवं `8xx10^(-6)` प्रति `""^(@)C` क्रमशः है। यदि तापमान 100 °C बढ़ा दिया जाता है तो प्लव बल में कितने प्रतिशत का परिवर्तन होगा।
View SolutionM द्रव्यमान वाला एक खोखला गोला जिसकी त्रिज्या R है, को जल (`rho_(w)` घनत्व) में डुबोया जाता है। गोला जल में तैर सकता है यदि मुक्त हो तो, यह गोला पैंदे पर दो तारों द्वारा जो एक दूसरे से `45^(@)` के कोण पर है टिका हुआ है। तार के तनाव `T_(1)` क्या होगा।

View Solutionदो समरूप बेलनों के पैंदे में a त्रिज्या का एक छिद्र `(a lt lt R)` है। छिद्र पर R त्रिज्या की एक गेंद रखी जाती है तथा बेलन में जल ऐसे भरा जाता है कि पैंदे से कोई जल बाहर न निकले । स्थिति-1 में जल h ऊँचाई तक भरा जाता है तथा द्वितीय स्थिति में यह 2h ऊँचाई तक भरा जाता है। यदि स्थिति-1 में गोले पर द्रव द्वारा कुल बल `F_(1)` है तथा स्थिति-2 में गोले पर द्रव द्वारा कुल बल `F_(2)` है, तो

View SolutionR त्रिज्या तथा `sigma` आपेक्षिक घनत्व वाला एक गोला में एक r त्रिज्या की संकेन्द्रिय गुहा है। इसे पानी से भरे एक टेंक में रखे जाने पर ठीक तैरता है। तो `R//r` का अनुपात ज्ञात करों।
View SolutionV आयतन, `rho` घनत्व वाली एक वस्तु पात्र के पेंदे से रस्सी द्वारा जुड़ी है पात्र में भरे द्रव का घनत्व d है तथा `d(gt rho)` दिया हुआ है। पात्र उपर की ओर a त्वरण से गतिशील है। रस्सी में तनाव होगा।

View Solutionसोनोमीटर तार की आवृति f है, लेकिन तनाव उत्पन्न करने वाले भार को पानी में पूर्णतया डुबाने पर आवृति f/2 हो जाती है और भार को किसी ओर द्रव में पूर्णतया डुबाने पर आवृति f/3 हो जाती है तो द्रव का सापेक्षक घनत्व क्या है।
View Solutionएक बेलनाकार ब्लॉक जिसका अनुप्रस्थ काट का क्षेत्रफल A तथा घनत्व `rho` है के `1//3` घनत्व वाले द्रव में रखा जाता है ब्लॉक स्प्रिंग को अपनी लम्बाई के `1//3` भाग तक संकुचित कर देता है। यदि गुरूत्वीय त्वरण g है तो स्प्रिंग का स्प्रिंग नियतांक होगा।

View Solutionएक बीकर जिसमें पानी भरा है, एक स्प्रिंग तुला के उपर रखा है। तुला का माप 1.5 kg है। एक पत्थर 0.5 kg एवं घनत्व 500 kg/`m^(3)` को पानी में पूर्णतया डुबा दिया गया है, लेकिन बीकर को स्पर्श नही करता। तो तुला का नया माप क्या होगा ?
View Solutionदो एक समान लम्बाई L तथा एक समान अनुप्रस्थ काट क्षेत्रफल वाले दो बैलन जो `d_(1)` तथा `d_(2)` घनत्व वाले पदार्थ से बने है। दोनों को जोड़कर एक 2L लम्बाई का बेलन बनाकर d घनत्व वाले द्रव में रखने पर इसका L/2 भाग द्रव के उपर रहता है। यदि `d_(1) gt d_(2)` हो तो -
View Solutionसाधारण तुला की दो भुजाओं से V तथा 2V आयतन की दो वस्तुओं को लटकाया जाता है। और दोनों संतुलित स्थिति में रहती है। यदि बड़ी वस्तु (`d_(1)=0.9gm//cm^(3)` घनत्व) वाले तेल में डुबी है और छोटी वस्तु एक अज्ञात द्रव में डुबी है एवं तुला संतुलित है तो अज्ञात द्रव का घनत्व क्या होगा।
View Solutionएक समान 2L लम्बाई की एक बेलनाकार छड़ जो आंशिक रूप से पानी में डुबी हुई है। चित्रानुसार इसके एक सिरे को रस्सी से बंधा गया है । यदि छड़ का विशिष्ट गुरूत्व 0.75 है तो छड़ की कितनी लम्बाई पानी से ऊपर होगी।
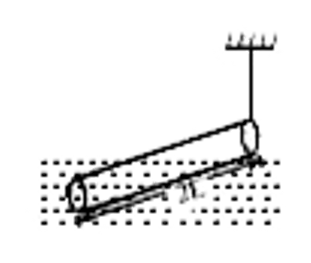
View Solutionडम्ब–बेल (dumbbell) को `rho` घनत्व वाले जल में रखा गया है। छड़ से m द्रव्यमान का एक कण जोड़ने पर यह पाया गया है कि डम्ब–बेल क्षैतिज रूप से पानी की सतह पर तैरता है। और प्रत्येक गोला आधा पानी में डूबा रहता है। m द्रव्यमान का आयतन नगण्य मानते हुए `l` का मान ज्ञात करो।

View Solutionदो घन जिनमें प्रत्येक की भुजा 1.0 m है तथा जिनका आपेक्षिक घनत्व क्रमशः 0.60 तथा 1.15 है, को एक भारहीन तार द्वारा जोडकर पानी के टैंक में रख दिया जाता है। साम्यावस्था में हल्का घन पानी की सतह से कितनी ऊँचाई पर होगा।
View Solutionएक घनाभाकार लकड़ी का टुकड़ा जिसकी भुजाएँ क्रमशः a, b तथा c है तथा जिसका आपेक्षिक घनत्व d है। यह बड़े पानी के टैंक में इस प्रकार तैर रहा है कि इसकी भुजा a उर्ध्वाधर हो जाती है। यदि इसे थोड़ा नीचे विस्थापित करके छोड़ दिया जाता है तो इसका आवर्तकाल ज्ञात करो।
View Solutionएक R त्रिज्या तथा H ऊँचाई का एक शंकु `rho` घनत्व वाली द्रव के एक रस्सी द्वारा लटका हुआ है। द्रव के कारण शंकु की निचली सतह पर बल होगा। (वायुमण्डलीय दाब को नगण्य माने)

View SolutionR त्रिज्या के एक बेलन की तली से R त्रिज्या का ही अर्द्धगोलाकार भाग अलग कर दिया जाता है। शेष बचे बेलनाकार भाग का आयतन V तथा द्रव्यमान M है। इस भाग को एक डोरी द्वारा उर्ध्वाधर `rho` घनत्व वाले द्रव में लटका दिया जाता है। बेलन का ऊपरी सिरा द्रव के पृष्ठ से h गहराई पर है। द्रव द्वारा बेलन के निचले सिरे पर आरोपित बल है।

View Solutionएक धात्विक टुकड़ा जो बर्फ के टुकड़े में है यह पानी की सतह पर तैर रहा है। बर्फ पिघलने पर धात्विक टुकड़ा पानी में गिर जाता है। पात्र में पानी का स्तर -

View Solutiona = 20 cm आकार का एक बर्फ का घन जल से भरी एक झील में तैर रहा है। बर्फ का आपेक्षिक घनत्व 0.9 है। बर्फ के पूर्णतः पिघल जाने पर गुरूत्वीय स्थितिज ऊर्जा में परिवर्तन होगा -
View Solutionएक लकड़ी का ब्लॉक जिस पर एक सिक्का रखा है चित्रानुसार पानी पर तैरता है। दूरियाँ `l` तथा h चित्रानुसार है। कुछ समय बाद सिक्का पानी में गिर जाता है, तब

View Solutionबाग में पाये जाने वाले फव्वारे में अक्सर यह देखा जाता है कि इसके एक सिर पर एक मोटा पाइप दूसरे सिरे पर कही छोटे छिद्र होते है। इसी प्रकार के फव्वारे में पाइप की आंतरिक व्यास 2 cm तथा पानी के बहने की दर 3 `ms^(-1)` है। प्रत्येक छोटे छिद्र का व्यास 0.05 cm है तथा छिद्रो की संख्या 100 है तो छिद्र से बाहर निकलने वाले पानी का वेग m/s में ज्ञात करों।
View Solutionदो पाइप P तथा Q जिनका व्यास `2xx10^(-2)` तथा `4xx10^(-2)m` है को श्रेणी क्रम में जोड़कर पानी की मुख्य लाइन से जोड़ा गया है। पाइप P में बहते हुए पानी का वेग होगा
View Solutionबर्नोली प्रमेय किसके संरक्षण के सिद्धान्त को प्रदर्शित करती है।
View Solutionएक आदर्श द्रव के लिये निम्न में से कौनसी अभिधारणा बरनोली प्रमेय लगाने के लिये सही नहीं है -
View Solutionएक असमान अनुप्रस्थ काट क्षेत्रफल वाली नली से क्षैतिज दिशा में पानी बह रहा है। यदि 0.02 `m^(2)` अनुप्रस्थ काट क्षेत्रफल वाले बिन्दु पर दाब `4 xx10^(4)N//m^(2)` तथा द्रव का वेग 2 m/s है तो उस बिन्दु पर दाब क्या होगा जहां अनुप्रस्थ काट का क्षेत्रफल 0.01`m^(2)` है
View Solutionपानी का एक बैरल जमीन से h ऊँचाई पर टेबल पर रखा है। यदि बैरल के पार्श्व दीवार पर पेंदे से सटे हुए एक छेद कर दिया जाए तो निकला हुआ पानी R क्षैतिज दूरी पर जमीन से टकराता है। बैरल की गहराई है।
View Solutionएक बड़ा टेंक (घनत्व `=10^(3)kg//m^(3)`) वाले पानी से भरा है। ऊपर से 10 m नीचे एक छिद्र है। छिद्र से निकलने वाला पानी पृथ्वी सतह पर R दूरी पर जाकर गिरता है। पानी की सतह पर अतिरिक्त दाब क्या है ताकि पानी पृथ्वी सतह पर 2R दूरी पर जाकर गिरे। (दिया है `1 atm =10^(5)Pa` तथा `g = 10 m//s^(2)`):

View Solution1000 `cm^(2)` अनुप्रस्थ काट क्षेत्रफल का एक बेलनाकार पात्र में 10 kg का एक घर्षण रहित पिस्टन लगा है। पात्र पानी से भरा हुआ है। पिस्टन से 50 cm दूरी पर 10 `mm^(2)` से. का एक छोटा छिद्र बनाया जाता है। छिद्र से निकलते हुए पानी का वेग है।
View Solution`rho` तथा `2rho` घनत्व के दो अमिश्रय (immicible) तरल पात्र में चित्रानुसार भरे है। हल्के द्रव के सतह से क्रमशः `h//2` तथा `3h//2` दूरी पर दो छेद किए गए है। यदि छेदों से निकलते हुए द्रव का वेग क्रमशः `v_(1)` तथा `v_(2)` हो तो `v_(1)//v_(2)` है।

View Solutionएक बड़ा H ऊँचाई का टेंक पूरा पानी से भरा है। टेंक के पेंदे में एक छोटा छिद्र कर दिया जाता है। यह `eta` गुना पानी का स्तर कम करने में `T_(1)` समय लगाता है जहाँ `(eta gt 1)` है तथा पूर्ण पानी को खाली करने में `T_(2)` समय लगाता है। यदि `T_(1)=T_(2)` है तो `eta` का मान होगा।
View Solutionशराब से भरा घनाकार बाक्स में पैंदे के एक सिरे पर एक छोटा छिद्र है। जब बॉक्स शराब से पूरा भर कर क्षैतिज सतह पर रखा जाता है तो छिद्र से निकलने वाले द्रव का प्रारम्भिक वेग `v_(0)` है। जब बॉक्स आधा खाली हो जाता है तो उसे चित्रानुसार ऐसे `45^(@)` घुमा दिया जाता है कि छिद्र निम्नतम बिन्दु पर हो, तब छिद्र से निकलने वाले द्रव का वेग होगा। (मानाकि ऊपरी वायु वायुमण्डलीय दाब पर है)

View Solutionपानी से भरे एक बंद पात्र से एक नली चित्रानुसार जुड़ी है। छोटे छिद्र से निकलने वाले पानी को वेग होगा।

View Solution`6cm^(2)` वाले छिद्र से पानी का फुव्वारा निकलकर दिवार के अभिलम्ब से `60^(@)` के कोण पर टकराता है तथा यह टक्कर प्रत्यास्थ होती है। यदि फव्वारे का वेग 12 m/s से हो तो दीवार पर लगने वाला बल होगा।
View Solutionएक अग्निशमन यंत्र से निकलने वाले पानी का घनत्व `rho` तथा पानी के निकलने की आयतन की दर L है। पाइप में से पानी पहले उर्ध्वाधर उपर जाता है फिर `90^(@)` पर मुड़कर क्षैतिज रूप से V वेग से बाहर आता है। सभी स्थानों पर पाइप का अनुप्रस्थ काट का क्षेत्रफल समरूप है तो पाइप से गुजरने वाले जल द्वारा मोड़ पर लगाये गये बल का मान होगा।

View Solutionएक उर्ध्वाधर टेंक जो उपर से खुला है, एक द्रव से भरा है और चिकनी क्षैतिज सतह पर रखा है। टेंक के एक तरफ केन्द्र पर 1 छिद्रकर दिया जाता है टेंक का अनुप्रस्थ काट का क्षेत्रफल छिद्र के अनुप्रस्थ काट क्षेत्रफल का N गुना है। टेंक का द्रव्यमान नगण्य है टेंक का प्रारम्भिक त्वरण क्या होगा।
View Solutionएक बेलनाकार पात्र में H ऊँचाई तक पानी भरा जाता है। पात्र की पार्वी दिवार पैदें दो स्पर्श करता हुआ एक वृताकार छिद्र है। पात्र के पेंदे तथा तल के मध्य घर्षण गुणांक `mu` है पात्र तथा पानी का कुल द्रव्यमान M है। छिद्र का न्यूनतम व्यास क्या होना चाहिये कि पात्र फर्श पर गति करना प्रारम्भ कर दें। (यदि प्लग को हटा दिया जाये, मान लिजिए पानी का घनत्व `rho` है।)
View Solutionपानी से भरे एक पात्र के पेंदे में एक 0.1 mm व्यास का वृताकार छिद्र है। बिना लीक किये पात्र में कितनी ऊँचाई तक पानी को भरा जा सकता है ?
पृष्ठ तनाव `=75xx10^(-3)N//m` तथा `g=10m//s^(2)`:
View Solutionयदि दो अलग-अलग त्रिज्याओं के साबुन के बुलबुले एक दूसरे से एक नली द्वारा जुड़े है तो -
View Solutionएक लम्बी 'r' त्रिज्या की केशिकीय नली प्रारम्भ में उर्ध्वाधर है और `0^(0)` स्पर्श कोण वाले द्रव में पूरी डुबी है। यदि नली को थोड़ा ऊपर उठाया जाये तब नली का विस्थापन तथा चन्द्रतल की वक्रता त्रिज्या के बीच ग्राफ है।
View Solutionआन्तरिक त्रिज्या r = 0.25 mm की एक काँच की केशनली जल में डूबोई जाती है। नली का शीर्ष सिरा जल सतह से 2 cm ऊपर रहता है। द्रव, नली से किस कोण पर मिलता है? जल का पृष्ठ तनाव `=0.07Nm^(-1)` तथा इसका स्पर्श कोण `0^(@)` है।
View Solutionएक द्रव की प्रत्येक त्रिज्या की कुछ गोल बूंदे सम्मिलित होकर R त्रिज्या की एक एकल बूंद का निर्माण करती है। यदि T पृष्ठ तनाव है, तो मुक्त ऊर्जा होगी -
View SolutionR त्रिज्या का एक साबुन का बुलबुला दर्शाये अनुसार 2R त्रिज्या के दूसरे साबुन के बुलबुले से घिरा हुआ है। पृष्ठ तनाव = S लिजिये तो, छोटे साबुन के बुलबुले के भीतर वायुमण्डलीय दाब से दाबाधिक्य होगा -

View Solutionअल्प पृथकता दूरी 'd' पर रखी दो विशाल समान्तर काँच प्लेटें `rho` घनत्व व S पृष्ठ तनाव वाले एक द्रव में डूबोयी जाती हैं। द्रव के बाहरी स्तर के सापेक्ष प्लेटों के बीच द्रव स्तर की ऊँचाई ज्ञात कीजिये। द्रव-काँच अन्तरापृष्ठ के लिये स्पर्श कोण `theta` है।
View Solution`pi` ग्राम द्रव्यमान, 2mm त्रिज्या व नगण्य मोटाई की एक लम्बी केशनली को 0.1 N/m पृष्ठ तनाव के एक द्रव में आंशिक रूप से डूबोया जाता है। स्पर्श कोण को शून्य लें व उत्प्लावन बल को नगण्य मानें। नली को ऊर्ध्वाधरतः बनाये रखने के लिये आवश्यक बल होगा – `(g=10m//s^(2))`

View Solutionएक खुली केशनली को पारे से भरे एक पात्र में डूबोया जाता है। पात्र में व केशनली में पारे के स्तरों के बीच का अन्तर `Deltah=4.6mm` है। केशनली में पारे के नवचन्द्रक की वक्रता त्रिज्या क्या है ? पारे का पृष्ठ तनाव 0.46 N/m है, पारे का घनत्व 13.6 gm/cc है।
View Solution1 cm त्रिज्या की एक नली के मुँह पर एक साबुन का बुलबुला फलाया जा रहा है। साबुन के घोल का पृष्ठ तनाव 0.05 N/m है तथा बुलबुला दर्शाये अनुसार नली से `60^(@)` का कोण बनाता है। नली में वायुमण्डलीय दाब पर दाबाधिक्य है :

View Solutionr त्रिज्या की एक पतली धात्विक वलय जल सतह पर तैरती है तथा परिधि के नीचे की सतह वलय के ऊर्ध्व किनारे से `theta` कोण बनाते हुये मुड़ जाती है। यदि वलय W भार का जल विस्थापित करती है तथा जल का पृष्ठ तनाव T है, तो धात्विक वलय का भार है -
View Solution1 mm त्रिज्या की एक काँच छड़ 2 mm की भीतरी त्रिज्या वाली एक काँच की केशनली में सममित रूप से प्रवेश करायी जाती है। फिर सम्पूर्ण उपकरण को जल की सतह के सम्पर्क में लाया जाता है। जल का पृष्ठ तनाव `7xx 10^(-2)` N/m है। जल केशनली में किस ऊँचाई तक चढ़ेगा? `(theta=0^(@))`
View Solutionएक बड़ी फिक्स पट्टिका तथा 100 `cm^(2)` अनुप्रस्थ काट क्षेत्रफल वाली एक समतल पट्टिका के मध्य 1mm मोटी ग्लिसरीन की परत है। यदि ग्लिसरीन का श्यानता गुणांक 1.0 kg/m-s है तो पट्टिका को 7 cm/s के वेग से हटाने के लिये लगाया गया बल होगा ?
View Solutionएक घनाकार गुटका जिसमें प्रत्येक भुजा 'a' तथा घनत्व '`rho`' है। एक आनत तल पर चित्रानुसार 'v' वेग से खिसक रहा है। एक 't' मोटाई की पतली फिल्म आनत तल तथा गुटका के बीच है तो पतली फिल्म का श्यानता गुणांक होगा।

View Solutionएक साफ्ट तथा स्लीव के बीच का क्षेत्र न्यूटोनियन तरल से भरा है। जब साफ्ट पर स्लीव के समानान्तर 800N बल लगाया जाता है तो यह 1.5 cm/sec का वेग प्राप्त कर लेता है। 2.4 kN बल लगाने साफ्ट को वेग होगा।
View Solutionएक ठोस r त्रिज्या का धात्विक गोला मुक्त रूप से हवा में गिरता है। यदि हवा का घर्षण बल अनुप्रस्थ काट क्षेत्रफल के समानुपाती तथा वस्तु के वेग के वर्ग समानुपाती है तो गोले का सीमांत वेग निम्न में से होगा ?
View Solutionदो समान त्रिज्या की बूंदे स्थिर वेग v cm/s से हवा में गिर रही है। यदि दोनों बूंदे आपस में मिल जाये तो सीमांत वेग होगा ?
View Solutionइनमें से कौन वर्षा की बूंदो की गति को सर्वोतम प्रदर्शित करता है ?
View Solutionएक श्यान द्रव में गिरते हुए गोले का निम्न में से कौनसा ग्राफ I gh ugh है ?
(दिया गया t= 0, पर v = 0 तथा विस्थापन x = 0.)
View Solutionश्यान माध्यम में मुक्त रूप से गिरती वस्तु का विस्थापन समय ग्राफ दिया है। निम्न में से कौनसा ग्राफ सही होगा -
View Solutionएक भारी खोखला R त्रिज्या तथा h ऊँचाई का शंकु जिसका आधार क्षैतिज सतह पर रखा है। इस शंकु को `rho` घनत्व वाले पानी से पूर्ण रूप से भर दिया जाता है। शंकु के आधार पर वृताकार परिधि सील पैक है तथा शंकु के शीर्ष पर एक छोटा छिद्र है। पानी द्वारा शंकु पर ऊपर की ओर लगाया जाने वाला बल होगा। (वायुमण्डलीय दाब को नगण्य मानिये)
View Solutionक्षैतिज नली का अनुप्रस्थ काट का क्षेत्रफल द्रव के बहाव की दिशा में लम्बाई के अनुदिश बढ़ता है। तो लम्बाई के अनुदिश बहाव की दिशा x में दाब परिवर्तन होगा।
View Solutionपृथ्वी सतह से h ऊँचाई तक एक R त्रिज्या वाले गोले में पानी भरा है। इस स्थिति में द्रव की सतह किनारों पर क्षैतिज रहती है। स्पर्श कोण होगा।

View Solutionबेलनाकार तार के आयतन एवं त्रिज्या का परिवर्तन क्रमशः 0.2% एवं 0.002% है, जब उस पर पर्याप्त बल लगाया जाता है। तो तार का अनुदैर्ध्य प्रतिबल क्या होगा।
`(Y=2.0xx10^(11)Nm^(-2))`
View Solutionएक बेलनाकार बर्तन जिसमें द्रव भरा है तथा उसके उपर भार रहित पिस्टन लगा है। इस द्रव में प्रत्यास्थता गुणांक K तथा त्रिज्या R का गोला रखा है। जब पिस्टन पर द्रव्यमान m रखा जाता है तो गोले की त्रिज्या का आंशिक परिवर्तन `delta//R` बताओं।
View Solutionएक बेलनाकार तार जिसकी त्रिज्या 1 mm, लम्बाई 1 m, प्रत्यास्थता गुणांक `=2xx10^(11)N//m^(2)` पॉयसन अनुपात `mu=pi//10`, उस पर 100 N का बल लगाकर खिंच रहा है। उसकी त्रिज्या क्या होगी।
View Solutionएक समान छड़ गुरूत्वाकर्षण मुक्त क्षेत्र में नियत कोणिय वेग से घूम रही है। छड़ में तन्य प्रतिबल के घुमाने की दूरी x से परिवर्तन किस प्रकार होगा।
View Solutionचार समान धातुओं से बने तारो का बल लगने पर विक्रति का लेखाचित्र दिखाया गया है। निम्न में से कौनसा लेखाचित्र सबसे मोटे तार का है।

View Solutionअपने एक सिरे से ऊर्ध्वाधर लटका हुआ एक तार निचले सिरे पर 200 N के भार को जोड़ कर खींचा जाता है। भार तार को 1 mm विस्तारित कर देता है, तो तार में संचित प्रत्यास्थ ऊर्जा है -
View Solutionआप तार के टुकड़े के गुणों का परीक्षण करने के लिये एक बहुत विशेष प्रयोग करते हैं। आप तार के प्रत्येक सिरे पर बाहर की ओर बल लगाकर तार को खींचते हैं तथा इसकी लम्बाई में परिवर्तन का मापन करते हैं। यदि अब आप इस बल को ठीक दुगुना कर देते हैं तथा तार अब भी प्रत्यास्थ बना रहता है लेकिन आनुपातिक सीमा से बाहर होता है, तो तार की लम्बाई में परिवर्तनः
View SolutionM अल्प द्रव्यमान व L भुजा एक उच्च दृढ़ घनाकार ब्लॉक A समान विमाओं व निम्न दृढ़ता गुणांक n पर दृढ़ता से इस प्रकार लगा हुआ है कि A का निचला फलक B के ऊपरी फलक को पूर्णतया ढक लेता है। B का निचला फलक एक क्षैतिज सतह पर दृढ़ता से रखा हुआ है। एक लघु बल F,A के किसी एक पार्श्व फलक के लम्बवत् शीर्ष पर आरोपित किया जाता है। B की दीवार `phi` कोण से घूम जाती है। अब सम्पूर्ण उपकरण को पलटकर उल्टा रख दिया जाता है जिससे A का निचला फलक दृढ़ता से क्षैतिज सतह पर रखा होता है तथा हम B के फलक के लम्बवत् शीर्ष पर एक अल्प बल F लगाते हैं। अब B की दीवार किस कोण से घूम जाती है?
View Solutionकॉपर का प्रत्यास्थता गुणांक `1.4xx10^(11)` पासकल एवं तापीय प्रसार गुणांक `1.7xx10^(-5)(C^(@))^(-1)` है तो कितना दाब लगाने पर कॉपर गुटके को बढ़ने से रोका जा सकता है। जब उसका तापमान `20^(@)C` से `30^(@)C` तक बढ़ा दिया जाये?
View Solutionएक वर्गाकार अनुप्रस्थ काट की छड़ जिसकी लम्बाई 1 cm है। इस छड़ को गर्म करने पर इसका तापमान `t^(@)C` बढ़ जाता है। तो कितना संपीड़न बल लगाकर छड़ को बढ़ने से रोका जा सकता है। (E -यंग प्रत्यास्थता गुणांक) (`alpha` तापीय प्रसार गुणांक)
View Solutionएक धातु से बना पतला बेलनाकार बर्तन जिसका रेखीय प्रसार गुणांक `10^(-3)""^(@)C^(-1)` है इसमें बेंजीन भरा है। जिसका आयतनिक प्रसार गुणांक `10^(-3)""^(@)C^(-1)` है। यदि बर्तन तथा बेंजीन को `10^(@)C` गर्म किया जाता है, तो तल पर बेंजीन के द्वारा लगाया गया दाब है।
View Solutionएक समरूप दाब P एक ठोस घन की सभी भुजाओं पर लगाया जाता है। इसका आयतन दाब लगाने से पूर्व के आयतन तक वापस लाने के लिये इसे `Deltat^(@)` से गर्म किया जाता है, तो :
View Solution
EXERCISE- 1 (Objective Questions) [SINGLE CORRECT CHOICE TYPE] questions and complete solutions for chapter FLUID MECHANICS & ELASTICITY of BANSAL PHYSICS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 PHYSICS FLUID MECHANICS & ELASTICITY
- EXERCISE - 3 (JEE Main Previous Year.s Questions)
- EXERCISE- 1 (Objective Questions) [MULTIPLE CORRECT CHOICE TYPE]
- EXERCISE- 1 (Objective Questions) [PARAGRAPH TYPE]
- EXERCISE- 1 (Objective Questions) [REASONING TYPE]
- EXERCISE- 1 (Objective Questions) [SINGLE CORRECT CHOICE TYPE]
- EXERCISE-2 (Subjective Questions)
- EXERCISE-4 (JEE ADVANCED Previous Year.s Questions)
- EXERCISE-5 (Potential Problems Based on CBSE)
- Illustration