Complete Solutions to EXERCISE-4 SECTION-A (JEE ADVANCED Previous Year) of chapter ज्यामितीय प्रकाशिकी of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ज्यामितीय प्रकाशिकी |
| BANSAL HINDI | EXERCISE-4 SECTION-A (JEE ADVANCED Previous Year) |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
प्रदर्शित समउत्तल लैंस का फोकस दूरी 15 cm है। लैंस के समतल पृष्ठ को चांदी से लेपित किया गया है लैंस के मुख्य अक्ष पर एक बिम्ब 20 cm की दूरी पर रखा जाता है। बिम्ब का प्रतिबिम्ब बनेगा।
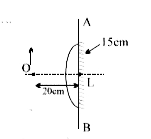
View Solutionयदि सूर्य के समान्तर किरणों f फोकस दूरी वाले उभयोतल लैन्स से अपवर्तन के बाद वृताकार प्रतिबिम्ब फोकस तल पर 1 त्रिज्या का बनता है तो निम्न में सही कथन है ?
View Solutionजल में चलने वाली एक प्रकाश-किरण जल के पृष्ट पर, तो वायु में खुला हैं, आपतित होती है। तब:
View Solutionकथन-1 : गोलीय दर्पण के लिये u. v तथा f के बीच सम्बन्ध स्थापित करने वाला सूत्र सिर्फ उन दर्पणों के लिये सही है जिनके आकार उनकी वक्रता त्रिज्याओं की तुलना में बहुत छोटे होते है।
कारण 1 : प्रकाश के परावर्तन के नियम समतल दर्पण के लिये पूरी तरह सही है पर बड़े आकार की गोलीय सतहों के लिये नहीं।
View Solutionलाल तथा बैंगनी प्रकाश के दो पुंज एक प्रिज्म (प्रिज्म `60^(@))` से अलग-अलग गुजरते है। न्यूनतम विचलन की स्थिति में अपवर्तन कोण होगा।
View Solutionनीचे प्रदर्शित चित्र में, एक प्रकाश पुंज क्षेत्र I से क्षेत्रा IV तक यात्रा कर रहा है। क्षेत्र I. II, III तथा IV के अपवर्तनांक क्रमश `n_(0),(n_(0))/(2),(n_(0))/(6)` तथा `(n_(0))/(8)` है। यह आपतन कोण `theta` जिसके लिये पुंज क्षेत्र (IV) में प्रवेश न करे अर्थात थोड़ा सा चूक जाये -

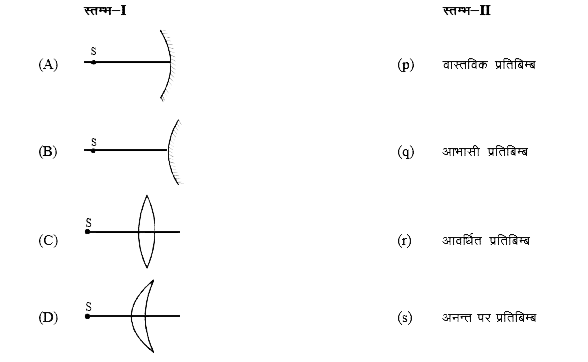
View Solutionएक प्रकाशीय घटक व एक वस्तु स्तम्भ-I में दी गई इसकी प्रकाशीय अक्ष के अनुदिश स्थित है। वस्तु तथा घटक के मध्य दूरी बदल सकती है। प्रतिबिम्ब की प्रकृति स्तम्भ II से प्रतिबिम्ब के सभी गुणो को स्तम्भ-I में दिये गये उचित घटको से मिलान कीजिये ।
View Solutionएक झील के जल की सतह से 20 मीटर की ऊंचाई पर एक गेंद छोड़ी जाती है। जल का अपवर्तनांक `4//3` है। झील में स्थित एक मछली, जो गेंद के गिरने की रेखा में है, गिरती हुई गेंद को देख रही है। जब गेंद जल की सतह से `12.8` मीटर ऊपर है उस समय मछली गेंद की गति को देखेगी: (g=10 `मीटर/सेकंड^(2)`)
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View Solutionएकवर्णी प्रकाश की एक किरण OP , एक प्रिज़्म ABCD के फ़लक AB पर शीर्ष B के निकट `60^(@)` के अनुपात कोण पर आपतित होती है [चित्र VI. 26]। यदि प्रिज़्म के पदार्थ का अपवर्तनांक `sqrt(3)` हो , तो इनमें से क्या सही है (हैं ) ?
View Solutionएक पतले उभयोत्तल लेंस की फोकस दूरी 20 सेमी है | जब लेंस के सामने बिम्ब को 25 सेमी से 50 सेमी दूर ले जाया जाता है तो इसके प्रतिबिम्ब का आवर्धन `m_(25)` से `n_(50)` हो जाता है | `(m_(25))/(m_(50))` अनुपात का मान क्या होगा ?
View Solutionएक उपभयोतल लेंस जिसकी फोकस दूरी 15cm है एक समतल दर्पण के सामने 10cm पर रखा है। एक वस्तु को यदि लेंस से 30 cm की दूरी पर रखें तो अंतिम प्रतिबिम्ब होगा
View Solutionएक वस्तु जो कि 20 m वक्रता कि त्रिज्या वाले उत्तल दर्पण के प्रकाशिक अक्ष पर चल रही है का प्रतिबिम्ब `(25)/(3)m` से `(50)/(7)m` पर 30 सेकण्ड में चली जाती है। तो वस्तु का किमी प्रति घंटे में गति क्या होगी?
View Solutionएक बड़ी शीशे की प्लेट `(mu = 5//3)` जिसकी मोटाई 8 cm है एक प्रकाश के बिन्दुवत स्रोत पर रखा है। प्लेट के उपर R त्रिज्या के वृताकार क्षेत्र से रोशनी आती है दिख रही है R का मान कितना होगा ?
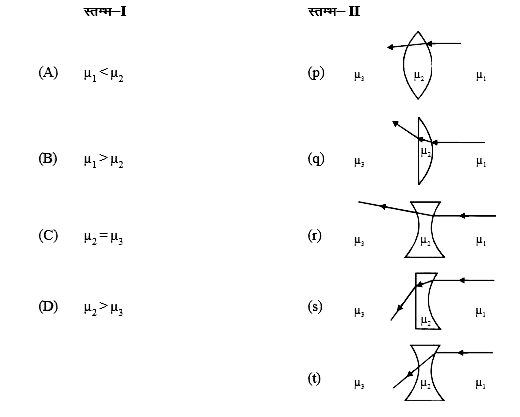
View Solution`mu_(1)` और `mu_(2)` अपवर्तनांक वाले दो पारदर्शक माध्यम के बीच एक `mu_(2)` अपवर्तनांक का लेंस चित्रानुसार रखा है। इन माध्यमों से गुजरने वाली प्रकाश की किरण भी चित्र में दर्शायी गयी है। स्तम्भ-I में अपवर्तनांक में सम्बन्ध और स्तम्भ-II में रेखा चित्र दिया है। इन्हें मिलाये।
View Solutionएक प्रकाश किरण कॉच में चलकर कॉच-वायु अंतरापृष्ठ पर आपतन कोण से पड़ रही है। परावर्तित (R) एवं निर्गमित (T) तीव्रताओं में बदलाव कोण के सदृश खींचे गये है। सही ग्राफ है
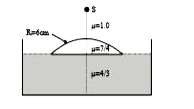
View Solutionएक टैंक में 18 cm गहरा पानी (अपवर्तनांक `(4)/(3)` है। पानी पर अपवर्तनांक `(7)/(4)` का तेल पड़ा है जिसकी सतह उत्तल है व 'R = 6 cm' त्रिज्या की है (चित्र देखिये) तेल को पतले लैंस की तरह मानिये। एक बिम्ब 'S' पानी की सतह से 24 cm ऊपर है। प्रतिबिम्ब टैंक के तल से 'x' cm ऊपर है। तब 'x' का मान है-
View Solutionचित्र में दर्शाये अनुशार, दो पतले समतल-उत्तल लेन्सों को मिलाकर एक उभयोत्तल लेन्स बना है | पहले लेन्स का अपवर्तनांक (n) 1.5 तथा दूसरे का 1.2 है | दोनों लेन्सों के गोलीय फलको की वक्रता-त्रिज्या R = 14 सेमी है | उभयोत्तल लेन्स के लिये यदि वस्तु की दूरी 40 सेमी हो, तब प्रतिबिम्ब की दूरी होगी :

View Solutionअधिकतर पदार्थो का अपवर्तनांक, `n gt 1` होता है। इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम, `(sin theta_(1))/(sin theta_(2))=(n_(2))/(n_(1))`के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है। लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती। विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक `n=((c)/(v))=+- sqrt(epsi_(r)mu_(r))`, होता है, जहाँ C विद्युत – चुम्बकीय तरंगों की निर्यात में चाल तथा v उनकी माध्यम में चाल हैं, `epsi_(r)` व `mu_(r)` क्रमशः माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं। आम पदार्थों में `epsi_(r)` व `mu_(r)` दोनों धनात्मक होते हैं, अर्थात माध्यम का n धनात्मक है। जब `epsi_(r)` व `mu_(r)` दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा। ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-metarial) कहते हैं। वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते। चूँकि n ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है। तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती।
सही प्रकथन चुनें।
View Solutionअधिकतर पदार्थो का अपवर्तनांक, `n gt 1` होता है। इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम, `(sin theta_(1))/(sin theta_(2))=(n_(2))/(n_(1))`के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है। लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती। विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक `n=((c)/(v))=+- sqrt(epsi_(r)mu_(r))`, होता है, जहाँ C विद्युत – चुम्बकीय तरंगों की निर्यात में चाल तथा v उनकी माध्यम में चाल हैं, `epsi_(r)` व `mu_(r)` क्रमशः माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं। आम पदार्थों में `epsi_(r)` व `mu_(r)` दोनों धनात्मक होते हैं, अर्थात माध्यम का n धनात्मक है। जब `epsi_(r)` व `mu_(r)` दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा। ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-metarial) कहते हैं। वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते। चूँकि n ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है। तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती।
वायु (air) से मैटा-पदार्थ पर आपतित प्रकाश-किरण के लिये उपयुक्त किरण-चित्र है
View Solutionएक समतल-उत्तल लेंस एक वास्तविक प्रतिबिंब लेंस के 8m पीछे बनाता है जो कि वस्तु के आकार का एक-तिहाई है। लेंस के अन्दर प्रकाश की तरंगदैर्ध्य निर्वात की तरंगदैर्ध्य से `(2)/(3)` गुना है। लैंस के वक्रित पृष्ठ की त्रिज्या है
View Solutionएक समतल दर्पण पर आपतित प्रकाश किरण की प्रगामी दिशा `(1)/(2)(hati+sqrt3hatj)` है | परावर्तन के बाद प्रगामी दिशा `(1)/(2)(hati-sqrt3hatj)` हो जाती है | किरण का आपतन कोण है
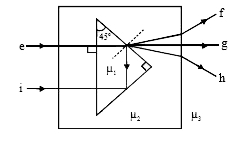
View Solution`mu_(1)` अपर्तनांक के एक समकोण प्रिज्म को `mu_(2)` अपवर्तनांक के आयताकार ब्लाक में रखा गया है। पूर्ण व्यवस्था `mu_(3)` अपवर्तनांक के माध्यम से चित्र में दर्शाए अनुसार घिरी हुई है। प्रकाश की किरण 'e' आयताकार ब्लॉक पर अभिलंबवत् आपतित की जाती है। `mu_(1), mu_(2)` और `mu_(3)` के मानों पर निर्भर प्रकाश की किरण चार संभव पथों 'ef, 'eg'. 'eh' या 'ei' में से एक लेती है।
सूची I में दिये गये पथों को सूची II की अपवर्तनांक की शर्तो से सुमेलित कीजिए और सूचियों के नीचे दिये कोड का प्रयोग करके सही उत्तर चुनिये-
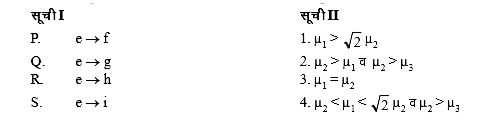
View Solutionकाँच के एक लम्बे व ठोस बेलन, जिसका अपवर्तनांक `n_(2)=1.5` है, का एक छोर गोलीय जैसा कि चित्र में दर्शाया गया है | इस गोलीय पृष्ठ की त्रिज्या rR है और इस पर `n_(1)=1.4` अपवर्तनांक की एकसमान मोटाई वाली एक पारदर्शी पतली फ़िल्म लगी है | वायु से फ़िल्म में होकर काँच में जाने वाली प्रकाश की किरणें जो कि बेलन के अक्ष के समान्तर हैं, फ़िल्म से `f_(1)` दूरी पर फोकसित होती हैं, जबकि काँच से वायु में जाने वाली किरणें फ़िल्म से `f_(2)` दूरी पर फोकस होती हैं, तब

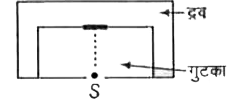
View Solutionएक बिंदु प्रकाश स्रोत (S) एक 10 मिमी ऊँचाई वाले पारदर्शी गुटके की निचली सतह पर रखा गया है | गुटके का अपवर्तनांक 2.72 है | गुटके को एक कम अपवर्तनांक वाले द्रव में डुबोया जाता है, जैसा चित्र में दर्शाया गया है | गुटके से निकलकर द्रव में जाने वाला प्रकाश, गुटके की ऊपरी सतह पर 11.54 मिमी व्यास का एक दीप्त वृत्त बनाता है | द्रव का अपवर्तनांक है
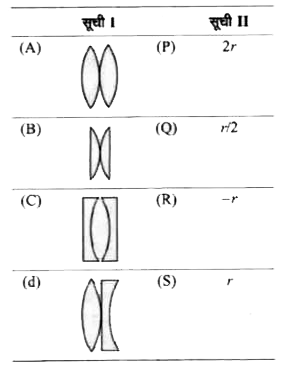
View Solutionदो पतले लेंसों के चार संयोजन सूची I में दिए गए हैं | प्रत्येक लेंस के वक्रीय पृष्ठ की वक्रता त्रिज्या r तथा अपवर्तनांक 1.5 है | सूची I में विभिन्न लेंस संयोजन दिए गए हैं तथा सूची II में उनकी फोकस दूरी दी हुई है | सूची I को सूची II से सुमेलित कीजिए तथा सूचियों के नीचे दिए गए कोड का प्रयोग करके सही उत्तर चुनिए
View Solutionएक अवतल दर्पण तथा उत्तल लेंस (अपवर्तनांक = 1.5) जिनमें प्रत्येक की फोकस दूरी 10 cm है, दर्शाये चित्रानुसार एक दूसरे से 50 cm की दूरी पर वायू (अपवर्तनांक = 1) में स्थित हैं। एक वस्तु को दर्पण से 15 cm की दूरी पर रखा गया है। इस संयोजन द्वारा वस्तु के सीधे बनने वाले प्रतिबिंब का आवर्धन `M_(1)` है। जब यह सेट-अप 7/6 अपवर्तनांक के माध्यम में रखा जाता है तब आवर्धन `M_(2)` हो जाता है। `|(M_(2))/(M_(1))|` के परिमाण का मान है-

View Solutionदो समरूप काँच की छड़े `S_(1)` तथा `S_(2)` (अपवर्तनांक = 1.5 ) जिनके एक छोर उत्तल है | जिनकी वक्रता त्रिज्या 10 सेमी है | इनके वक्र पृष्ठ एक दूसरे से d दूरी पर दर्शाये चित्रानुसार रखें है तथा उनकी अक्षे एक रेखा (बिन्दुदार रेखा द्वारा दिखायी गई ) पर है | यदि प्रकाश के एक बिन्दु स्त्रोत P को छड़ `S_(1)` कि भीतर वक्र पृष्ठ से 50 सेमी की दूरी पर रखने पर इससे निकलने वाली प्रकाश की किरणे छड़ `S_(2)` कि भीतर अक्ष के समांतर हो, तब दूरी d होगी :

View Solutionप्रकाश-विद्युत प्रभाव में आपतित फोटॉन की तरंगदैर्ध्य `lambda` है तथा निरोधी विभव `V_(0)` है। `V_(0)` का `lambda` तथा `(1)/(lambda)` के साथ सही ग्राफ है (है)
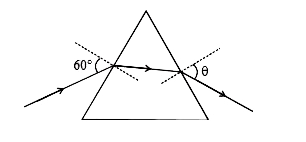
View Solutionएकवर्णी प्रकाश का एक पुंज एक n अपवर्तनांक वाले समबाहु प्रिज्म के एक फलक पर `60^(@)` के कोण पर आपतित होता है तथा सामने वाले फलक से लम्ब से (n) कोण बनाते हुए निकलता है (चित्र देखें)| `n=sqrt(3)` पर `theta` का मान `60^(@)` है तथा `(d theta)/(dn)=m` है। तब m का मान है :
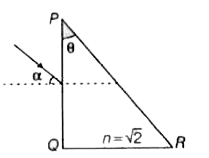
View Solutionवायु से आती प्रकाश की एक समान्तर किरण पुँज एक समकोण त्रिभुजीय प्रिज्म, जिसका अपवर्तनांक `n= sqrt2` है, के PQ तल पर `alpha` कोण से आपतित होती है | जब `alpha` का न्यूनतम मान `45^(@)` है, तो प्रकाश का प्रिज्म की पर सतह पर पूर्ण आतंरिक परावर्तन होता है | प्रिज्म का कोण 0 क्या होगा ?
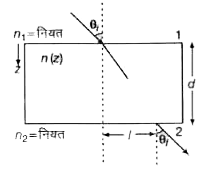
View Solutiond मोटाई के एक पारदर्शी पट्ट के अपवर्तनांक n(z) का मान z बढ़ाने से बढ़ता है | यहाँ z पट्ट के अंदर ऊपरी सतह से मापी गयी ऊर्ध्वाधर दूरी है | पट्ट को दो `n_(2)(gt n_(1))` माध्यमों के बीच रखा गया है जिनके एकसमान अपवर्तनांक `n_(1)` एवं `n_(2)(gtn_(1))` है, जैसा कि चित्र में दर्शाया गया है | यहाँ `n_(1)` और `n_(2)` स्थिर हैं | प्रकाश की एक किरण माध्यम 1 से पट्ट पर, `theta_(i)` कोण से आपतित है तथा माध्यम 2 में पाश्विक विस्थापन l से अपवर्तन कोण, `theta_(f)` पर निकसित होती है |
View Solutionएक समतल - उत्तल लेंस के पदार्थ का अपवर्तनांक n है | जब एक छोटी वस्तु को लेंस के वक्रपृष्ठ के सामने 30 सेमी की दूरी पर रखते हैं, तो उस वस्तु के दोगुने आकार का प्रतिबिम्ब बनता है | उत्तल पृष्ठ से परावर्तन के कारण लेंस से 10 सेमी की दूरी पर एक क्षीण प्रतिबिम्ब भी बनता है | निम्नलिखित में से कौन - सा/कौन - से कथन सत्य है/हैं ?
View Solutionएक छोटी वस्तु को 30 सेमी फोकस दुरी वाले एक पतले उत्तल लेन्स की बायीं ओर 50 सेमी की दूरी पर रखा गया है | 100 सेमी की वक्रता त्रिज्या वाले एक उत्तल गोलाकार दर्पण को लेन्स के दायीं ओर 50 सेमी की दूरी पर रखा गया है | दर्पण को इस प्रकार से झुकाया गया है कि दर्पण की अक्ष लेन्स की अक्ष से `theta = 30^(@)` का कोण बनती है, जैसा चित्र में दर्शाया गया है
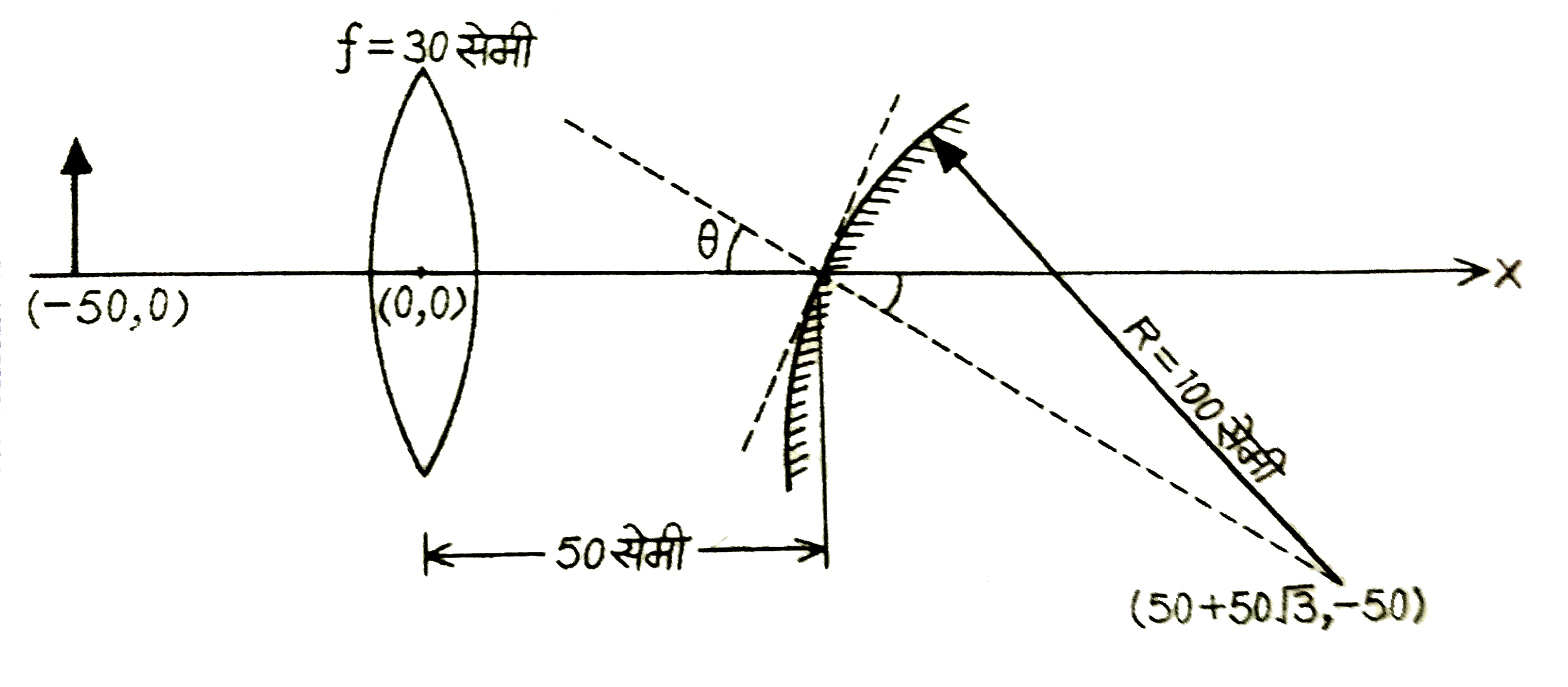
यदि निर्देशांक पद्धति का मूल बिंदु लेन्स के मध्य में हो, तो जहाँ प्रतिबिम्ब बना है उस बिंदु का निर्देशांक (x,y) सेमी में है :
View Solutionएक समद्विबाहु प्रिज्म कोण A है (isosceles prism of angleA)। इस प्रिज्म का अपवर्तनांक है। इस प्रिज्म का न्यूनतम विचलन कोण (angle of minimum deviation) =`delta_(m)=A` है। निम्न में से कौन सा (से) कथन सही है/हैं?
View Solutionएकवर्णी प्रकाश (monochromatic light) अपवर्तनांक n = 1.6 वाले माध्यम में प्रगामी है। यह प्रकाश काँच की चीती (stack of glass layers) पर निचले सतह से `theta=30^(@)` कोण पर आपतित होता है (जैसा कि चित्र में दर्शाया गया है) काँचों के स्तर परस्पर समांतर है। काँच के चीती के अपवर्तनांक एकदिष्ट`n_(m)=n-mDeltan` क्रम से घट रहे हैं। यहाँ `m^(th)` स्तर का अपवर्तनांक `n_(m)` और `Deltan=0.1` है। प्रकाश किरण `(m-1)^(th)`एवं m स्तर के पृष्ठतल से समांतर दिशा में दाईओर के बाहर निकलता है। तब m का मान होता है ?
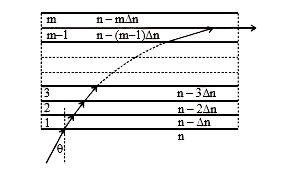
View Solutionसूर्य का प्रकाश , जिसकी तीव्रता `1.3kW-m^(-2)` है, एक पतले उत्तल लेन्स पर अभिलम्बवत तरीके से आपतित होता है। लेन्स की फोकस दुरी `20cm` है। लेन्स द्वारा होने वाली प्रकाश की ऊर्जा के क्षय की उपेक्षा कीजिए और मान लीजिए की लेन्स का द्वारक माप उसकी फोकस दुरी से बहुत कम है। लेन्स के दूसरी तरफ की दुरी `22cm` प्रकाश की औसत तीव्रता .......... `kWm^(-2)` है।
View Solutionएक तार को एक समकोण त्रिभुज के आकार में मोड़ कर fफोकस दूरी (focal length) वाले एक अवतल दर्पण (concave mirror) के सामने रखा गया है, जैसा कि चित्र में दर्शाया गया है। चार विकल्प चित्रों में से कौनसा (से) चित्र मुड़े हुये तार के प्रतिबिम्ब का सही आकार गुणात्मक तरीके से दर्शाता है (दर्शाते है)? (ये चित्र स्केल के अनुसार नहीं है)
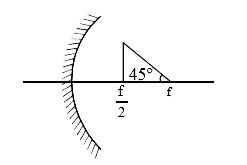
View Solution
EXERCISE-4 SECTION-A (JEE ADVANCED Previous Year) questions and complete solutions for chapter ज्यामितीय प्रकाशिकी of BANSAL PHYSICS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 PHYSICS ज्यामितीय प्रकाशिकी
- EXERCISE-1 (Objective Questions) [SINGLE CORRECT CHOICE TYPE]
- EXERCISE-1 ([PARAGRAPH TYPE] Paragraph for question)
- EXERCISE-1 [MULTIPLE CORRECT CHOICE TYPE]
- EXERCISE-1 [REASONING TYPE]
- EXERCISE-2 (Subjective Questions)
- EXERCISE-3 (JEE Main Previous Year)
- EXERCISE-4 SECTION-A (JEE ADVANCED Previous Year)
- EXERCISE-5 (CBSE Previous Year.s Questions)