Complete Solutions to EXERCISE - 4 (JEE ADVANCED Previous Year.s Questions) of chapter आधुनिक भौतिकी of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | आधुनिक भौतिकी |
| BANSAL HINDI | EXERCISE - 4 (JEE ADVANCED Previous Year.s Questions) |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
प्रकाश वैद्युत प्रभाव के एक प्रयोग में तीन धातुओं (जिनके कार्य फलन `phi_1, phi_2 " तथा "phi_3` है) के लिए `1//lambda` तथा निरोधी विभय (V) के बीच ग्राफ खींचे गये चित्रानुसार है। कौन-सा/से कथन सही है/है? [`lambda`आपतित विकिरण की तरंगदैर्ध्य है]
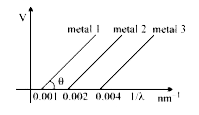
View Solutionलाइमन श्रेणी की nवीं रेखा की तरंगदैर्ध्य, हाइड्रोजन-सदृश तत्व (z=11) की निम्नतम ऊर्जा स्तर में स्थित इलेक्ट्रॉन की डी-ब्रोग्ली तरंगदैर्ध्य के बराबर है , n का मान ज्ञात कीजिए? [दिया है: बोहर त्रिज्या `(r_0) = 0.53 Å` तथा रिडबर्ग नियतांक `(R ) =1.1 xx 10^7 m^(-1)`]
View Solutionरेडियम-226 के नमूने की अर्द्धआयु 4 दिन है। 2 अर्द्धआयु में एक नाभिक के क्षय होने की प्रायिकता होगी।
View Solutionनिम्नलिखित कॉलम का मिलान कीजिये।
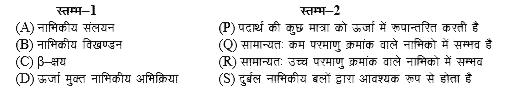
View Solutionहाइड्रोजन स्पेक्ट्राम के पराबैंगनी क्षेत्र में दीर्घतम तरंगदैर्ध्य 122 mm होती है। इस स्पेक्ट्रम के अवरक्त क्षेत्र में लघुत्तम तरंगदैर्ध्य है। (निकटतम पूर्णक में)
View Solutionकथन-1: यदि एक x-किरण नलिका में त्वरण विभव (accelerating potential ) को बढ़ा दिया जाता है तो अभिलाक्षणिक X-किरणों की तरंगदैर्ध्य नहीं बदलती ।
कथन-2: जब एक इलेक्ट्रॉन पुंज X-किरण नलिका में लक्ष्य पर पड़ता है तो गतिज ऊर्जा का एक भाग X-किरणों की ऊर्जा में बदल जाता है।
View SolutionX-किरण नलिका में डी-बोग्ली तरंगदैर्ध्य `lambda` के इलेक्ट्रॉन लक्ष्य पर गिरते हैं। उत्सर्जित X- किरणों की संस्तब्ध तरंगदैर्ध्य है
View Solutionनीचे दिये गये विकल्पों में E एक नाभिक की स्थिर द्रव्यमान ऊर्जा तथा एक न्यूट्रॉन को निरूपित करता है। सही विकल्प है:
View Solution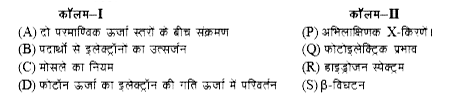
View SolutionX-किरण नलिका में X-किरणों के उत्सर्जन से संबन्धित, निम्न में से कौनसा कथन गलत है?
View Solution`H - He^(+)` गैसों के मिश्रण (`He^(+)` एक आयनित हीलियम परमाणु है) में H परमाणु तथा `He^(+)` एक आयनित हीलियम परमाणु है) में H परमाणु तथा `He^(+)` आयनों को स्थानान्तरित कर देते है। यह माना गया है कि बोहर परमाणु मॉडल पूर्णतया वैध है।
अन्तिम अवस्था में प्राप्त `He^(+)` आयनों के लिए मुख्य क्वाण्टम संख्या n है
View Solution`H - He^(+)` गैसों के मिश्रण (`He^(+)` एक आयनित हीलियम परमाणु है ) में H परमाणु तथा `He^(+)` एक आयनित हीलियम परमाणु है जो कि प्रथम उत्तेजित अवस्था में है ) ) में H परमाणु तथा `He^(+)` आयनों को स्थानान्तरित कर देते है। यह माना गया है कि बोहर परमाणु मॉडल पूर्णतया वैध है।
`He^(+)` आयनों की H-परमाणु से टक्कर के बाद दृश्य प्रकाश क्षेत्र में उत्सर्जित प्रकाश की तरंगदैर्ध्य है
View Solution`H - He^(+)` गैसों के मिश्रण (`He^(+)` एक आयनित हीलियम परमाणु है) में H परमाणु तथा `He^(+)` एक आयनित हीलियम परमाणु है) में H परमाणु तथा `He^(+)` आयनों को स्थानान्तरित कर देते है। यह माना गया है कि बोहर परमाणु मॉडल पूर्णतया वैध है।
H-परमाणु की तथा `He^(+)` आयन की n = 2 इलेक्ट्रॉन के संगत गतिज ऊर्जाओं का अनुपात है
View Solutionमान ले कि नाभिकीय बंधन-ऊर्जा प्रति न्यूक्लियान (B/A) बनाम द्रव्यमान संख्या (A) नीचे दर्शाये चित्र के अनुसार है। इस ग्राफ का उपयोग करते हुये सही उत्तरों का चुनाव करें।
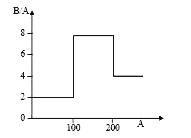
View Solutionएक रेडियोकर्मी नमूना S1 (जिसकी सक्रियता 5uCi है) में नाभिकों की संख्या एक दूसरे रेडियोधर्मी नमूने S2 (जिसकी सक्रियता `10mu Ci` है) से दो गुनी है। S1 तथा S2 की अर्ध-आयु निम्न हो सकती है।
View Solutionजब एक कण को x-अक्ष पर x= 0 तथा x = a, जहाँ नैनोमीटर के आस-पास है, चलने के लिए सीमित किया जाता है। तब इस कण की ऊर्जा के कुछ विशेष मान ही हो सकते है। इस सीमित क्षेत्र में गति करते कण की संभव ऊर्जाएँ इस क्षेत्र में बनने वाली अप्रगामी तरंगों से सम्बन्धित है, जिनके लिए x=0 तथा x = a पर निस्पन्द बन रहे हों। इन अप्रगामी तरंगों का तरंगदैर्ध्य, इस कण का रेखीय संवेग से डी-ब्रोगनी समीकरण के अनुसार सम्बन्धित है। द्रव्यमान m के कण की ऊर्जा एवं इसके रेखीय संवेग के बीच सम्बन्ध है, `E = p^2/(2m)`| अतः कण की ऊर्जा को एक क्वांटम संख्या 'n' जिसके मान 1,2,3, ... (n = 1, को मूल अवस्था कहते है) हो सकते हैं, के द्वारा दर्शाया जा सकता है। इस संख्या का सम्बन्ध अप्रगामी तरंगों में बन रहे लूपों की संख्या से है।
उपरोक्त मॉडल की सहायता से निम्नलिखित तीन प्रश्न हल करें। जब कण x=30 से x = तक रेखा पर चल रहा है।
` h = 6.6 xx 10^(-34) Js " तथा " e = 1.6 xx 10^(-19) C`
n के किसी एक मान के लिए कण की संभव ऊर्जा समानुपाती है
View Solutionजब एक कण को x-अक्ष पर x= 0 तथा x = a, जहाँ नैनोमीटर के आस-पास है, चलने के लिए सीमित किया जाता है। तब इस कण की ऊर्जा के कुछ विशेष मान ही हो सकते है। इस सीमित क्षेत्र में गति करते कण की संभव ऊर्जाएँ इस क्षेत्र में बनने वाली अप्रगामी तरंगों से सम्बन्धित है, जिनके लिए x=0 तथा x = a पर निस्पन्द बन रहे हों। इन अप्रगामी तरंगों का तरंगदैर्ध्य, इस कण का रेखीय संवेग से डी-ब्रोगनी समीकरण के अनुसार सम्बन्धित है। द्रव्यमान m के कण की ऊर्जा एवं इसके रेखीय संवेग के बीच सम्बन्ध है, `E = p^2/(2m)`| अतः कण की ऊर्जा को एक क्वांटम संख्या 'n' जिसके मान 1,2,3, ... (n = 1, को मूल अवस्था कहते है) हो सकते हैं, के द्वारा दर्शाया जा सकता है। इस संख्या का सम्बन्ध अप्रगामी तरंगों में बन रहे लूपों की संख्या से है।
उपरोक्त मॉडल की सहायता से निम्नलिखित तीन प्रश्न हल करें। जब कण x=30 से x = तक रेखा पर चल रहा है।
` h = 6.6 xx 10^(-34) Js " तथा " e = 1.6 xx 10^(-19) C`
यदि कण का द्रव्यमान `m=1.0xx10^(-30)kg` तथा a=6.6 nm, हो, तब मूल अवस्था में कण की ऊर्जा सबसे निकट है :
View Solutionजब एक कण को x-अक्ष पर x= 0 तथा x = a, जहाँ नैनोमीटर के आस-पास है, चलने के लिए सीमित किया जाता है। तब इस कण की ऊर्जा के कुछ विशेष मान ही हो सकते है। इस सीमित क्षेत्र में गति करते कण की संभव ऊर्जाएँ इस क्षेत्र में बनने वाली अप्रगामी तरंगों से सम्बन्धित है, जिनके लिए x=0 तथा x = a पर निस्पन्द बन रहे हों। इन अप्रगामी तरंगों का तरंगदैर्ध्य, इस कण का रेखीय संवेग से डी-ब्रोगनी समीकरण के अनुसार सम्बन्धित है। द्रव्यमान m के कण की ऊर्जा एवं इसके रेखीय संवेग के बीच सम्बन्ध है, `E = p^2/(2m)`| अतः कण की ऊर्जा को एक क्वांटम संख्या 'n' जिसके मान 1,2,3, ... (n = 1, को मूल अवस्था कहते है) हो सकते हैं, के द्वारा दर्शाया जा सकता है। इस संख्या का सम्बन्ध अप्रगामी तरंगों में बन रहे लूपों की संख्या से है।
उपरोक्त मॉडल की सहायता से निम्नलिखित तीन प्रश्न हल करें। जब कण x=30 से x = तक रेखा पर चल रहा है।
` h = 6.6 xx 10^(-34) Js " तथा " e = 1.6 xx 10^(-19) C`
कण की चाल के कुछ पृथक-पृथक मान होंगे, जो समानुपाती है
View Solutionप्रकाश विद्युत प्रभाव के प्रयोग करने में तीन विभन्न धातु प्लेट p, q तथा r का उपयोग किया गया जिसके कार्य फलन क्रमशः `phi_p = 2.0 eV, phi_q = 2.5 eV " तथा " phi_r = 3.0 eV` है। प्रत्येक प्लेट के उपर एक प्रकाश पुन्ज डाला जाता है जिसमें तरंगदैर्ध्य 550 nm,450 nm तथा 350 nm उपस्थित है। जिनकी तिव्रता समान है। प्रयोग में सही I-V ग्राफ होगा [दिया है he = 1240 eV nm]
View Solutionवैज्ञानिक कड़ी मेहनत से नाभिकीय संलयन रिएक्टर विकसित करने में लगे है। भारी हाइड्रोजन नाभिक `""_1^2H`, जिसे पॅट्रॉन कहते है और D से दर्शाते है। संलयन रिएक्टर के लिये संभावना के रूप में प्रयोग किया जा सकता है। D - D अभिक्रिया है: `""_1^2H + ""_1^2H to ""_2^3 He + n+` ऊर्जा, संलयन रिएक्टर के कोर में भारी हाइड्रोजन गैस, ड्यूट्रॉन नाभिको और इलेक्ट्रॉनों में पूर्णतया आयनित हो जाती है। इन `""_1^2H` नाभिको और इलेक्ट्रॉनों के समूह को प्लाज्मा कहते है। रिएक्टर कोर में नाभिकीय संलयन हो सके। सामान्यता, रिएक्टर कोर में तापमान बहुत बहुत अधिक होता है और इस कारण किसी भी पदार्थ की दीवार इस प्लाज्मा को अपने अन्दर परिसीमित रखने में सक्षम नहीं हो पाती है। इसलिये विशेषज्ञ तकनीको का प्रयोग करके इस प्लाज्मा को कुछ समय तक परिसीमित किया जाता है। इससे पहले कि कण कोर से दूर चले जायें। यदि n ड्यूट्रॉनों का घनत्व (संख्या/आयतन) हो तथा `t_0` परिसीमन समय हो, तो `nt_0` को लासन नम्बर (Lawson number) कहते है।
यदि मानक के अनुसार किसी रिएक्टर को सफल करने के लिये लासन नम्बर का मान `5 xx 10^14 s//cm^3` से अधिक होना चाहिये। नीचे दिये गये स्थिरांको का प्रयोग आपके लिये उपयोगी हो सकता है।
वोल्ट्समान नियतांक `k =8.6 xx 10^(-5) eV//K , e^2/(4 pi epsi_0) = 1.44 xx 10^(-9) eVm`.
नाभिकीय संलयन-रिएक्टर कोर में गैस से प्लाज्मा बनने का कारण है-
View Solutionवैज्ञानिक कड़ी मेहनत से नाभिकीय संलयन रिएक्टर विकसित करने में लगे है। भारी हाइड्रोजन नाभिक `""_1^2H`, जिसे पॅट्रॉन कहते है और D से दर्शाते है। संलयन रिएक्टर के लिये संभावना के रूप में प्रयोग किया जा सकता है। D - D अभिक्रिया है: `""_1^2H + ""_1^2H to ""_2^3 He + n+` ऊर्जा, संलयन रिएक्टर के कोर में भारी हाइड्रोजन गैस, ड्यूट्रॉन नाभिको और इलेक्ट्रॉनों में पूर्णतया आयनित हो जाती है। इन `""_1^2H` नाभिको और इलेक्ट्रॉनों के समूह को प्लाज्मा कहते है। रिएक्टर कोर में नाभिकीय संलयन हो सके। सामान्यता, रिएक्टर कोर में तापमान बहुत बहुत अधिक होता है और इस कारण किसी भी पदार्थ की दीवार इस प्लाज्मा को अपने अन्दर परिसीमित रखने में सक्षम नहीं हो पाती है। इसलिये विशेषज्ञ तकनीको का प्रयोग करके इस प्लाज्मा को कुछ समय तक परिसीमित किया जाता है। इससे पहले कि कण कोर से दूर चले जायें। यदि n ड्यूट्रॉनों का घनत्व (संख्या/आयतन) हो तथा `t_0` परिसीमन समय हो, तो `nt_0` को लासन नम्बर (Lawson number) कहते है।
यदि मानक के अनुसार किसी रिएक्टर को सफल करने के लिये लासन नम्बर का मान `5 xx 10^14 s//cm^3` से अधिक होना चाहिये। नीचे दिये गये स्थिरांको का प्रयोग आपके लिये उपयोगी हो सकता है।
वोल्ट्समान नियतांक `k =8.6 xx 10^(-5) eV//K , e^2/(4 pi epsi_0) = 1.44 xx 10^(-9) eVm`.
मान लें संलयन रिएक्टर कोर में, जिसका तापमान T है, दो टूट्रॉन एक-दूसरे की ओर बढ़ रहे है, प्रत्येक की गतिज ऊर्जा 1.5 kT है, और उनकी आपसी दूरी इतनी ज्यादा है कि उनके बीच कूलॉम विभव ऊर्जा को नगण्य मान सकते है। कोर में उपस्थिति दूसरे कणों के साथ इन दोनों की किसी प्रकार की आपसी क्रिया को भी नगण्य मान सकते है। ये ड्यूट्रॉन `4 xx 10^(-15)m` की दूरी तक पहुंच पाये इसके लिये आवश्यक न्यूनतम तापमान T होगा। इस प्रकार अन्तराल में।
View Solutionवैज्ञानिक कड़ी मेहनत से नाभिकीय संलयन रिएक्टर विकसित करने में लगे है। भारी हाइड्रोजन नाभिक `""_1^2H`, जिसे पॅट्रॉन कहते है और D से दर्शाते है। संलयन रिएक्टर के लिये संभावना के रूप में प्रयोग किया जा सकता है। D - D अभिक्रिया है: `""_1^2H + ""_1^2H to ""_2^3 He + n+` ऊर्जा, संलयन रिएक्टर के कोर में भारी हाइड्रोजन गैस, ड्यूट्रॉन नाभिको और इलेक्ट्रॉनों में पूर्णतया आयनित हो जाती है। इन `""_1^2H` नाभिको और इलेक्ट्रॉनों के समूह को प्लाज्मा कहते है। रिएक्टर कोर में नाभिकीय संलयन हो सके। सामान्यता, रिएक्टर कोर में तापमान बहुत बहुत अधिक होता है और इस कारण किसी भी पदार्थ की दीवार इस प्लाज्मा को अपने अन्दर परिसीमित रखने में सक्षम नहीं हो पाती है। इसलिये विशेषज्ञ तकनीको का प्रयोग करके इस प्लाज्मा को कुछ समय तक परिसीमित किया जाता है। इससे पहले कि कण कोर से दूर चले जायें। यदि n ड्यूट्रॉनों का घनत्व (संख्या/आयतन) हो तथा `t_0` परिसीमन समय हो, तो `nt_0` को लासन नम्बर (Lawson number) कहते है।
यदि मानक के अनुसार किसी रिएक्टर को सफल करने के लिये लासन नम्बर का मान `5 xx 10^14 s//cm^3` से अधिक होना चाहिये। नीचे दिये गये स्थिरांको का प्रयोग आपके लिये उपयोगी हो सकता है।
वोल्ट्समान नियतांक `k =8.6 xx 10^(-5) eV//K , e^2/(4 pi epsi_0) = 1.44 xx 10^(-9) eVm`.
D - D अभिक्रिया के प्रयोग से बन सकने वाले संलयन रिएक्टर के चार सम्भावित प्रारूपों के लिये की गई गणना के परिणाम नीचे दिये गये है। लासन मानक के अनुसार इन चारों में से कौन सफलता का सबसे सशन्त प्रारूप है?
View Solution
View Solutionएक `alpha`-कण तथा एक प्रोटॉन को विरामावस्था से 100V के विभवान्तर द्वारा त्वरित किया जाता है। इसके बाद इनकी दे-बोग्ली तरंगदैर्ध्य क्रमशः `lambda_(alpha)` तथा `lambda_p` हैं। अनुपात `lambda_p/lambda_(alpha)` का मान के निकटतम पूर्णांक क्या होगा?
View Solutionप्रोटॉन के चारों ओर घूमते इलेक्ट्रॉन के कोणीय संवेग का क्याटीकरण, बोहर के हाइड्रोजन परमाणु स्पेक्ट्राम सिद्धान्त का मुख्य आधार है। हम इस सिद्धान्त को ओर आगे बढ़ाते हुए एक सामान्य घूर्णन गति के लिए उपयोग करते है तथा एक द्विपरमाण्विक अणु को दृढ़ मानते हुए उसकी क्वान्टीकृत घूर्णन ऊर्जा निकालेंगे। इसके लिए बोहर के क्वांटीकृतप्रतिबन्ध वाले नियम का उपयोग किया जायेगा।
एक द्विपरमाण्विक अणु का जड़त्व आघूर्ण I है। बोहर के क्वांटीकृत-प्रतिबन्ध के अनुसार, इसके n - स्तर (n= 0 मान्य नहीं है) की घूर्णन ऊर्जा कितनी होगी?
View Solutionयह पाया गया है कि CO अणु के घूर्णन की निम्नतम अवस्था से घूर्णन की प्रथम उत्तेजित अवस्था तक के लिए उत्तेजन आवृत्ति लगभग `4/pi xx 10^11Hz` है। तब COअणु का जड़त्व-आघूर्ण इसके द्रव्यमान केन्द्र के सापेक्ष लगभग कितना होगा?(लिजिए `h = 2 pi xx 10^(-34)Js`)
View Solutionअणु में C (द्रव्यमान = 12 a.m.u.) तथा O(द्रव्यमान = 16 am.u.), के बीच दूरी लगभग कितनी है?
( जहाँ `1 a.m.u. = 5/3 xx 10^(-27) Kg`)
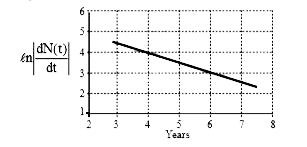
View Solutionरेडियोधर्मी तत्व की अर्द्धआयु ज्ञात करने के लिये एक छात्र `lnabs((dN(t))/(dt))` का t के साथ ग्राफ बनाता है। यहाँ `(dN(t))/(dt)` रेडियोधर्मी क्षय की। समय पर दर है। यदि 4.16 सालों के बाद इस रेडियोधर्मी पदार्थ के नाभिकों की संख्या p घटक से कम हो जाती है. p का मान बताइये।
View Solutionहाइड्रोजन परमाणु की बामर श्रृंखला की पहली स्पेक्ट्रमी लाइन की तरंगदैर्ध्य 6561Å है। तब एकल-आयनित हीलियम परमाणु की बामर श्रृंखला की दूसरी लाइन की तरंगदैर्ध्य होगी।
View Solutionएक ताजा तैयार किये गये रेडियोऐक्टिव नमूने, जिसका माध्य-आयु`10^9 s` है, की एक्टिवविटी `10^10` विघटन प्रति सेकण्ड (disintegrations per second) है। सम्बन्धित रेडियो-आइसोटोप परमाणु का भार `10^(-25)kg` है। ऐडियोएक्टिव नमूने का (mg में) भार है।
View Solutionएक प्रोटॉन को सीधे एक नाभिक `(Q = 120 e`, जहां e इलेक्ट्रॉनिक आवेश है) कि ओर बहुत दूर से दागा जाता है। यह प्रोटॉन नाभिक से 10 fm की निकटतम दूरी तक पहुंचता है । प्रोटॉन के चलना आरम्भ करते समय उसकी de Broglie तरंगदैर्ध्य (fm में) क्या है ? (मानें : प्रोटॉन का द्रव्यमान, `m_p = (5//3) xx 10^(-27) kg, h//e = 4.2 xx 10^(-15) Js//C , 1/(4 pi epsilon_0) = 9 xx 10^(8) m//F , 1 fm = 10^(-15) m)`.
View Solution1900 के आसपास हुई खोज के अनुसार `beta`-क्षय प्रक्रम वास्तव में न्यूट्रॉन (n) का क्षय होता है। प्रयोगशाला में पाया गया है कि न्यूट्रॉन के क्षय होने पर एक प्रोटोन (p) तथा एक इलेक्ट्रॉन (`e^(-)`) जनित होते है। इसलिये, न्यूट्रॉन क्षय को द्वि-पिंडी क्षय-प्रकम मानकर, सैद्धांतिक गणना से यह सिद्ध किया गया कि इलेक्ट्रान की गतिज ऊर्जा का मान स्थिर रहना चाहिये। लेकिन प्रयोगों ने दिखाया कि इलेक्ट्रॉन की गतिज ऊर्जा के मान का संतत स्पेक्ट्रम होता है। त्रि-पिंडी क्षय प्रक्रम मानकर, अर्थात `n to p + e^(-) + vec v_e`, 1930 के आसपास Pauli ने इलेक्ट्रान का देखा गया ऊर्जा स्पेक्ट्रम समझाया। प्रति-न्यूट्रिनों (`vecv_e`) को द्रव्यमान-रहित व नगण्य ऊर्जा का मान कर और न्यूट्रान को स्थिर मान कर, संवेग व ऊर्जा संरक्षण के नियम गणना में लगाये गये जिससे इलेक्ट्रॉन की अधिकतम गतिज ऊर्जा को `0.8 xx 10^6eV` आंका गया। प्रोटान की गतिज ऊर्जा केवल प्रतिक्षेप ऊर्जा है।
प्रति-न्यूट्रिनों की अधिकतम ऊर्जा है।
View Solution1900 के आसपास हुई खोज के अनुसार `beta`-क्षय प्रक्रम वास्तव में न्यूट्रॉन (n) का क्षय होता है। प्रयोगशाला में पाया गया है कि न्यूट्रॉन के क्षय होने पर एक प्रोटोन (p) तथा एक इलेक्ट्रॉन (`e^(-)`) जनित होते है। इसलिये, न्यूट्रॉन क्षय को द्वि-पिंडी क्षय-प्रकम मानकर, सैद्धांतिक गणना से यह सिद्ध किया गया कि इलेक्ट्रान की गतिज ऊर्जा का मान स्थिर रहना चाहिये। लेकिन प्रयोगों ने दिखाया कि इलेक्ट्रॉन की गतिज ऊर्जा के मान का संतत स्पेक्ट्रम होता है। त्रि-पिंडी क्षय प्रक्रम मानकर, अर्थात `n to p + e^(-) + vec v_e`, 1930 के आसपास Pauli ने इलेक्ट्रान का देखा गया ऊर्जा स्पेक्ट्रम समझाया। प्रति-न्यूट्रिनों (`vecv_e`) को द्रव्यमान-रहित व नगण्य ऊर्जा का मान कर और न्यूट्रान को स्थिर मान कर, संवेग व ऊर्जा संरक्षण के नियम गणना में लगाये गये जिससे इलेक्ट्रॉन की अधिकतम गतिज ऊर्जा को `0.8 xx 10^6eV` आंका गया। प्रोटान की गतिज ऊर्जा केवल प्रतिक्षेप ऊर्जा है।
प्रति-न्यूट्रिनों की अधिकतम ऊर्जा है।
View Solutionएक छोटी वस्तु, जो प्रारम्भ में विराम अवस्था में है,प्रकाश 100 ns की एक स्पंद को पूर्णतयाअवशोषित करती है। स्पंद की शक्ति 30 mW है व प्रकाश की चाल ` 3xx 10^8 ms^(-1)` है। वस्तु का अंतिम संवेग है:
View Solutionचांदी एवं सोडियम के कार्य फलन क्रमशः 4.6 व 2.3 eVहै। चांदी व सोडियम के निरोधी विभव एवं आवृति के बीच ग्राफों के ढाल का अनुपात है |
View Solutionएक हाइड्रोजन सदृश परमाणु के इलेक्ट्रॉन कक्ष की त्रिज्या `4.5 a_0` है जहाँ `a_0` बोर त्रिज्या है। इस इलेक्ट्रॉन का क्क्षीय कोणीय संवेग `(3h)/(2pi)` है। दिया है कि h प्लांक नियतांक व R रिडबर्ग नियतांक है। परमाणु के व्युत्तेजित होने पर उत्सर्जित विकिरण के तरगदैर्ध्य की संभावनाएँ हैं
View Solutionएक नाभिक `""_Z^AX` का द्रव्यमान (A-Z) न्यूट्रॉनों एवं Z. प्रोटॉनो के द्रव्यमानों के योग से कम होता है। सम्बन्धित द्रव्यमान अतंर के समतुल्य ऊर्जा को नाभिक की बंधन ऊर्जा कहते है। द्रव्यमान M का एक भारी नाभिक `m_1" एवं "m_2` द्रव्यमानों के दो हल्के नाभिको में विघटित हो सकता है, यदि `(m_1 + m_2)ltM` तथा `m_3 a_4`, द्रव्यमानों के दो हल्के नाभिक पूर्ण संलयन करके, एक M' द्रव्यमान का भारी नाभिक बनाते हैं, यदि `(m_3+m_4)gtM'` | कुछ उदासीन परमाणुओं के द्रव्यमान नीचे टेबल में दिये गये है:

जब विरामावस्था में नाभिक `""_(84)^210Po` ऐल्फा-क्षय करता है, तब ऐल्फा कण की गतिज ऊर्जा (keV में) होती है
View Solutionएक नाभिक `""_Z^AX` का द्रव्यमान (A-Z) न्यूट्रॉनों एवं Z. प्रोटॉनो के द्रव्यमानों के योग से कम होता है। सम्बन्धित द्रव्यमान अतंर के समतुल्य ऊर्जा को नाभिक की बंधन ऊर्जा कहते है। द्रव्यमान M का एक भारी नाभिक `m_1" एवं "m_2` द्रव्यमानों के दो हल्के नाभिको में विघटित हो सकता है, यदि `(m_1 + m_2)ltM` तथा `m_3 a_4`, द्रव्यमानों के दो हल्के नाभिक पूर्ण संलयन करके, एक M' द्रव्यमान का भारी नाभिक बनाते हैं, यदि `(m_3+m_4)gtM'` | कुछ उदासीन परमाणुओं के द्रव्यमान नीचे टेबल में दिये गये है:

सही कथन है
View Solutionसूची I में कुछ नाभिकीय प्रक्रियाएँ दी गई है। सूची II में इन प्रक्रियाओं के जनक नामिक व एक अंतिम नाभिकीय खंड दिए गए हैं। सूचियों के नीचे दिये गए कोड का प्रयोग करके सही उत्तर चुनिए :

View Solutionकिसी धातु की एक सतह को अलग-अलग तरंगदैर्ध्य 248 nm तथा 310 nm से प्रदीप्त किया गया है। इन तरंगदैर्ध्य के संगत (corresponding) निकलने वाले प्रकाश इलेक्ट्रॉनों (photoelectrons) की अधिकतम गति क्रमशः `u_1` तथा `u_2`। यदि अनुपात :`u_1 : u_2 = 2 : 1` तथा hc = 1240eV nm है, तब धातु का कार्य फलन लगभग है:
View Solutionताँबे (परमाणु क्रमांक 29) की `K_(alpha)` X - किरण रेखा की तरंगदैर्घ्य `lambda_(Cu)` है तथा मॉलिब्डेनम (परमाणु क्रमांक 42) की `K_(alpha)` X-किरण रेखा की तरंगदैर्ध्य `lambda_(Ma)` है, तब अनुपात `lambda_(Cu)//lambda_(Mo)` लगभग है :
View Solutionएक गाँव को विद्युत ऊर्जा प्रदान करने वाले नाभिकीय संयंत्र में एक T वर्ष अर्द्ध-आयु के रेडियोधर्मी पदार्थ को ईंधन के रूप में प्रयोग किया जा रहा है। प्रारंभ में ईंधन की मात्रा इतनी है कि गाँव की सम्पूर्ण विद्युत शक्ति की आवश्यकताएँ उस समय उपलब्ध विद्युत शक्ति की 12.5% है। यदि यह संयत्र गाँव की सम्पूर्ण ऊर्जा आवश्यकताओं को अधिकतम nT वर्षों के लिए पूरा कर सकता है, तब n का मान है
View Solutionएक हाइड्रोजन परमाणु में इलेक्ट्रान n कक्षा में है। उसको आयनित करने के लिए 90 nm तरंगदैर्ध्य के विद्युत-चुबकीय विकिरण का प्रयोग किया जाता है। यदि इस प्रक्रिया में उत्सर्जित इलेक्ट्रॉन की गतिज ऊर्जा 10.4ev है, तब n का मान होगा (hc = 1242 eV nm)
View Solutionकॉलम-I में दी गयी नाभिकीय प्रक्रियाओं का कॉलम-II में दिये गये विकल्प/विकल्पों से उचित मिलान कीजिए
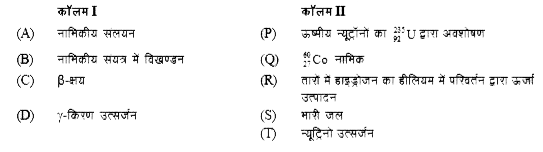
View Solution`Li^(2+)` आयन की उत्तेजित अवस्था में एक इलेक्ट्रॉन का कोणीय संवेग `3h//2pi` है। इस अवस्था में इलेक्ट्रॉन की डी-ब्रोग्ली तरंगदैर्ध्य `p pi a_0` (जहाँ `a_0` बोर त्रिज्या है) है । तब p का मान है
View Solutionएक रेडियोधर्मी पदार्थ की सक्रियता A एवं सक्रियता परिवर्तन की दर R क्रमशः `A = - (dN)/(dt)` तथा`R = (dA)/(dt)` संबन्धों द्वारा परिभाषित की जाती है, जहाँ समय । पर नाभिकों की संख्या N(t) है। दो रेडियोधर्मी स्त्रोत P(औसत आयु `tau`) तथा Q(औसत आयु `tau`) की समय t =0 पर समान सक्रियता है। उनकी सक्रियता परिवर्तन की दरें समय `t = 2tau` पर क्रमशः `R_p" तथा "R_Q` हैं। यदि `R_p/R_Q = n/e`, तब n का मान है:
View Solutionएक विखण्डन प्रक्रिया `""_(92)^236U to ""_(54)^140Xe + ""_(38)^(94)Sr + x + y`, दी गयी है, जहाँ x तथा y दो कण हैं। `""_(92)^236U` विरामावस्था में है तथा उत्पादों की गतिज ऊर्जाऐं क्रमशः `K_(Xe), K_(Sr), K_X (2MeV)" तथा "K_(y) (2MeV)` से दर्शायी गयी है। `""_92^236U,""_(54)^140Xe` तथा `""_38^94Sr` की प्रति न्यूक्लिऑन बंधन ऊर्जाओं को क्रमशः 7.5 MeV,8.5 MeV तथा 8.5 MeV लें। विभिन्न संरक्षण नियमों का ध्यान रखते हुए सही विकल्प है (हैं):
View Solutionप्लांक स्थिरांक निकालने के लिए एक एतिहासिक प्रयोग में एक धातु की सतह को अलग-अलग तरंगदैर्ध्य के प्रकाश से प्रदीप्त किया गया। उत्सर्जित प्रकाशिक इलेक्ट्रॉन की ऊर्जा को निरोधी विभव (stopping potential) लगाकर मापा गया। उपयोग में लाये गए आपतित प्रकाश की तरंगदैर्ध्य (`lambda `) एवं सम्बन्धित निरोधी विभय (`V_0`) के आंकड़े नीचे दिये गये हैं:
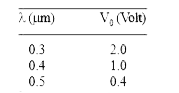
प्रकाश की गति `c = 3 xx 10^(8) ms^(-1)` तथा इलेक्ट्रॉन का आवेश `e = 1.6 xx 10^(-19)C` दिया गया है। इस प्रयोग से निकाले गए प्लांक स्थिरांक (Js मात्रक में) का मान है
View SolutionZe नाभिकीय आवेश के हाइड्रोजन की तरह के परमाणु की अत्यधिक उत्तेजित अवस्था (जिसे रिड्बर्ग अवस्था भी कहते हैं) को उसके मुख्य कांटम अंक n (n >> 1) से परिभाषित किया जाता है। निम्नलिखित में से कौनसा/कौनसे कथन सत्य है/हैं?
View Solutionएक हाइड्रोजन परमाणु को उसकी निम्नतम अवस्था में 970Å तरंगदैर्ध्य वाले प्रकाश से प्रदीप्त किया जाता है। यहाँ पर `hc//e = 1.237 xx 10^(-6)eVm` तथा हाइड्रोजन परमाणु की न्यूनतम अवस्था की ऊर्जा -13.60V है। उत्सजित मानावली (emission spectrum) में रेखाओं की संख्या क्या होगी?
View Solutionसमस्थानिक (isotope) `""_5^12B` जिसका द्रव्यमान 12.014u है, बीटा क्षय (`beta`-decay) की प्रक्रिया से `""_6^12C` में परिवर्तित हो जाता है। `""_6^12C` की एक नाभिकीय उत्तेजित अवस्था (`""_6^12C^**`) निम्नतम अवस्था से 4.041 MeV ऊपर होती है। अगर `""_5^12B` क्षय होकर `""_6^12C^(**)` में परिवर्तित होता है तो बीटा कण की अधिकतम गतिक ऊर्जा (MeV की मात्रा में) क्या होगी ? (`1 u = 931.5 MeV //c^2`, यहाँ c निर्वात में प्रकाश की गति है)
View Solutionत्रिज्या R वाले एक गोलाकार नाभिक (nucleus) में Z प्रोटोन समानरूप से वितरित है। ऐसे नाभिक की स्थिर विद्युत ऊर्जा नीचे समीकरण में दी गई है
`E =3/5 (Z (Z-1)e^2)/(4 pi epsi_0R)`
न्यूट्रॉन, `""_1^1H, ""_7^15N" एवं ""_8^15O` नाभिकों (nuclei) के मापे गये द्रव्यमान क्रमशः 1.008665 u, 1.007825 u, 15.000109 u एवं 15.003065 u हैं। `""_7^15N" और ""_8^15O`नाभिकों की त्रिज्यायें समान दी गई हैं। `1u = 931.5 MeV//c^2` (जहाँ पर प्रकाश की गति है) और `e^2//(4pi epsi_0) =1.44 MeV fm` यदि `""_7^15N" और ""_8^15O` की बंधक ऊर्जाओं का अंतर सिर्फ स्थिर विदयुत ऊर्जा के कारण है, तो दोनों में से किसी भी नाभिक की त्रिज्या क्या होगी `(1 fm =10^(-15)m)`
View Solutionएक नाभिकीय प्रयोगशाला में दुर्घटना की वजह से रेडियोएक्टिव पदार्थ की कुछ मात्रा जमा हो गयी, जिसकी अर्धायु 18 दिनों की है। परीक्षण से पता चला कि प्रयोगशाला में विकिरण का स्तर सुरक्षित स्तर से 64 गुणा ज्यादा था। न्यूनतम कितने दिनों के बाद प्रयोगशाला काम करने के लिए सुरक्षित होगी?
View Solution`lambda_(ph)` तरंगदैर्ध्य का प्रकाश निर्वात नलीका (vacuum tube) के अंदर एक कैथोड पर गिरता है, जैसा चित्र में दर्शाया गया है। कैथोड की सतह का कार्यफलन `phi` है एवं एनोड, जो की एक चालकीय पदार्थ के तारों की जाली है, कैथोड से d दूरी पर स्थित है। एलेक्ट्रोडों के बीच का विभवान्तर V स्थिर है। यदि एनोड को पार करने वाले इलेक्ट्रॉनों की न्यूनतम "द ब्रोग्ली" (de Broglie) तरंगदैर्ध्य `lambda_e` है, निम्नलिखित में से कौनसा/ कौनसे कथन सत्य है/हैं?
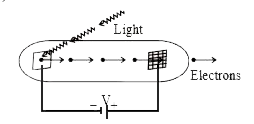
View Solutionएक हाइड्रोजन परमाणु का एक इलेक्ट्रॉन `n_i` क्वांटम संख्या (quantum number)क वाले कक्ष से `n_f` क्वांटम संख्या (quantum number) के कक्षा में प्रवेश करता है। `V_i` तथा `V_f` प्राथमिक एवं अंतिम स्थितिज उर्जाए है। यदि `v_i/v_f= 6.05`, तब `n_f` की न्यूनतम सम्भावी संख्या (smallest possible `n_f`) है
View Solutionआयोडीन का समस्थानिक (isotope)। जिसकी अर्ध-आधु 8 दिन है. `beta`-क्षय के कारण जेनॉन (Xenon) के समस्थानिक में क्षयिक होता है। अल्प मात्रा का `""^(131)I`चिहित (labelled) सीरम (serum) मानव शरीर में अन्तक्षिप्त (imject) किया गया, जिस मात्रा की ऑक्टिवता (activity) `2.4 xx 10^5` बेकरेल (Becquere) है। यह सीमर रूधिर धारा में आधे घंटे में एकसमान वितरित होता है। अगर 11.5 घंटे बार 2.5 ml रक्त 115 बेकरेल की ऑक्टिवता दर्शाता है, तब मानव शरीर में रक्त आयतन (लीटर में) है (आप `e^x ~~ 1 + x " for " absx lt lt1 " एवं "ln2~~0.7` का उपयोग कर कसते हैं)
View Solutionप्रकाश विद्युत पदार्थ (photoelectric material) जिसका कार्य फलन (work - function) on है, तरंग दैर्ध्य `lambda(lambda lt (hc)/(phi_0))` के प्रकाश के प्रदीप्त किया गया है। दुत प्रकाश इलेक्ट्रॉन की डी ब्रोग्ली (de Broglie) तरंगदैर्ध्य `lambda_d` है। आपतित प्रकाश (incident light) की तरंगदैर्ध्य में `Delta lambda` के परिवर्तन से `lambda_d` के मान में `Delta lambda`के परिवर्तन से`lambda_d` के मान में `Delta lambda_d` का परिवर्तन होता है। तब `Delta lambda_d //Delta lambda` का अनुपात समानुपाती होगा
View Solution
EXERCISE - 4 (JEE ADVANCED Previous Year.s Questions) questions and complete solutions for chapter आधुनिक भौतिकी of BANSAL PHYSICS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 PHYSICS आधुनिक भौतिकी
- EXERCISE - 1 (OBJECTIVE QUESTIONS) (MULTIPLE CORRECT CHOICE TYPE)
- EXERCISE - 1 (OBJECTIVE QUESTIONS) (PARAGRAPH TYPE)
- EXERCISE - 1 (OBJECTIVE QUESTIONS) (REASONING TYPE)
- EXERCISE - 1 (OBJECTIVE QUESTIONS) (SINGLE CORRECT CHOICE TYPE)
- EXERCISE - 4 (JEE ADVANCED Previous Year.s Questions)
- EXERCISE - 5 (CBSE Previous Year.s Questions)
- EXERCISE-2 (Subjective Questions)
- EXERCISE-3 (JEE Main Previous Year.s Questions)