Complete Solutions to खण्ड-I (वस्तुनिष्ट प्रश्न) of chapter भौतिक विज्ञान -2009 of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | भौतिक विज्ञान -2009 |
| BIHAR BOARD- PREVIOUS YEAR PAPER | खण्ड-I (वस्तुनिष्ट प्रश्न) |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
कूलम्ब बल है :
View Solutionयदि समरूप विद्युत क्षेत्र X- अक्ष की दिशा में विघमान है , तो सम - विभव होगा :
View Solutionकिसी विभवमापी की संवेदनशीलता को बढ़ाने के लिए।
View SolutionA क्षेत्रफल के वृत्तिय पाश के केंद्र पर चुम्ब्कीय क्षेत्र B है तो उस पाश का चुम्ब्कीय आघूर्ण होगा :
View Solutionयदि L प्रेरकत्व, R प्रतिरोध तथा C संधारित्र की धारिता हो , तो `(L)/(R )` एवं RC का विमीय सूत्र है :
View Solutionचुंबक के अक्षीय स्थिति निरक्षीय स्थिति में अंतर स्थिति में d दूरी पर चुंबकीय क्षेत्र यदि क्रमश: `B_(1)` तथा `B_(2)` हों , तो
View Solutionविद्युत चुम्ब्कीय तरंग में विद्युतीय एवं चुम्ब्कीय क्षेत्रों के बीच कलान्तर होता है :
View Solutionस्काई वेब संचार आधारित है :
View Solutionमॉडुलन का सही जोड़ा चुने :
(a) आयाम मॉडुलन : (i) आयाम : मॉडुलन संकेत
(b) आवृति मॉडुलन : (ii) आरभिक कला : मॉडुलन संकेत
View Solutionमूल गेट ( बेसिक गेट ) है :
View Solutionनिम्नलिखित कथनों की विवेचना करें :
कथन I : विद्युतीय बल - रेखाएँ एक दूसरे को नहीं काटती है।
कथन II : बल - रेखा के किसी बिन्दु पर खींची गई स्पर्श रेखा की दिशा , उस बिन्दु पर क्षेत्र की तीव्रता को दर्शाता है।
View Solutionनिम्नलिखित कथनों की विवेचना करें :
कथन (I) चित्र में दिखाया गया डायोड एक जेनर डायोड है।
चित्र में दिखाया गया डायोड एक जेनर डायोड है।
कथन (II) जीनर डायोड पश्च अभिनति (रिवर्स बायस) के सिद्धांत पर काम करता है।
View Solutionनिम्नलिखित कथनों की विवेचना करें :
कथन I : गैल्वेनोमीटर , एमीटर , तथा वोल्टमीटर में से सबसे अधिक प्रतिरोध वोल्टमीटर का होता है , तथा सबसे कम एमीटर का।
कथन II : किसी परिपथ में एमीटर को सर्वदा श्रेणीक्रम में तथा वोल्टमीटर को समान्तर क्रम में जोड़ा जाता है।
View Solutionनिम्नलिखित कथनों की विवेचना करें :
कथन I: विद्युत - चुम्बकीय तरंगों में विद्युत क्षेत्र `(vec(E))` का साम्यर्थ चुम्बकीय क्षेत्र `(vec(B))` से काफी अधिक रहता है।
कथन II : विद्युत - चुम्बकीय तरंग लंबवत विद्युत क्षेत्र में विक्षेपित होती है , लेकिन लंबवत चुम्बकीय क्षेत्र अविक्षेपित रहती है।
View Solutionनिम्नलिखित कथनों की विवेचना करें :
कथन I : वाट के लेजर किरण से धातु के पत्तर में छेद हो जाता है , जबकि 1000 वाट की टार्च लाइट से छेद नहीं हो पाता है।
कथन II : लेजर प्रकाश की आवृति व वेग , टार्च के प्रकाश की आवृति व वेग से बहुत अधिक होती है।
View Solutionयांत्रिकीय ऊर्जा को वैधुतिक ऊर्जा में बदलने के लिए , हमे प्रयोग करना है :
View Solutionएक प्रतिरोधक के आरपार प्रत्यावर्ती धारा वोल्टता मापी जा सकती है :
View Solutionजैसी - जैसी द्रव्यमान संख्या A बढ़ती है , उसी के साथ -साथ निम्न में से न्यूक्लिअस से सम्बन्धित किस राशि का परिवर्तन नहीं होता है ?
View Solution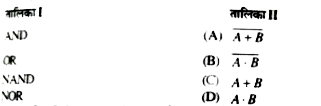
View Solution
View Solution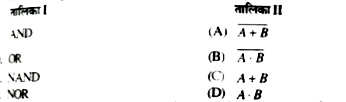
View Solution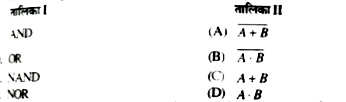
View Solution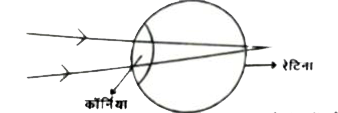
चित्र में आँख की बनावट का एक सरलीकृत स्वरुप दिया गया है , जिसमे आँख पर आपतित पूरे प्रकाश के अपवर्तन को कॉर्निया से होता माना जाता है। कॉर्निया आँख का सबसे अगला भाग है , जो लगभग 2 सेमी के एक नियत फोकस दूरी वाली अभिसारी लेंस होता है। अनन्त से आनेवाली समानान्तर किरणें कॉर्निया से अपवर्तित होकर रेटिना पर फोकसित प्रतिबिम्ब बनाती है। रेटिना प्रतिबिम्ब बनने की सूचना को प्रकाश तंत्रिका के माध्यम से मस्तिष्क तक पहुँचाती है।
निकट दिष्टि दोष एवं दूर दोष आँख में होने वाले दो समान्तर बीमारियाँ है। निकट दिष्टि दोष या मायोपिया में दूर से आने वाली किरणें कॉर्निया से अपवर्तन के बाद दूरस्थ वस्तु का प्रतिबिम्ब रेटिना के सम्मुख बना देती है। दूर दिष्टि दोष या हाइपरोपिया में नजदीक की वस्तु का प्रतिबिम्ब कॉर्निया से अपवर्तन के बाद रेटिना से पीछे बनता है। दोनों दोषों को दूर करने के लिए उपयुक्त फोकस दूरी एवं प्रकृति का लेंस प्रयोग किया जाता है। कॉर्निया तथा प्रयुक्त लेंस का संयुक्त समूहन प्रतिबिम्ब को पुनः रेटिना पर ले आता है। यदि दूर की वस्तु को अनन्त पर मान जाए तब कॉर्निया से प्रतिबिम्ब की दूरी को निम्नलिखित सूत्र से ज्ञात किया जा सकता है :
`(1)/(f_c)+(1)/(f_(1)-x)=(1)/(v),f_(c)=` कॉर्निया की फोकस - दूरी
`f_(1)=` संशोधी लेंस की फोकस - दूरी
`x=` कॉर्निया एवं अतिरिक्त लेंस के बीच की दूरी
सामान्य दोषमुक्त आखों में कॉर्निया से कितनी दूरी पर रेटिना होना चाहिए ?
View Solution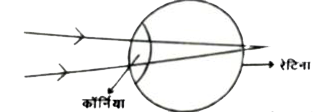
चित्र में आँख की बनावट का एक सरलीकृत स्वरुप दिया गया है , जिसमे आँख पर आपतित पूरे प्रकाश के अपवर्तन को कॉर्निया से होता माना जाता है। कॉर्निया आँख का सबसे अगला भाग है , जो लगभग 2 सेमी के एक नियत फोकस दूरी वाली अभिसारी लेंस होता है। अनन्त से आनेवाली समानान्तर किरणें कॉर्निया से अपवर्तित होकर रेटिना पर फोकसित प्रतिबिम्ब बनाती है। रेटिना प्रतिबिम्ब बनने की सूचना को प्रकाश तंत्रिका के माध्यम से मस्तिष्क तक पहुँचाती है।
निकट दिष्टि दोष एवं दूर दोष आँख में होने वाले दो समान्तर बीमारियाँ है। निकट दिष्टि दोष या मायोपिया में दूर से आने वाली किरणें कॉर्निया से अपवर्तन के बाद दूरस्थ वस्तु का प्रतिबिम्ब रेटिना के सम्मुख बना देती है। दूर दिष्टि दोष या हाइपरोपिया में नजदीक की वस्तु का प्रतिबिम्ब कॉर्निया से अपवर्तन के बाद रेटिना से पीछे बनता है। दोनों दोषों को दूर करने के लिए उपयुक्त फोकस दूरी एवं प्रकृति का लेंस प्रयोग किया जाता है। कॉर्निया तथा प्रयुक्त लेंस का संयुक्त समूहन प्रतिबिम्ब को पुनः रेटिना पर ले आता है। यदि दूर की वस्तु को अनन्त पर मान जाए तब कॉर्निया से प्रतिबिम्ब की दूरी को निम्नलिखित सूत्र से ज्ञात किया जा सकता है :
`(1)/(f_c)+(1)/(f_(1)-x)=(1)/(v),f_(c)=` कॉर्निया की फोकस - दूरी
`f_(1)=` संशोधी लेंस की फोकस - दूरी
`x=` कॉर्निया एवं अतिरिक्त लेंस के बीच की दूरी
निकट दिष्टि एवं दूरी दिष्टि दोष को दूर करने के लिए क्रमशः किस प्रकृति का लेंस उपयोग किया जाना चाहिए ? [ मान लें कि `f_(c)=x`]
View Solution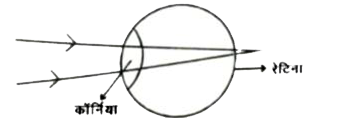
चित्र में आँख की बनावट का एक सरलीकृत स्वरुप दिया गया है , जिसमे आँख पर आपतित पूरे प्रकाश के अपवर्तन को कॉर्निया से होता माना जाता है। कॉर्निया आँख का सबसे अगला भाग है , जो लगभग 2 सेमी के एक नियत फोकस दूरी वाली अभिसारी लेंस होता है। अनन्त से आनेवाली समानान्तर किरणें कॉर्निया से अपवर्तित होकर रेटिना पर फोकसित प्रतिबिम्ब बनाती है। रेटिना प्रतिबिम्ब बनने की सूचना को प्रकाश तंत्रिका के माध्यम से मस्तिष्क तक पहुँचाती है।
निकट दिष्टि दोष एवं दूर दोष आँख में होने वाले दो समान्तर बीमारियाँ है। निकट दिष्टि दोष या मायोपिया में दूर से आने वाली किरणें कॉर्निया से अपवर्तन के बाद दूरस्थ वस्तु का प्रतिबिम्ब रेटिना के सम्मुख बना देती है। दूर दिष्टि दोष या हाइपरोपिया में नजदीक की वस्तु का प्रतिबिम्ब कॉर्निया से अपवर्तन के बाद रेटिना से पीछे बनता है। दोनों दोषों को दूर करने के लिए उपयुक्त फोकस दूरी एवं प्रकृति का लेंस प्रयोग किया जाता है। कॉर्निया तथा प्रयुक्त लेंस का संयुक्त समूहन प्रतिबिम्ब को पुनः रेटिना पर ले आता है। यदि दूर की वस्तु को अनन्त पर मान जाए तब कॉर्निया से प्रतिबिम्ब की दूरी को निम्नलिखित सूत्र से ज्ञात किया जा सकता है :
`(1)/(f_c)+(1)/(f_(1)-x)=(1)/(v),f_(c)=` कॉर्निया की फोकस - दूरी
`f_(1)=` संशोधी लेंस की फोकस - दूरी
`x=` कॉर्निया एवं अतिरिक्त लेंस के बीच की दूरी
एक व्यक्ति के कॉर्निया की फोकस दूरी 1.8 सेमी है , तथा वह दिष्टीदोष से मुक्त हेतु एक `f=-16.5` सेमी के संशोधी लेंस को आंख के कॉर्निया से `x=1.5` सेमी की दूरी पर उपयोग करता है। ऐसी स्थिति में दूरस्थ वस्तु से आने वाली किरणों का कॉर्निया से प्रतिबिम्ब दूरी होगी :
View Solution
खण्ड-I (वस्तुनिष्ट प्रश्न) questions and complete solutions for chapter भौतिक विज्ञान -2009 of BIHAR BOARD- PREVIOUS YEAR PAPER of Class 12