Complete Solutions to MATHEMATICS of chapter QUESTION-PAPERS-2014 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | QUESTION-PAPERS-2014 |
| BITSAT GUIDE | MATHEMATICS |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
The set `(A-B) cup (B-A)` is equal to
View SolutionThe domain of definition of `f(x)=log_(2)( -log_(1//2) (1+(1)/(x^(1//4)))-1)` is :
View Solution`cos^2 (pi/6 + theta) - sin^2 (pi/6 - theta) =`
View SolutionThe solution of (2 cos x – 1) (3 + 2 cos x) = 0 in the interval `0 lt= x lt= 2pi` is
View Solution`2^(3n)-7n-1` is divisible by
View SolutionThe greatest positive integer, which divides n(n+1)(n+2)(n+3) for all `n in N` , is
View Solution`z=x+iy,z^(1/3)=a-ib,(x)/(a)-(y)/(b)=k(a^(2)-b^(2))` then k is :
View Solution` i^(57) + 1// i^(125)` , when simplified has the value
View SolutionThe complex number z =x+iy which satisfies the equation `| ( z - 3i )/( z + 3i ) | = 1,` then on
View SolutionThe number of all three elements subsets of the set `{a_1, a_2, a_3 ….a_n}` which contain `a_3` is
View SolutionIn how many ways can a committee of 5 made out 6 men and 4 women containing atleast one woman?
View SolutionFind the coefficient of `x^(4)` in the expansion of `(1+x+x^(2)+x^(3))^(11)`.
View SolutionIf `t_0,t_1, t_2,...,t_n` are the terms in the expansion of `(x+a)^n` then prove that `(t_0-t_2+t_4-...)^2+(t_1-t_3+t_5-...)^2=(x^2+a^2)^n`.
View SolutionIf the `(2p)^(th)` term of a H.P. is q and the `(2q)^(th)` term is p, then the `2(p + q)^(th)` term is-
View SolutionIf `1/a, 1/b,1/c ` are in A.P., the `(1/a + 1/b - 1/c) ( 1/b+1/c-1/a)` is equal to
View SolutionThe product of n positive numbers is unity. Then their sum is:
View SolutionIf `p_(1) and p_(2)` are the lengths of the perpendicular form the orgin to the line `x sec theta+y cosec theta=a and xcostheta-y sin theta=a cos 2 theta` respectively then prove that `4p_(1)^(2)+p_(2)^(2)=a^(2)`
View SolutionThe angle of intersection of the two circles `x^2 + y^2 - 2x - 2y = 0 and x^2 + y^2 = 4` , is
View SolutionIn a model, it is shown that an arc of a bridge in semi-elliptical with major axis horizontal. If the length of the base is 9 m and the highest part of the bridge is 3 m from the horizontal, the best approximation of the height of the arch at 2 m from the centre of the base is
View Solution`lim_(x rarr 0) (cosec x )^(1//"log"x)` is equal to
View SolutionIf M. D. is 12, the value of S.D. will be
View SolutionA bag contains 5 brown and 4 white socks. A man pulls out 2 socks. Find the probability that they are of the same colour.
View SolutionLet R= {(3, 3),(6,6), (9,9), (12, 12),(6, 12),(3,9), (3, 12), (3, 6)} be a relation on the set A={3,6,9,12}. The relation is:
View SolutionLet f : R - {n} `rarr` R be a function defined by `f(x)=(x-m)/(x-n)`, where `m ne n`. Then,
View SolutionThe value of tan `(2 "tan"^(-1)(1)/(5)-(pi)/(4))` is
View SolutionIf `[(alpha, beta),(gamma,-alpha)]` is to be square root of the two rowed unit matrix, then `alpha, beta` and `gamma` satisfy the relation
View SolutionFind the value of `lambda` , if the line `3x-4y-13=0,8x-11 y-33=0a n d2x-3y+lambda=0` are concurrent.
View Solution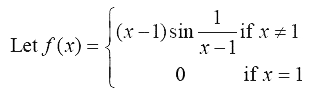
Then which one of the following is true?
View SolutionThe interval in which the function `2x^3 + 15` increases less rapidly than the function `9x^2 - 12x,` is –
View SolutionThe fuel charges for running a train are proportional to the square of the speed generated in miles per hour and costs 48 per hour at 16 miles per hour. The most economical speed if the fixed charges i.e. salaries etc. amount to 300 per hour is
View SolutionEvaluate: `int (1)/(1 + 3 sin^2 x + 8 cos^2x ) dx`
View Solution`int_0^10 (x^10)/((10 - x)^10 + x^10)` dx is equal to
View SolutionThe area bounded by the x-axis, the curve y=f(x) and the lines x =1, x =b, is equal to `sqrt(b^2 +1) - sqrt2` for all `b gt 1`, then f(x) is
View SolutionSolution of differential equation
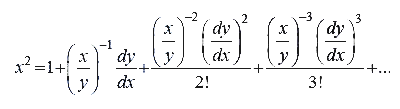
View SolutionIf the middle points of sides BC, CA and AB of triangle ABC are respectively D,E ,F then position vector of centre of triangle DEF, when position vector of A, B , C are respectively `hati + hatj, hatj + hatk , hatk + hati ` is
View SolutionFind the angel between any two diagonals of a cube.
View SolutionFind the angle between the line `(x+1)/2=y/3=(z-3)/6`and the plane `10 x + 2y -11 z = 3`.
View SolutionThe equation of the right bisector plane of the segment joining (2, 3, 4) and (6, 7, 8) is
View SolutionA bag contains `n+1` coins. If is known that one of these coins shows heads on both sides, whereas the other coins are fair. One coin is selected at random and tossed. If the probability that toss results in heads is 7/12, then find the value of `ndot`
View SolutionA coin is tossed 7 times.Each time a man calls head.The probability that he wins the toss on more occasions is
View SolutionConsider `x/2 + y/4 gt= 1 and x/3 + y/2 lt=1 ,x,y gt=0` number of possible solutions are :
View SolutionIf `A=[(1,1),(1,1)]` ,then `A^(100)` is equal to
View SolutionIf `|(p,q-y,r-z),(p-x,q,r-z),(p-x,q-y,r)|` = 0 then the value of `p/x+q/y+r/z` is
View SolutionThrough the vertex O of a parabola `y^2 = 4x` chords OP and OQ are drawn at right angles to one-another. Then for all positions of P, PQ cuts the axis of the parabola at a fixed point and the locus of the middle point of PQ is
View Solution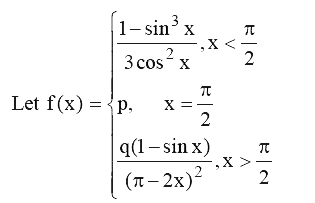
If f(x) is continous at x ` = pi/2, (p,q) = `
View Solution
MATHEMATICS questions and complete solutions for chapter QUESTION-PAPERS-2014 of BITSAT GUIDE of Class 12