Complete Solutions to EXAMPLE of chapter RELATIONS AND FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| BODY BOOKS PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Let T be the set of all triangles in a plane with R a relation in T given by `{(T_1,T_2):T_1~=T_2}`show that R is an equivalence relation.
View Solution* be a binary operation on Q,defined as `a**b=(3ab)/5` .Show that *is commutative.
View Solution*be a binary operation on Q,defined as `a**b=(3ab)/5` .Show that * is associative.
View Solution*be a binary operation on Q,defined as `a**b=(3ab)/5` Find the identity element of *if any.
View SolutionConsider the following functions.`f:ZrarrZ`defined by `f(x)=3x+7`
and `g:RrarrR` defind by `g(x)=2x-3`. Of the above two functions
one is a bijective function and the other is not.Give reason.
View SolutionWhich of the relations R on the set of the real numbers is an equivalence relation?
`(a).x R y` if `|x|=|y|`
View SolutionWhich of the relations R on the set of the real numbers is an equivalence relation?
`(b) x R y` if `x-yge0`
View SolutionIn the set of all natural numbers,let a relation defined by `{(a,b):a,binN,a-b` is divisible by `5}`.Prove that R is an equivalence relation.
View SolutionIf `f:RrarrR` is given by `f(x)=3x-1`,`g:RrarrR` is given by `g(x)=2x`,show that `fog-gof=1`.
View SolutionFind the domain,range and inverse of `f:xrarr(x-3)/(2x+1) `.
View SolutionProve that the function `f: N rarr N` , defined by
`f(x)=x^2+x+1` is one-one but not onto.
View SolutionConsider the binary operation * on the set {1,2,3,4,5} given by the following table(i)Is * commutative?.
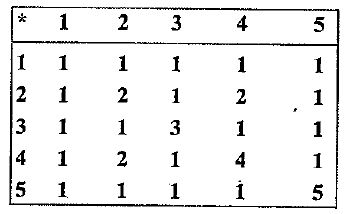
View SolutionConsider the binary operation * on the set {1,2,3,4,5} given by the following table.(ii)Compute (2*3)*4 and2*(3*4).
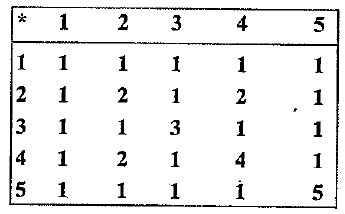
View SolutionConsider the binary operation * on the set {1,2,3,4,5} given by the following table.iii) Compute (2*3)*(4*5).
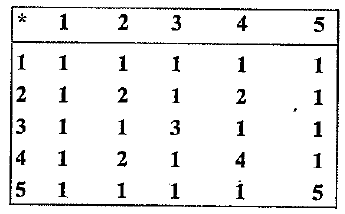
View SolutionLet * be a binary operation on N,defined bya*b=`a^b,a,binN`.is * associative or commutative?
View SolutionIf the following `f:RrarrR`is given by `f(x)=(x+3)/3` and` g:RrarrR` is given by g(x)=2x-3.Find fog
View SolutionIf the following `f:RrarrR`is given by `f(x)=(x+3)/3` and` g:RrarrR` is given by `g(x)=2x-3`.Find gof
View SolutionIf the following `f:RrarrR`is given by `f(x)=(x+3)/3` and` g:RrarrR` is given by `g(x)=2x-3`.Is `f^(-1)=g`
View SolutionConsider `f:R_+ rarr[-5,infty)`given by `f(x)=9x^2+6x-5`.Show that f is invertible with `f^-1(y)=((sqrt(y+6)-1)/3)`
View SolutionA is a non empty set and let*be a binary operation an P(A)the prower set of A defined by `X**Y=XcapY` for X,`YinP(A)`(i) Show that A*B=B* A for A,`BinP(A)`
View SolutionA is a non empty set and let*be a binary operation an P(A)the prower set of A defined by `X**Y=XcapY` for X,`YinP(A)`(ii)Show that * is associative.
View SolutionLet S be the set of all sets and let `R={(A,B):AsubsetB}` i.e A is a proper subset of B.Show that R is (i).Transitive
View SolutionLet S be the set of all sets and let `R={(A,B):AsubsetB}` i.e A is a proper subset of B.Show that R is Not reflexive
View SolutionLet S be the set of all sets and let `R={(A,B):AsubsetB}` i.e A is a proper subset of B.Show that R is not symmetric
View SolutionProve that the function`f:NrarrN` f(x)=3x,is one -one and into.
View SolutionIf f:`RrarrR` be defined by `f(x)=2x-3`and `g:RrarrR` be defined by `g(x)=(x+3)/2`.Show that `fog=I_R=gof`
View SolutionIf f:`RrarrR` be defined by f(x)=3x+2.Show that f is invertible.Find `f^-1:RrarrR`.Hence find `f^-1(3)`and `f^-1(0)`
View SolutionConsider the binary operation `**:QrarrQ`,where Q is the set of rational numbers,is defined as a*b=a+b-ab.(i).Is * associative?Justify your answer.
View SolutionConsider the binary operation `ast` : `QtoQ` where Q is the set of rational numbers as defined as `aastb=a+b-ab`
Is identity for `ast` exist? If yes, find the identity element.
View SolutionConsider the binary operation `ast` : `QtoQ` where Q is the set of rational numbers as defined as `aastb=a+b-ab`
Are elements of Q invertible? Is yes, find the inverse of an element in Q
View SolutionA fuction`f:RrarrR` defined by`f(x)=(2x-3)/7` .Is f a one-one function?Why?
View SolutionA fuction`f:RrarrR` defined by`f(x)=(2x-3)/7` ii.Prove that f is invertible.
View SolutionA fuction`f:RrarrR` defined by`f(x)=(2x-3)/7` .
Find`f^-1`
View SolutionShow that the relation 'S' in set `A={x inz:0lexle12}` given by S={(a,b):a.bin z,|a-b|`is divisble by a} is an equivalence relation.
View SolutionLet `f:{1,2,3}rarr{3,5,7}` and `g:{3,5,7}rarr{7,23,47}`given by f(1)=3,f(2)=5,f(3)=,g(3)=7,g(5)=23,g(7)=47 (i).Find gof
View SolutionLet Q be the set of Rational numbers and '`ast`' be the binary operation on Q defined by '`aastb=frac(ab)(4)`' for all a,b in Q.
Find the inverse element of '`ast`' on Q.
View SolutionLet Q be the set of Rational numbers and '`ast`' be the binary operation on Q defined by '`aastb=frac(ab)(4)`' for all a,b in Q.
Find the inverse element of '`ast`' on Q.
View SolutionShow that the function `f:RtoR` defined by `f(x)=2x-3` is one-one and onto. Find `f^-1`
View SolutionWhich of the following figure represents the graph of a function on R which is onto but not one-one.

View Solution`A={1,2,3,4,6},ast` is a binary operation on A is defined as `aastb=HCF` of a and b.
Represent `ast` with the help of an operation table.
View Solution`A={1,2,3,4,6},ast` is a binary operation on A is defined as `aastb=HCF` of a and b.
Find the identity element.
View Solution`A={1,2,3,4,6},ast` is a binary operation on A is defined as `aastb=HCF` of a and b. Draw its operation table.
Write a commutative binary operation on A with 3 as the identity element. ( Hint: Operation table may be used.
View SolutionGive an example of a relation which is reflexive but not symmetric
View SolutionGive an example of a relation which is transitive but not symmetric
View SolutionLet A={3,5} and B={7,11}.Let `R={(a,b):ainA,binB,a-b` is odd}.Show that R is an empty relation from A into B.
View SolutionLet * be a binary operation on setQ of rational numbers such that `a**b=(2a-b)^2:a,binQ` i.Find 3*5
View SolutionIf `f : R rarr R` be given by f(x) = `(3 - x^3)^(1/3)`, then (f o f) (x) is
View SolutionLet * be the binary operation on N given by x*y=LCM of x,y.Find 9*5?
View SolutionLet `A=NtimesN` and '`ast`' be the binary operation. On A defined by `(a,b)ast(c,d)=(a+c,b+d)`. Show that '`ast`' is commutative and associative. Find the identity for '`ast`' on A if any.
View SolutionShow that the function f in `A=R-{2/3}`defined as `f(x)=(4x+3)/(6x-4)` is one-one and onto.
View SolutionShow that the function f in `A=R-{2/3}`defined as `f(x)=(4x+3)/(6x-4)` is one-one and onto.Hence find `f^-1`
View SolutionIf `R_1` and `R_2` are equivalence relations in a set A, show that `R_1 nn R_2` is also an equivalence relation.
View SolutionConsider the set `A={1,2,3,4,5}`, and `B={1,4,9,16,25}` and a function `f:AtoB` defined by `f(1)=1`, `f(2)=4`, `f(3)=9`, `f(4)=16 ` and `f(5)=25`.
Show that `f` is one-to-one.
View SolutionConsider the set `A={1,2,3,4,5}`, and `B={1,4,9,16,25}` and a function `f:AtoB` defined by `f(1)=1`, `f(2)=4`, `f(3)=9`, `f(4)=16 ` and `f(5)=25`.
Show that `f` is onto.
View SolutionConsider the set `A={1,2,3,4,5}`, and `B={1,4,9,16,25}` and a function `f:AtoB` defined by `f(1)=1`, `f(2)=4`, `f(3)=9`, `f(4)=16 ` and `f(5)=25`.
Does `f^-1` exists? Explain.
View SolutionLet `f:RtoR` be given by `f(x)=frac(2x+1)(3)` find
`fof` and show that `f` is invertible.
View SolutionLet R be a Relation in the set
`A={1,2,3,4,5,6}` define as
`R={(x,y):y=2x-1}`
Write R in roster form and find it's domain and range
View SolutionLet R be a Relation in the set
`A={1,2,3,4,5,6}` define as
`R={(x,y):y=2x-1}`
Is R an equivalance relation? Justify.
View SolutionThe relation R defined on the A={-1,0,1} as `R={(a,b):a^2=b}`
Check whether R is reflexive,symmetric and transitive
View SolutionThe relation R defined on the A={-1,0,1} as `R={(a,b):a^2=b}`
Check whether R is reflexive,symmetric and transitive
View SolutionLet `A={1,2,3}`. Give an example of a relation on A which is
Symmetric but neither reflexive nor transitive.
View SolutionLet `A={1,2,3}`. Give an example of a relation on A which is
Transitive but neither reflexive nor symmetric.
View SolutionLet be a function defined by `f(x) =sqrtx` is a function if it defined from f : N`to`N`
View SolutionCheck the injectivity and surjectivity of the following functions
`f:NtoN` defined by `f(x)=x^3`
View SolutionCheck the injectivity and surjectivity of the following functions
`f:RtoR` given by `f(x)=[x]`
View SolutionFind fog and gof if `f(x)=|x|` and `g(x)=|3x+4|`
View SolutionFind fog and gof if `f(x)=16x^4` and `g(x)=x^(3/4)`
View SolutionIf `f(x)=frac(4x+3)(6x-4),xne2/3`.
Show that `fof(x)=x`, for all `xne2/3`.
View SolutionLet S={(1,2),(2,3),(3,4)}.Find the domain and range of S.
View SolutionLet S={(1,2),(2,3),(3,4)}. Find `S^-1`
View SolutionLet S={(1,2),(2,3),(3,4)}. Find the domain and range os `S^-1`
View SolutionConsider `f:{3,4,5,6}to{8,10,12,13,14}` and `f={(3,8),(4,10),(5,12),(6,14)}`. State whether `f` has inverse? Give reason.
View SolutionConsider `f:RtoR` given by
`f(x)=3x+2` show that `f` is invertible. Find the inverse of `f`
View SolutionChoose the correct answer from the bracket.If `x!=1`and `f(x)=(x+1)/(x-1)` is a real function,then fof(2)=______(1,2,3,4) and What is the inverse of f.
View SolutionChoose the correct answer from the bracket.If `x!=1`and `f(x)=(x+1)/(x-1)` is a real function,then fof(2)=______(1,2,3,4).Find `f(3)+f^-1(3)`
View SolutionDetermine whether the following is a binary operation or not?Justify `a**b=2^(ab)`defined on Z
View SolutionDetermine whether * is commutative or associative if `a**b=(ab)/6,a,bnotinR`
View SolutionConsider the binary operation `ast` : `QtoQ` where Q is the set of rational numbers as defined as `aastb=a+b-ab`
Find `2ast3`
View SolutionConsider the binary operation `ast` : `QtoQ` where Q is the set of rational numbers as defined as `aastb=a+b-ab`
Is identity for `ast` exist? If yes, find the identity element.
View SolutionConsider the binary operation `ast` : `QtoQ` where Q is the set of rational numbers as defined as `aastb=a+b-ab`
Are elements of Q invertible? Is yes, find the inverse of an element in Q
View SolutionState the reason for the relation R in the set {1,2,3}given by R={(1,2),(2,1)}not to be transitive.
View SolutionShow that the function f in `A=R-{2/3}`defined as `f(x)=(4x+3)/(6x-4)` is one-one and onto.Hence find `f^-1`
View SolutionLet `R` be `a`.relation from `Q` to `Q` defined by `R={(a, b): a, b in Q` and `a-b in Z }.` Show that
i) `(a, a) in R` for all `a in Q`
ii) `(a, b) in R` implies that `(b, a) in R`
iii) `(a, b) in R` and `(b, c) in R` implies that `(a, c) in R .`
View SolutionLet `R` be `a`.relation from `Q` to `Q` defined by `R={(a, b): a, b in Q` and `a-b in Z }.` Show that
i) `(a, a) in R` for all `a in Q`
ii) `(a, b) in R` implies that `(b, a) in R`
iii) `(a, b) in R` and `(b, c) in R` implies that `(a, c) in R .`
View SolutionLet `R` be `a`.relation from `Q` to `Q` defined by `R={(a, b): a, b in Q` and `a-b in Z }.` Show that
i) `(a, a) in R` for all `a in Q`
ii) `(a, b) in R` implies that `(b, a) in R`
iii) `(a, b) in R` and `(b, c) in R` implies that `(a, c) in R .`
View SolutionIn each of the following cases, states whether the function is one-one,
onto or bijective. Justify your answer. `f : R rarr R` defined by f(x) =3 - 4x
View SolutionIn each of the following cases, states whether the function is one-one,
onto or bijective. Justify your answer. `f : R rarr R` defined by f(x) = ` 1 + x^2`
View SolutionIn each of the following cases,state whether the function is onto,one to one or bijective.Justify your answer `if:NrarrN` defined by
`f(n)={((n+1)/2,n is odd),(n/2,n is even):}`
View SolutionIn each of the following cases,state whether the function is onto,one to one or bijective.Justify your answer 'if:NrarrN defined by
f(n)={((n+1)/2,n is odd),(n/2,n is even):}`
View SolutionIn each of the following cases,state whether the function is onto,one to one or bijective.Justify your answer 'if:NrarrN defined by
f(n)={((n+1)/2,n is odd),(n/2,n is even):}`
View SolutionIn each of the following cases,state whether the function is onto,one to one or bijective.Justify your answer 'if:NrarrN defined by
f(n)={((n+1)/2,n is odd),(n/2,n is even):}`
View SolutionProve that the greatest integer function `f : R rarrR` given by `f(x) =[x]` is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
View SolutionLet R be a relation in the set N of natural numbers given by `R={(a,b):a=b-2}`. Choose the correct answer.a)`(2,3)inR` b)`(3,8)inR` c)`(6,8)inR` d)`(8,7)inR`
View SolutionLet `**` be a binary operation on the set Z of integers as `a**b=a+b+1`. Then find the identity element:
View SolutionLet `A=R-{3}` and `B=R-{1}` Consider the function `f:ArarrB` defined by `f(x)=frac(x-2)(x-3)`
Is `f` one-one and onto? Justify your answer.
View SolutionLet `A=R-{3}`and `B=R-{1}`consider the function `f:ArarrB` defined by `f(x)=(x-2)/(x-3)`.Is it invertible?Why?
View SolutionLet `A=R-{3}`and `B=R-{1}`consider the function `f:ArarrB` defined by `f(x)=(x-2)/(x-3)`.If invertible,find inverse of f(x).
View SolutionIf `f(x)=sinx,g(x)=x^2,x in R` , then find `(fog)(x)`
View SolutionLet u and v be two functions defined on R as `u(x)=2x-3` and `v(x)=(3+x)/2` .Prove that u and v are inverse to each other.
View SolutionThe function P is defined as "to each person on the earth is assigned a date of birth." is this a function one-one? Give reason.
View Solution
EXAMPLE questions and complete solutions for chapter RELATIONS AND FUNCTIONS of BODY BOOKS PUBLICATION of Class 12