Complete Solutions to EXAMPLE of chapter DIFFERENTIAL EQUATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | DIFFERENTIAL EQUATIONS |
| BODY BOOKS PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Consider `xdy/dx=y-xtan(y/x),` Express `dy/dx` as a function of y/x.
View SolutionConsider `xdy/dx=y-xtan(y/x),` Solve the equation using the substitution y=vx.
View SolutionObtain the equation of the family of straight lines parallel to the line y=2x.
View SolutionSolve the DE`dy/dx=2xy/(1+x^2)+x^2+2
View SolutionSolve the initial value problem:
`dy/dx=ytan2x`,`y(0)=2`
View SolutionFind the degree of the differential equation in `((d^2y)/dx^2)^2=(1+dy/dx)^(3//2)`.
View SolutionFind the integrating factor of the differential equation `cosx(dy//dx)+ysinx=1`.
View SolutionChoose the correct answer. The number of arbitrary constains in the general solution of a differential equation of fourth order is
View SolutionWhat is the degree of the following differential equation? `5x(dy/dx)^2-(d^2y)/dx^2-6y=logx`
View SolutionSolve `dy/dx=(x.e^xlogx+e^x)/(xcosy)`.
View Solution`(dy)/(dx)=(1-cos x)/(1+cos x)`
View Solution`e^x tan y d x+(1-e^x) (sec ^2 y) d y=0`
View SolutionSolve `(y+3x^2)dx/dy=x`
View SolutionConsider the differential equation `3e^xtan y dx-(1+e^x)sec^2 y dy=0` Order of the differential equation is ....
View SolutionConsider the differential equation `3e^xtan y dx-(1+e^x)sec^2 y dy=0` Express the differential equation in variable separable form.
View SolutionSolve the differential equation `3 e^x tan y d x-(1+e^x) (sec ^(2) y) d y=0`
View SolutionSolve `sqrt(a+x)dy/dx+x=0`
View SolutionSolve `dy/dx=e^(x-y)+x^2e^-y`
View SolutionGiven `y dx-xdy+(logx)dx=0` Express the given equation in the form `dy/dx+Py=Q`.
View SolutionGiven `y dx-xdy+(logx)dx=0` Find the integrating factor.
View SolutionGiven `y dx-xdy+(logx)dx=0` Solve the given differential equation.
View SolutionConsider the differential equation `dy/dx+ytanx=x^2cos^2x`. Find its integrating factor.
View SolutionConsider the differential equation `dy/dx+ytanx=x^2cos^2x`. Solve the differential equation.
View SolutionFind the solution of `e^xcosydx-e^xsinydy=0`.
View SolutionFind the order of the differential equation`((d^2y)/dx^2)^3=(1+dy/dx)^(1//2)`.
View SolutionShow that the function `y=Ax+B/x` is a solution of the differential equation `x^2(d^2y)/dx^2+xdy/dx-y=0`.
View SolutionForm the differential equation corresponding to `y^2=a(b-x)(b+x)` by eliminating a and b.
View SolutionFind the equation of a curve passing through the point `(-2,3)`, given that the slope of the tangent to the curve at any point `(x, y)` is `(2 x)/y^2`
View SolutionFind the differential equation of all the circles touching the x-axis at origin.
View SolutionForm a differential equation of the family
of circles having centre on y-axis and
radius 3 units.
View SolutionWrite the order and degree of the differential equation `((d^2s)/(dt^2))+3((ds)/(dt))^3+4=0`.
View SolutionSolve `dy/dx=1+x+y+xy`.
View SolutionSolve `dy/dx+y/x=logx`.
View SolutionA spherical rain drop evaporates at a rate proportional to its surface area. If its radius is originally 3 mm and after 1 hour i t is reduced to 2 mm, find an expression for radius of rain drop at any time.
View SolutionSolve `y'+y/x=x^3`.
View SolutionGiven `y dx-xdy+(logx)dx=0` Express the given equation in the form `dy/dx+Py=Q`.
View SolutionGiven `y dx-xdy+(logx)dx=0` Find the integrating factor.
View SolutionGiven `y dx-xdy+(logx)dx=0` Solve the given differential equation.
View SolutionWrite the equation of a circle having centre at (a,b) and radius 'r'.
View SolutionBy eliminating 'a' and 'b' from the equation of circle with center (a,b) and radius r. form the differential equation corresponding to the family.
View SolutionSolve : `(1+x^2)dy/dx+2xy-4x^2=0`.
View SolutionShow that the general solution of the differential equation `(dy)/(dx)+(y^2+y+1)/(x^2+x+1)=0` is given by `((x+y)+1)=A(1-x-y-2 x y)`, where `A` is parameter.
View SolutionShow that the differential equation x cos(y/x)`(dy)/(dx)` = y cos(y/x) + x is homogeneous and solve it.
View SolutionSolve `dy/dx+1=e^(x+y)`.
View SolutionSolve `dy/dx+ycotx=2cosx`.
View SolutionFind the equation of a curve passing through
the point (0,-2) given that at any point (x,y)
on the curve, the product of the slope of its
tangent and y coordinate of the point is equal
to the x coordinate of the point.
View SolutionSolve the initial value problem `y'=ycot2x`,`y(pi/4)=2`
View SolutionConsider the differential equation given
below.
`(d^4y)/dx^4-sin((d^3y)/dx^3)=0`
write the order and degree of the DE(if
defined)
View SolutionFind the Differential equation satisfying
the family of curves `y^2=a(b^2-x^2)`,a and b
are arbitrary constants.
View SolutionFind the Differential equation satisfying
the family of curves `y=ae^(3x)+be^(-2x)`,a
and b are arbitrary constants.
View SolutionChoose the correct answer from the
bracket.
The solution of the differential equation
`xdy+ydx=0` represents
View SolutionForm the DE of the family of circles
touching the x-axix at origin.
View SolutionFind a particular solution satisfying the
given condition.`(x^3+x^2+x+1)dy/dx=2x^2+x`
when `y=1`,`x=0`
View SolutionConsider the DE `xydy/dx=(x+2)(y+2)` Find the equation of the family of curves
View SolutionFor the DE `xydy/dx=(x+2)(y+2)`,find the
solution curve passing through the point (1,-1).
View SolutionConsider the differential equation `xdy-ydx=sqrt(x^2+y^2)dx` Find `dy/dx`
View SolutionConsider the differential equation `xdy-ydx=sqrt(x^2+y^2)dx` Solve the above differential equation.
View SolutionThe general solution of the DE
dy/dx= e^x-y is
View SolutionSolve the DE`dy/dx=2xy/(1+x^2)+x^2+2
View SolutionChoose the correct answer from the bracket determine the order and degree of the differential equation, `2x(d^4y)/dx^4+5x^2(dy/dx)^3-xy=0` a)Fourth order, first degree b)Third order, first degree c)first order, fourth degree d)first order, third degree
View SolutionThe population of a country doubles in 50 years. How many years will it be five times as much? Assume that the rate of increase is proportional to the number inhabitants. (hint: log2=0.6931, log5=1.6094)
View SolutionThe volume of spherical ballon being inflated at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of the balloon after t seconds.
View SolutionSolve the differential equation:`[xsin^2(y/x)-y]dx+x dy=0`.
View SolutionSolve the differential equation: `(xcos(y/x)+ysin(y/x))y-(ysin(y/x)-xcos(y/x))xdy/dx=0`.
View SolutionIf y=mx+c is a tangent to the circle `x^2+y^2=1`, show that `c=+-sqrt(1+m^2)`
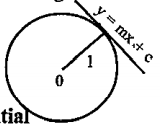
View SolutionFind the differential equation of all straight lines touching the circle `x^2+y^2=1`.
View SolutionGiven `(1+e^(x//y))dx+e^(x//y)(1-x/y)dy=0` Express the differential equation as `dx/dy`= A function of `(x/y)`.
View SolutionGiven `(1+e^(x//y))dx+e^(x//y)(1-x/y)dy=0` Solve the differential equation using x=vy.
View SolutionConsider `(1+y^2)dx=(tan^-1y-x)dy` Express the equation in the form `dx/dy+Px=Q`
View SolutionConsider `(1+y^2)dx=(tan^-1y-x)dy` Find the integrating factor.
View SolutionConsider `(1+y^2)dx=(tan^-1y-x)dy` Solve the given equation.
View SolutionConsider `dy/dx=-(2xy)/(x^2+1)` Find the general solution of the differential equation.
View SolutionConsider `dy/dx=-(2xy)/(x^2+1)` Find the equation of the curve that passes through (1,2) and satisfies the differential equation.
View SolutionExpress the differential equation `(x^2+1)dy/dx+2xy=sqrt(x^2+4)` in the form `dy/dx+P(x)y=q(x)`.
View Solution`(x^2+1)dy/dx+2xy=sqrt(x^2+4)` Find its integrating factor.
View Solution`(x^2+1)dy/dx+2xy=sqrt(x^2+4)` Obtain the general solution.
View SolutionConsider the differential equation `x(d^2y)/dx^2+2dy/dx-xy+x^2-2=0`. Write the order and degree.
View SolutionConsider the differential equation `x(d^2y)/dx^2+2dy/dx-xy+x^2-2=0`.Show that `xy=ae^x+be^-x+x^2` is a solution of the given equation.
View SolutionConsider the differential equation `(x^2-y^2)dx+2xydy=0`. Write the order and degree of differential equation.
View SolutionConsider the differential equation `(x^2-y^2)dx+2xydy=0`. Show that the differential equation is homogeneous.
View Solutionsolve the differential equation `(x^2-y^2) d x+2 x y d y=0`
View SolutionConsider the differential equation `(x^2-y^2)dx+2xydy=0`. Choose the correct solution from the following. For y=1 when x=1 a)`x^2+y^2=-2x` b)`x^2+y^2=2x` c)`x^2+y^2-x=0` d)`x^2+y^2+x=0`
View SolutionConsider `xlogxdy/dx+y=2/xlogx`,`x>0` Express the equation in the form `dy/dx+Py=Q`.
View SolutionConsider `xlogxdy/dx+y=2/xlogx`,`x>0` Find the integrating factor.
View SolutionConsider `xlogxdy/dx+y=2/xlogx`,`x>0` Solve the differential equation.
View SolutionThe general solution of a differential equation contains 3 arbitrary constants. Then what is the order of the differential equation?A)2 B)3 C)0 D)1
View SolutionCheck whether `y=e^(-3x)` is a solution of the differential equation `frac(d^2y)(dx^2)+frac(dy)(dx)-6y=0`
View SolutionForm the differential equation corresponding to the curve `y=mx`
View SolutionConsider the D.E `dy/dx+y/x=x^2`
Solve the D.E.
View SolutionThe order of the differential equation formed by `y=Asinx+Bcosx` , where A and B are arbitary constants is ... a)1 b)2 c)0 d)3
View SolutionSolve the differential equation `sec^2xtanydx+sec^2ytanxdy=0`
View SolutionConsider the Differential equation
`cos^2xdy/dx+y=tanx` . Find
its degree
View SolutionConsider the Differential equation `cos^2xdy/dx+y=tanx` . Find the integrating factor
View SolutionConsider the Differential equation `cos^2xdy/dx+y=tanx` . Find the general solution.
View SolutionFind the general solution of the differential equation
`xdy/dx+2y=x^2 log x`
View SolutionThe degree of the differential equation
`xy((d^2y)/dx^2)^2+x^4(dy/dx)^3-ydy/dx=0` is
View SolutionFind the general solution of the differential equation
`sec^2xtan ydx +sec^2 y tan xdy=0`
View SolutionThe order of the differential equation `x^2 (d^2y)/(dx^2)=1+(dy/dx)^3` is
View SolutionFind the particular solution of the
differential equation
`(1+x^2)(dy)/(dx)+2xy=1/(1+x^2)`,when `y=0`,
`x=1`.
View Solution`y=acosx+bsinx` is the solution of the
differential equation
`(d^2y)/(dx^2)+y=0`
View Solution
EXAMPLE questions and complete solutions for chapter DIFFERENTIAL EQUATIONS of BODY BOOKS PUBLICATION of Class 12