Complete Solutions to EXAMPLE of chapter VECTOR ALGEBRA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | VECTOR ALGEBRA |
| BODY BOOKS PUBLICATION | EXAMPLE |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
Prove that `(veca xx vecb)^2=|(veca.veca,veca.vecb),(veca.vecb,vecb.vecb)|`.
View SolutionUsing vectors,prove that angle in a semi circle is a right angle.
View SolutionFind a vector of magnitute 12 units perpendicular to the containing the vectors`4hati+6hatj-hatk and 3hati+8hatj+hatk`.
View SolutionShow that the area of the parallelogram having diagonals `3hati+hatj-2hatk and hati-3hatj+4hatk` is `5sqrt3`
View SolutionFind the values of x for which the angle between the vectors`veca=2xhati+4xhatj+hatk` and `vecb=7xhati-2hatj+xhatk` is obtuse.
View SolutionIf A(1,2,4) and B(2,-1,3) are two points (i)Find `vec(AB)`
View SolutionIf A(1,2,4) and B(2,-1,3) are two points (ii) Find unit vector along `vec(AB)
View SolutionShow that the points with position vectors `2hati+6hatj+3hatk,hati+2hatj+7hatk and 3hati+10hatj-hatk` are collinear.
View SolutionLet the vectors 'veca, vecb, vecc' be given as 'a_1 hati+a_2 hatj+a_3 hatk, b_1 hati+b_2 hatj+b_3 hatk, c_1 hati+c_2 hatj+c_3 hatk', Then show that 'veca xx(vecb+vecc)=veca xx vecb+veca xx vecc'
View SolutionConsider a cube of side 'a' unit has one vertex at the origin O.
Show that the angle between the main diagonals of the above cube is `cos^-1(1/3)`

View Solution`veca,vecb,vecc` are three non zero vectors such that ` vecaxxvecb=vecc,vecbxxvecc=veca`.Prove that `veca,vecb,vecc` are mutually at right angle and `|vecb|=1,|vecc|=|veca|`.
View SolutionFind `|vecaxxvecb|`,If `veca=2hati-hatj+3hatk` and `vecb=hati+2hatj-hatk`
View SolutionChoose the correct answer from the bracket.The angle between the vectors `veca and vecb` with magnitude 1 and 2 respectively having `veca.vecb=sqrt3` a)`pi/3` b)`pi/4` c)`pi/6` d)`pi/2`
View SolutionIf the vectors `veca=hati+hatj+hatk,vecb=2hati-hatj+hatk and vecc=khati-2hatj+3hatk` are coplaner then find the value of k.
View SolutionWrite two different vectors having same magnitude.
View SolutionFind the direction cosines of the vector `2hati+hatj+3hatk`
View SolutionConsider two points A and B with position vectors `vec(OA)=veca-4vecb` and `vec(OB)=veca-vecb`.Find the position vector of a point R which divides the line joining A and B in the ratio 2:1 internally
View SolutionFind a unit vector perpedicular to each of the vector `veca+vecb` and `veca-vecb` where `veca=2hati+hatj+hatk and vecb=hati-hatj+hatk`
View SolutionChoose the correct answer from the backet. If a unit vector `hata` makes angles `pi/4` with i and `pi/3` with j and acute angle `theta` with k.
then `theta` is
View SolutionFind a unit vector `hata`.
View SolutionWrite down a unit vector in XY plane, making an angle of `60°` with the positive direction of x-axis.
View SolutionIf `veca,vecb,vecc` are three coplanar vectors, then `[vecavecbvecc]` is
View SolutionFind P,if `veca=-2hati-hatj+2hatk and vecb=hati+phatj+hatk` and`vecaxxvecb=3hati+4hatj+5hatk`.
View Solution`vecaxxveca`is equal to ……
View SolutionFind the area of a triangle with vertices A(2,3,1),B(1,1,2) and C(1,2,1).
View SolutionConsider the points A(0,-2,1),B(1,-1,-2) and C(-1,1,0) lyind in the plane. Compute `vec(AB) and ` `vec(AC)``.
View SolutionConsider the points A(0,-2,1),B(1,-1,-2) and C(-1,1,0) lyind in the plane. Find `vec(AB)xxvec(AC)`
View SolutionLet `veca=7hati-2hatj+hatk,vecb=hati-2hatj+2hatk and vecc=3hati-8hatk`.i Compute `vecaxxvecb` and` vecaxxvecc`.
View SolutionLet `veca=7hati-2hatj+hatk,vecb=hati-2hatj+2hatk and vecc=3hati-8hatk`.ii Are the products `veca.(vecbxxvecc)` and `(vecaxxvecb).vecc` obtained are same?
View SolutionLet `veca=7hati-2hatj+hatk,vecb=hati-2hatj+2hatk and vecc=3hati-8hatk` and `vecd=-hatj+hatk`.(i) Find `vecb-veca`
View SolutionLet `veca=7hati-2hatj+hatk,vecb=hati-2hatj+2hatk and vecc=3hati-8hatk` and`vecd=-hatj+hatk`.(iii)Find the unit vector along `vecb-veca`
View SolutionGiven the position vectors of three points `A(hati-hatj+2hatk ),B(4hati+5hatj+8hatk) and C(3hati+3hatj+6hatk)`. Find the projection of `vec(AB) on vec(AC)`.
View SolutionGiven the position vectors of three points `A(hati-hatj+2hatk ),B(4hati+5hatj+8hatk) and C(3hati+3hatj+6hatk)` . Prove that A,B and C are collinear.
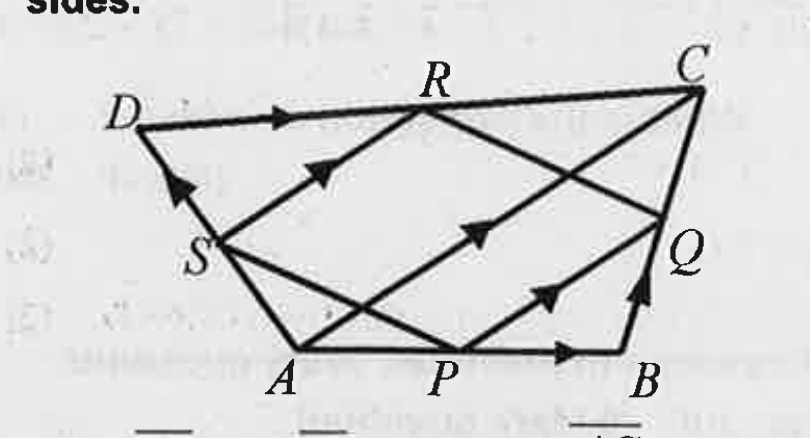
View SolutionConsider the following quadrilateral ABCD in which P,Q,R,S are the mid points of the sides.
If `veca` is any vector, prove that `veca=(veca*i)i+(veca*j)j+(veca*k)k`.
View SolutionIf `veca` and `vecb` are unit vectors inclined at an angle `theta`,then prove that `sin(theta/2)=1/2|veca-vecb| `
View SolutionIf `veca=xhati+2hatj-zhatk and vecb=3hati-yhatj+hatk` are two equal vectors then write the value of x+y+z.
View SolutionIf `veca,vecb,vecc` are three vectors such that `|veca|=5,|vecb|=12 and |vecc|=13` and`veca+vecb+vecc=vec0`,find the value of `veca.vecb+vecb.vecc+vecc.veca`.
View SolutionIf `i+j+k,2i+5j,3i+2j-3k,i-6j-k` respectively are the position vector of points A,B,C and D. Then find the angle between the vectors `vec(AB)` and `vec(CD)`.
View SolutionIf `i+j+k,2i+5j,3i+2j-3k,i-6j-k` respectively are the position vector of points A,B,C and D. Then
Deduce that `vec(AB)` parallel to `vec(CD)`.
View SolutionFind the area of the parallelogram whose adjacent are determined by the vectors`veca=overset^^i-overset^^j+3overset^^k "and"vecb=2overset^^i-7overset^^j+overset^^k` .
View SolutionIf 'veca.veca=0' and 'veca. vecb=0', then what can be concluded about the vector 'vecb' ?
View SolutionLet the vectors`veca"and"vecb`be such that
`|veca|=3"and"|vecb|=sqrt2/3`,then `vecaxxvecb ` is a unit vector, if the angle between `veca"and"vecb`is : a)`pi/6` b)`pi/4` c)`pi/3` d)`pi/2`
View SolutionFind a unit vector perpendicular to the plane ABC where A,B,C are point (1,1,2),(2,3,5) and (1,5,5).
View SolutionThe Cartesian equation of two lines are
`(x+1)/7=(y+1)/-6=(z+1)/1` and `(x-3)/1=(y-5)/-2=(z-7)/1` .Write the vector equations.
View SolutionIf `veca,vecb,vecc` are three coplanar vectors, then `[vecavecbvecc]` is
View SolutionIf `absveca=2`,`absvecb=3` and `theta` is the angle between `veca` and `vecb`. Then the maximum value of `veca.vecb` occurs when` theta`=.....a)`pi/2` b)`pi` c)0 d)`pi/4`
View SolutionIf `vecb=2hati+hatj-hatk`,`vecc=hati+3hatk` and `veca` is a unit vector. Find the maximum value of scalar triple product `[veca vecb vecc]`
View SolutionThe position vectors of three points A,B,C are given to be `i+3j+3k` , `4i+4k`, `-2i+4j+2k` respectively.Find the angle between `vec(AB)` and `vec(AC)`
View SolutionThe position vectors of three points A,B,C are given to be `i+3j+3k` , `4i+4k`, `(-2i+4j+2k` respectively
Find a vector which is perpendicular to both `vec(AB)` and `vec(AC)` having magnitude 9 units.
View SolutionIf `bara,barb,barc` are coplaner vectors , write the vector perpendicular to `bara`
View SolutionIf `veca,vecb,vecc`are coplanar,prove that `veca+vecb,vecb+vecc,vecc+veca`are coplanar.
View SolutionProve that `[ veca+vecb vecb+vecc vecc+veca]=2[veca vecb vecc]`
View SolutionShow that if `veca+vecb,vecb+vecc,vecc+veca` are coplanar then `veca,vecb,vecc` are also coplanar.
View SolutionIf `veca=3hati+2hatj+2hatk,vecb=hati+2hatj-2hatk` Find `veca+vecb` and `veca-vecb`
View SolutionIf `veca=3hati+2hatj+2hatk,vecb=hati+2hatj-2hatk`. Find a unit vector perpendicular to both `veca+vecb` and `veca-vecb`
View SolutionConsider the points A(1.2.7),B(2,6,3),C(3,10,-1)
find `bar(AB),bar(BC)`
View Solution
EXAMPLE questions and complete solutions for chapter VECTOR ALGEBRA of BODY BOOKS PUBLICATION of Class 12