Complete Solutions to EXAMPLE of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| BODY BOOKS PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A coin is tossed 6 times,What is the probability of getting exactly 4 heads.
View SolutionFind the probability of obtaining an even prime number as the sum when a pair of dice are rolled.
View SolutionIn an examination.30% of students failed in Maths,20% of students failed in Chemistry and 10% of students failed in both Maths & Chemistry.A student is selected at random.Find the probability that (i) The student has failed in Maths.
View SolutionIn an examination.30% of students failed in Maths,20% of students failed in Chemistry and 10% of students failed in both Maths & Chemistry.A student is selected at random.Find the probability that (ii) The student has failed in Chemistry
View SolutionIn an examination.30% of students failed in Maths,20% of students failed in Chemistry and 10% of students failed in both Maths & Chemistry.A student is selected at random.Find the probability that the student has failed in Maths,it is known that he has failed in Chemistry.
View SolutionA die is thrown and six possible out comes are equally liked.E is the event,the number appearing is a an multiple of 3,and F is the event,'The number appearing is even',Calculate P(E) and P(F)
View SolutionA die is thrown and six possible outcomes are equally liked.E is the event,the number appearing is a an multiple of 3,and F is the event,'The number appearing is even',Calculate `P(EcapF)`
View SolutionA die thrown.If E is the event 'the number appearing is a multiple of 3' and F be the event 'the number appearing is even' then find whether E and F are independent ?
View SolutionFind the probability distribution of the number of sucesses in two tosses of a die where success is defined as
number greater than 4
View SolutionFind the bionomial distribution whose mean is 10 and standard deviation `2sqrt2`
View SolutionA bag 'X'contains 2 white and 3 red balls and a bag Y contains 4 white and 5 red balls.One ball is drawn at random from one of the bags and is found to be red.Find the probability that it was drawn from bag Y.
View Solution5 boys and 5 girls are siting in a row randomly . The probability that boys and girls sit alternatively is : a)`(5)/(126)` b)` (1)/(126)` c)` ( 4)/(126)` d)` (6)/(126)`
View SolutionIf `P(A)=3/4`,P(B)=4/5` and ``P(A uu B)=31/20`` the events A and B are
View SolutionWhat is the probability that the position in which the consonants remains unchanged when the letters of "MATH"are re-arranged?
View SolutionA shooter can hit a target once in a 4 shots.If he fires 4 shots in succession,what is the probability that he will hit his target.
View SolutionTwo balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that one of them is black and the other is red.
View SolutionOut of 9 outstanding students of a school,there are 4 boys and 5 girls.A team of 4 students is to be selected for a quiz competition.Find the probability that 2 boys and 2 girls are selected.
View SolutionIn a binominal distribution mean is 6 and standard deviation is `sqrt2`.What is the number of trials.
View SolutionA company has two plants to manufacture scooters.Plant I manufactures 70% of the scooters and Plant II manufactures 30%.At Plant I,30% of the scooters are of standard quality and at Plant II,90% of the scooters are rated as of standard quality.A scooter is chosen at random and is found to be of standard quality.What is the probability that it has come from Plant II?
View SolutionLet E and F be events such that `P(E)=1/3,P(F)=1/4,P(EcapF)=1/5`.Find `P(E|F)`
View SolutionLet E and F be events such that `P(E)=1/3,P(F)=1/4,P(EcapF)=1/5`Find`P(F|E)`
View SolutionLet E and F be events such that `P(E)=1/3,P(F)=1/4,P(EcapF)=1/5`Find`P(EcupF)`
View SolutionLet E and F be events such that `P(E)=1/3,P(F)=1/4,P(EcapF)=1/5`Find `P(barF\\barE)`
View SolutionA bag contains 4 white and 2 black balls.Another bag contains 3 white and 5 black balls.If one ball is drawn from each bag.Find the probability that both are white
View SolutionA bag contains 4 white and 2 black balls.Another bag contains 3 white and 5 black balls.If one ball is drawn from each bag.Find the probability that both are black
View SolutionA bag contains 4 white and 2 black balls.Another bag contains 3 white and 5 black balls.If one ball is drawn from each bag.Find the probability that One is white and one is black.
View SolutionIt is known that `10%` of certain articles manufactured are defective . What is the probability that in a random sample of 12 such articles 9 are defective?
View SolutionA can hit target 4 times out of 5 times,B can hit target 3 times out of 4 times and C can hit target 2 times out of 3 times. They fire simultaneously.Find the Probability Any two out of A,B and C will hit the target.
View SolutionA can hit target 4 times out of 5 times,B can hit target 3 times out of 4 times and C can hit target 2 times out of 3 times. They fire simultaneously.Find the Probability that None of them will hit the target.
View SolutionA coin is tossed 5 times.What is the probability of getting 3 heads?
View SolutionA coin is tossed 5 times What is the probability of getting at least 3 heads?
View SolutionAssume that each born child is equally likely to be a boy or a girl. If a family has two children,what is the conditional probability that both are girls given that
the youngest is a girl
View SolutionA coin is tossed so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, Find the probability distribution of number of tails.
View SolutionAssume that each born child is equally likely to be a boy or a girl. If a family has two children,what is the conditional probability that both are girls given that
atleast one is a girl
View SolutionA and B independently try to solve a problem.Probability that A slove the problem is 1/3 and that B solves the problem is 1/4.Find the probability that both of them solves the problem.
View SolutionA and B independently try to solve a problem.Probability that A slove the problem is 1/3 and that B solves the problem is 1/4.Find the probability that the problem is solved
View SolutionFind the probability distribution of the number of heads in three tosses of a fair coin.
View SolutionWhat is meant by mutually exclusive events?
View SolutionFind the probability of drawing a one-rupee coin from a purse with two compartments, one of which contains 3 fifty-paise and 2 one-rupee coins,and the other 2 fifty paise and 3 one-rupee coins.
View SolutionIn four throws with a pair of dice,what is the probability of throwing doublets twice
View SolutionIn four throws with a pair of dice,what is the probability of throwing doublets at least twice.
View SolutionSuppose that 5 men out of 100 and 25 women out of thousand are colour blind.A colour blind person is chosen at random.What is the probability of this being male (assuming that males and females are in equal proportion).
View SolutionA can hit a target 4 times in 5 shots.B three times in 4 shots,C two times in three shots.Calculate the probability that A,B,C all may hit.
View SolutionA can hit a target 4 times in 5 shots.B three times in 4 shots,C two times in three shots.Calculate the probability that B,C may hit and A may lose.
View SolutionA can hit a target 4 times in 5 shots.B three times in 4 shots,C two times in three shots.Calculate the probability that any two will hit the target.
View SolutionA can hit target 4 times out of 5 times,B can hit target 3 times out of 4 times and C can hit target 2 times out of 3 times. They fire simultaneously.Find the Probability that None of them will hit the target.
View SolutionAn urn contains 5 white and 8 black balls.Two successive draws
of three balls at a time are made such that the balls are not
replaced brfore the second trial.Find the probability in ecah
case that the first drawing will give 3 white and the
second 3 black balls.
View SolutionAn urn contains 5 white and 8 black balls.Two successive draws
of three balls at a time are made such that the balls are not
replaced brfore the second trial.Find the probability in ecah
case that the first drawing will give 3 white and the
second 3 black balls.
View SolutionTwo persons A and B throw a die alternatively till one of them gets a three and wins the game.If A begins,find (i) the probability of winning of A.
View SolutionTwo persons A and B throw a die alternatively till one of them gets a three and wins the game.If A begins,find (ii) the probability of winning of B.
View SolutionA doctor claims that 60% of the patients he examines are allergic to some type of weed.what is the probability that (i) Exactly three of his next four patients are allergic to weeds.
View SolutionA doctor claims that 60% of the patients he examines are allergic to some type of weed.what is the probability that (ii)None of his next four patients is allergic to weeds.
View SolutionProbability that a problem will be solved by three students are 1/4,1/2,3/4 respectively.what is the probability that all solves the problem.
View SolutionProbability that a problem will be solved by three students are 1/4,1/2,3/4 respectively.what is the probability that none solves the problem
View SolutionProbability that a problem will be solved by three students are 1/4,1/2,3/4 respectively.what is the probability that the problem will be solved
View SolutionProbability that a problem will be solved by three students are 1/4,1/2,3/4 respectively.what is the probability that (iv).Exactly one solves the problem
View SolutionA coin is tossed three times,where the events A:occurring at most two heads,B:occuring at most one tail (i)Write P(A),P(B)
View SolutionA coin is tossed three times,where the events A:occurring at most two heads,B:occuring at most one tail (ii)Find `P(A|B)`and `P(B|A)`
View SolutionIn a hostel 50% of the girls like tea, 40% like coffee and 20% like both tea and coffee
A girl is selected at random.
Find the probability that she likes neither tea or coffee .
View SolutionIn a hostel 50% of the girls like tea, 40% like coffee and 20% like both tea and coffee.A girl is selected at random.If the girl likes tea,then find the probability that she likes coffee.
View SolutionIn a hostel 50% of the girls like tea, 40% like coffee and 20% like both tea and coffee .A girl is selected at random.If she likes coffee then find the probability she likes tea.
View SolutionVineetha and Reshma are competing for the post of school leader. The probability Vineetha to be elected is 0.6 and that of Reshma is 0.4 Futher if Vineetha is elected the probability of introducing a new pattern of election is 0.7 and the corresponding probability is 0.3 , if reshma is elected. Find the probability that the new pattern of election is introduced by Reshma ?
View SolutionFind the probability distribution of the number of success in two tosses of a die where the success is defined as getting a number less than 5.
View SolutionGiven that E and F are events such that P(E) =0.6 P(F)=0.4 and `P(EcapF)=0.2`Then `(P(E|F))/(P(F|E))`is (1/2,1/3,3/2,2/3)
View SolutionA die thrown twice and the sum of the numbers appearing is observed to be greater than 9.What is the conditional probability that the number 5 is appearing at least once.
View SolutionA and B are two events such that P(A)=1/5 and`P(AcupB)=2/3`.Find p(B) if they are mutually exclusive a)1/5 b) 2/5 c) 3/5 d) 7/15
View SolutionA box contains 3 red and 4 blue balls. Two balls are drawn one by one without replacement. Find the probability of getting both balls red.
View SolutionThree cards are drawn successively without replacement from a pack of 52 cards. What is the probability that first two cards are queen and the third is king.
View SolutionFind `P(AnnB)` If A and B are independent events with P(A)=`1/5` and P(B)=`5/8`. a)`6/13` b)`33/40` c)`1/8` d)`5/8`
View SolutionAn unbiased die is thrown twice. Let the event A be getting prime number in the first throw and B be the event of getting an even number in the second throw. Check the independence of the events A and B
View SolutionThe probability of solving a problem independently by A and B are `1/3` and `1/4` respectively. Find the probability that exactly one of them solves the problem.
View SolutionA set of events
`E_1,E_2,.........E_n`
are said to be a partition of the sample space, then which of the following conditions is always not true
View SolutionA person has undertaken a business. The probabilities are 0.80 that there will be a crisis, 0.85 that the business will be completed on time if there is no crisis and 0.35 that the business will be completed on time if there is a crisis. Determine the probability that the business will be complete on time
View SolutionA box contains 5 red and 10 black balls. A ball is drawn at random, its colour is noted and is returned to the box. More over 2 additional balls of the colour drawn are put in the box and then a ball is drawn.what is the probability that the second ball is red.
View SolutionBag 1 contains 5 red and 6 black balls. Bag2 contains 7 red and 5 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it was drawn from bag 1.
View SolutionA card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being diamond.
View SolutionIf X denotes number of heads obtained in tossing two coins. Then which of the following is false a) X(HH) = 2 b)X(HT) = 1 c)X(TH) = 0 d)X(TT) = 0
View SolutionFind the probability distribution of number of heads in two tosses of a coin.
View SolutionA coin is tossed so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, Find the probability distribution of number of tails.
View SolutionFill in the blank of a probability distribution of a random variable X.
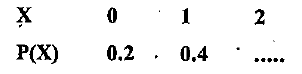
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionThe probability that a student is not a sportsman is 1/5.Then the
probability that out of 6 students,4 are sportsman is.
View SolutionFind the probability of throwing at most 2 sixes in 6 throws of a single die.
View SolutionOn a multiple choice examination with three possible answers for each of the five questions what is the probability that a candidate would get four or more correct answers just by guessing?
View SolutionIf P(A) = 0.8, P(B) = 0.5, P(B/A) = 0.4, Find
`P(AnnB)`
View SolutionIf P(A) = 0.8, P(B) = 0.5, P(B/A) = 0.4, Find
P(A/B)
View SolutionIf P(A) = 0.8, P(B) = 0.5, P(B|A) = 0.4, Find `P(AuuB)`
View SolutionTwo cards are drawn without replacement from a well shuffied pack
of 52 cards .Find the probability that one is a spade and other is
a queen of red colour.
View SolutionFind the probability distribution of number of heads in two tosses of a coin.
View SolutionAn experiments succeeds twice as often as it fails.Find the probability
that in the next six trials,there will be atleast 4 successes.
View SolutionA die is thrown again and again until three sixes are obtainined.find the probability of obtaining the third six in the sixth throw of the die.
View SolutionAn electronic assembly consists of two sub systems,say A and B.From previous testing procedures,the following probabilities are assumed to be Known.P(A fails)=0.2 P(B fails alone)=0.15 P(A and B fail)=0.15 Evaluate the following probabilities (i)P(A fails |B has failed)
View SolutionAn electronic assembly consists of two sub systems,say A and B.From previous testing procedures,the following probabilities are assumed to be Known.P(A fails)=0.2 P(B failsalone)=0.15 P(A and B fail)=0.15 Evaluate the following probabilities (ii)P (A fails alone)
View SolutionGiven two independent events `A` and `B` such that `P(A)=0.3, P(B)=0.6`. Find i) P(`A` and `B`) ii) P(`A` and not `B`) III) P(`A` or `B`) iv) P(neither `A` nor `B` )
View SolutionGiven two independent events `A` and `B` such that `P(A)=0.3, P(B)=0.6`. Find i) P(`A` and `B`) ii) P(`A` and not `B`) III) P(`A` or `B`) iv) P(neither `A` nor `B` )
View SolutionGiven two independent events `A` and `B` such that `P(A)=0.3, P(B)=0.6`. Find i) P(`A` and `B`) ii) P(`A` and not `B`) III) P(`A` or `B`) iv) P(neither `A` nor `B` )
View SolutionGiven two independent events A and B such that `P(A)=0.3,`P(B)=0.6`. find P(neither A nor B)
View SolutionThe probability distribution of a random variable X is given in the following table:
Find k.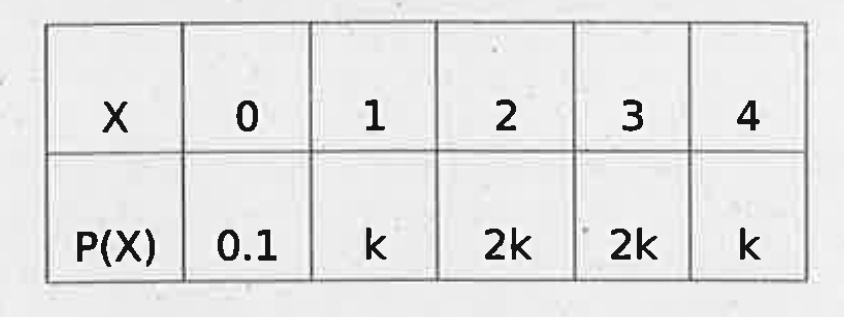
View SolutionThe probability distribution of a random variable X is
given in the following table: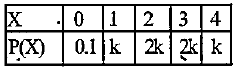
Find the probability that X lies between 1 and 4.
View SolutionThe probability distribution of a random variable X in given in the following table:
Find the mean of X.
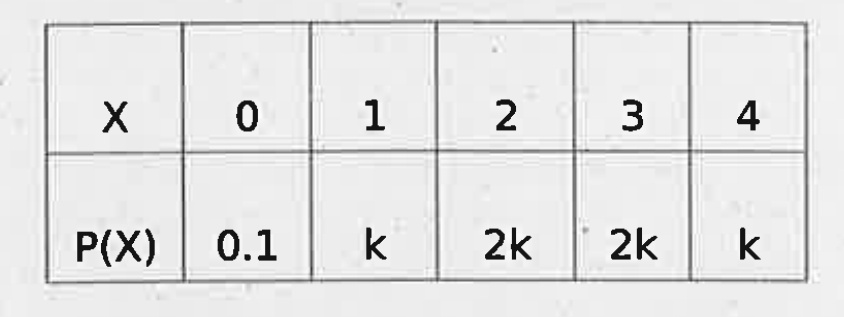
View Solution
EXAMPLE questions and complete solutions for chapter PROBABILITY of BODY BOOKS PUBLICATION of Class 12