Complete Solutions to EXERCISE of chapter QUESTION PAPER 2020 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | QUESTION PAPER 2020 |
| BODY BOOKS PUBLICATION | EXERCISE |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
Let R be a relation in the set N of natural numbers given by `R={(a,b):a=b-2}`. Choose the correct answer.a)`(2,3)inR` b)`(3,8)inR` c)`(6,8)inR` d)`(8,7)inR`
View SolutionLet `**` be a binary operation on the set Z of integers as `a**b=a+b+1`. Then find the identity element:
View SolutionWrite two non-zero matrices A and B for which `AB=0`.
View SolutionExpress `A=[(1,-1),(2,3)]` as the sum of a symmetric matrix and a skew symmetric matrix.
View Solutionusing properties of determinants, prove that `abs[[1,a,a^2],[1,b,b^2],[1,c,c^2]]=(a-b)(b-c)(c-a)`.
View SolutionWhich among the following is not true
View SolutionFind `dy/dx`, if `x^2+y^2+xy=100`
View SolutionIdentify the following function
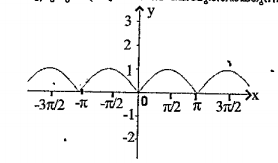
View SolutionIdentify the following function:
Is the function differentiable? Why?
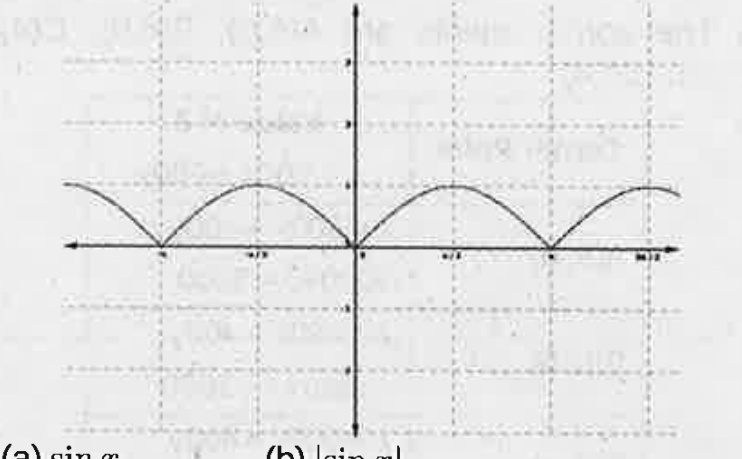
View SolutionFind derivative of `y=sqrttanx`
View SolutionThe slope of the tangent to the curve `y=e^(2x)` at (0,1) is.....a)1 b)2 c)0 d)-1
View SolutionFind the equation of a line perpendicular to the tangent to the curve `y=e^(2x)` at (0,1)) and passing through (2,3).
View SolutionThe general solution of a differential equation contains 3 arbitrary constants. Then what is the order of the differential equation?A)2 B)3 C)0 D)1
View SolutionCheck whether `y=e^(-3x)` is a solution of the differential equation `frac(d^2y)(dx^2)+frac(dy)(dx)-6y=0`
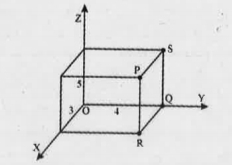
View SolutionConsider the following figure:
Find the distance of PQ.
View SolutionLet `A=R-{3}` and `B=R-{1}` consider the function `f:AtoB` defined by `f(x)=frac(x-2)(x-3)`. Is f one-one and onto? Justify your answer.
View SolutionLet `A=R-{3}`and `B=R-{1}`consider the function `f:ArarrB` defined by `f(x)=(x-2)/(x-3)`.Is it invertible?Why?
View SolutionLet `A=R-{3}`and `B=R-{1}`consider the function `f:ArarrB` defined by `f(x)=(x-2)/(x-3)`.If invertible,find inverse of f(x).
View SolutionIf `xy<1,tan^-1x+tan^-1y`=........ a)`tan^-1(frac(x-y)(1+xy))`
b)`tan^-1(frac(x+y)(1-xy))` c)`(tanx+tany)/(1-tanxtany)` d)`(tanx-tany)/(1-tanxtany)`
View SolutionSolve `tan^-1 2x+tan^-1 3x=pi/4`
View SolutionFind `dy/dx` if `y=x^x+x^sinx`.
View Solutionif `y=xcosx`, find `frac(d^2y)(dx^2)`
View Solution`intfracf(x)(tanx)dx=logabstanx+c`, then `f(x)` is
View SolutionIf `d/(d x) f(x)=4 x^3-3/x^4` such that `f(2)=0`, then `f(x)` is a)`x^4+1/x^3-(129)/8` b)`x^3+1/x^4 + (129)/8` c)`x^4+1/x^3+(129)/8` d)`x^3+1/x^4-(129)/8`
View SolutionThe area bounded by the curve y=f(x), x-axis and the line x=a and x=b is ?
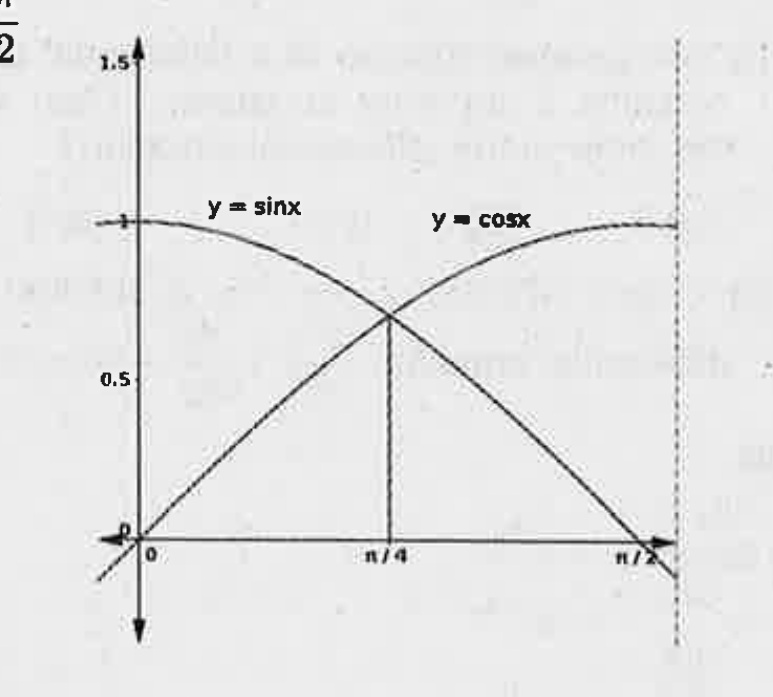
View SolutionFrom the following figure, find the area of the region bounded by the curves `y=sinx`, `y=cosx` and x axis as x varies from 0 to `pi/2`
View SolutionForm the differential equation corresponding to the curve `y=mx`
View SolutionConsider the D.E `dy/dx+y/x=x^2`
Solve the D.E.
View SolutionFind a unit vector perpendicular to the plane ABC where A,B,C are point (1,1,2),(2,3,5) and (1,5,5).
View SolutionThe Cartesian equation of two lines are
`(x+1)/7=(y+1)/-6=(z+1)/1` and `(x-3)/1=(y-5)/-2=(z-7)/1` .Write the vector equations.
View SolutionFind the shortest distance between the lines `(x+1)/7=(y+1)/-6=(z+1)/1` and `(x-3)/1=(y-5)/-2=(z-7)/1`
View SolutionIf a plane intersects the co-ordinate axes at a,b,c respectively,write the equation of the plane.
View SolutionFind the vector and cartesian equations of the plane that passes through
the point (1, 0, -2) and normal to the plane is `hati+hatj-hatk`
View SolutionLet two independent events A and B such that P(A)=0.3,P(B)=0.6.Find
P(A and B)
View SolutionLet two independent events A and B such that P(A)=0.3,P(B)=0.6
Find P(A and not B)
View SolutionLet two independent events A and B such that P(A)=0.3,P(B)=0.6
Find P(A or B)
View SolutionGiven two independent events A and B such that `P(A)=0.3,`P(B)=0.6`. find P(neither A nor B)
View SolutionLet `A=[a_(ij)]_(2times3)` where `a_(ij=i+j`. construct A.
View SolutionLet `A=[a_(ij)]_(2times3)` where `a_(ij=i+j`. construct A.Find AA' and hence prove that AA' is symmetric.
View SolutionFor any square matrix A,prove that `A+A' is symmetric.
View SolutionIf A is a skew symmetric matrix of order 3. Then prove that it's determinant is zero. (without using examples).
View SolutionGiven `abs [[2+x,3,4],[1,-1,2],[x,1,5]]` is a singular matrix. Find the value of x
View SolutionGiven A and B are square matrices of order 2 such that `absA=-1`, `absB=3`. Find `abs(3AB)`.
View SolutionFind the intervals in which the function `f(x)=x^2+2x-5` strictly increasing or decreasing.
View SolutionFind the equation of tangents and normals to the given curves `y=x^3` at `(1,1)`
View SolutionFind local maximum and local minimum if any for the function. `h(x)=sinx+cosx.``0 lt x lt (pi/2)`
View SolutionIntegrate the following
`intfrac(dx)(1+x^2/4)`
View SolutionIntegrate the following
`intfrac(x)((x-1)(x-2))dx`
View SolutionIntegrate the following `int_0^fracpi2xcosxdx`
View SolutionIf `veca,vecb,vecc` are three coplanar vectors, then `[vecavecbvecc]` is
View SolutionIf `absveca=2`,`absvecb=3` and `theta` is the angle between `veca` and `vecb`. Then the maximum value of `veca.vecb` occurs when` theta`=.....a)`pi/2` b)`pi` c)0 d)`pi/4`
View SolutionIf `vecb=2hati+hatj-hatk`,`vecc=hati+3hatk` and `veca` is a unit vector. Find the maximum value of scalar triple product `[veca vecb vecc]`
View SolutionSolve the linear programming problem graphically:
Max: `z=3x+2y`
Subject to:
`x+2yle10,3x+yle15,xge0,yge0`
View SolutionThe probability distribution of a random variable X is given in the following table:
Find k.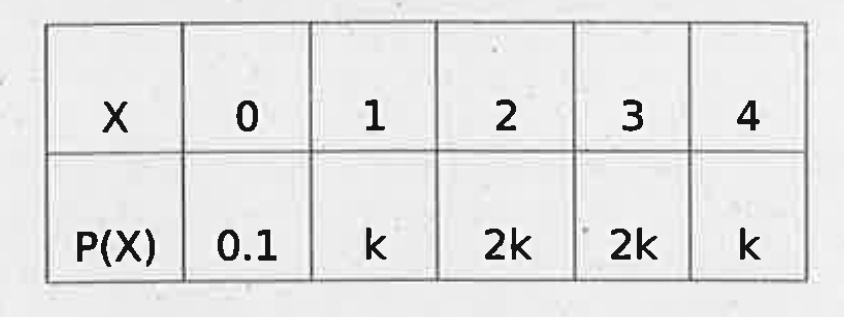
View SolutionThe probability distribution of a random variable X is given in the following table: Find the probability that X lies between 1 and 4.
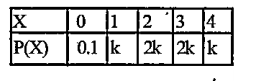
View SolutionThe probability distribution of a random variable X in given in the following table:
Find the mean of X.
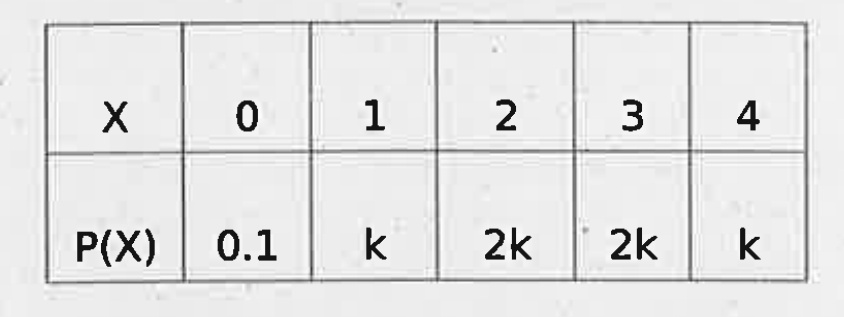
View SolutionThe probability distribution of a random variable X is given in the following table: find variance of X
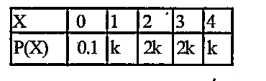
View Solution
EXERCISE questions and complete solutions for chapter QUESTION PAPER 2020 of BODY BOOKS PUBLICATION of Class 12