Complete Solutions to Single Correct Answer Type of chapter PARABOLA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PARABOLA |
| CENGAGE NEW DPP | Single Correct Answer Type |
| Number Of Questions | 46 |
| Academic Year | 2023-24 |
The equation `x^(2) - 2xy +y^(2) +3x +2 = 0` represents (a) a parabola (b) an ellipse (c) a hyperbola (d) a circle
View SolutionThe length of the latus rectum of `3x^(2) -4y +6x - 3 = 0` is (a) 3 (b) 2 (c) `4/3` (d) `3/4`
View SolutionIn the adjacent figure a parabola is drawn to pass through the vertices B,C and D of the square ABCD. If `A(2,1),C(2,3)`, then focus of this parabola is
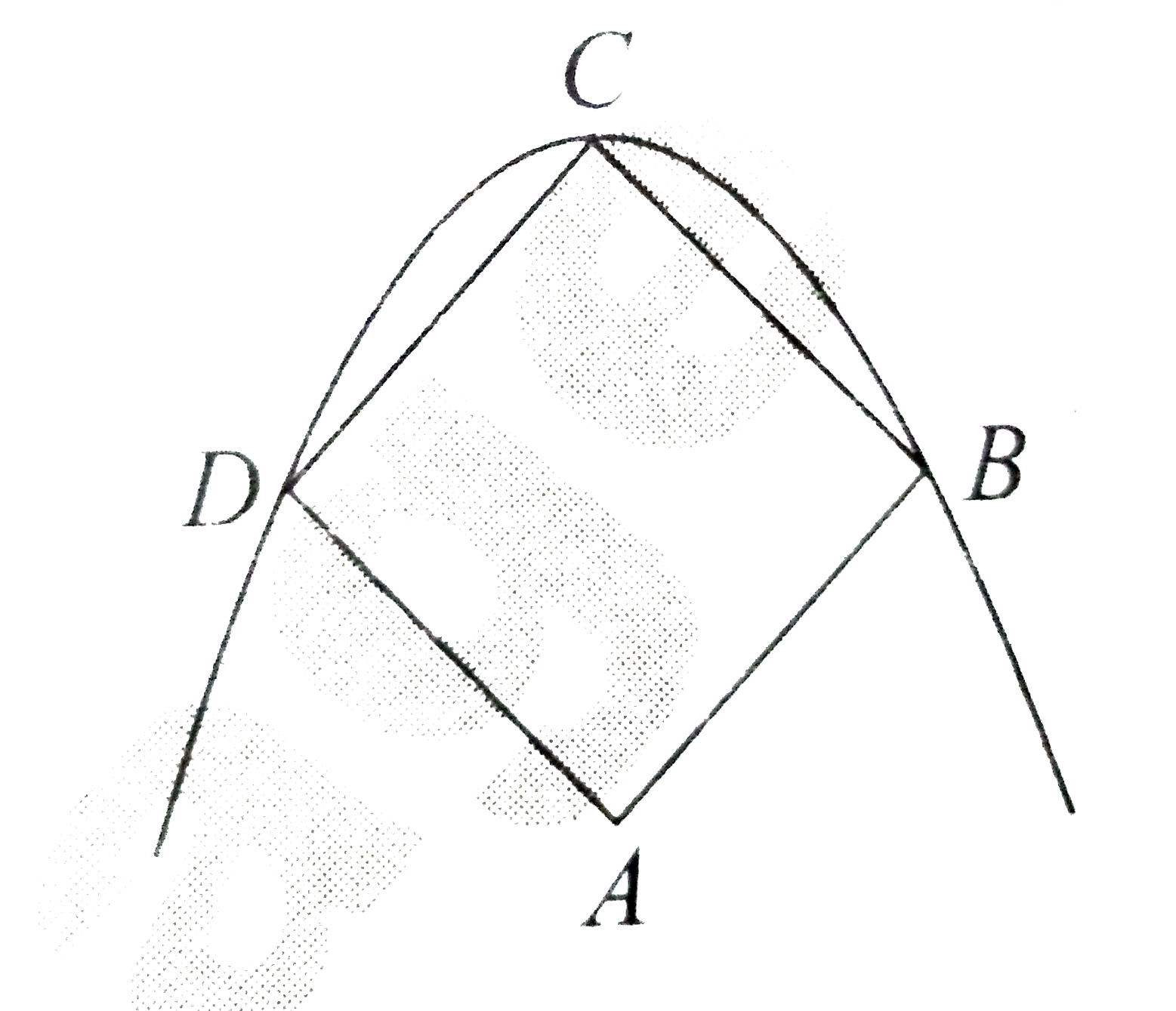
View SolutionLength of the latus rectum of the parabola `sqrt(x) +sqrt(y) = sqrt(a)` is (a) `a sqrt(2)` (b) `(a)/(sqrt(2))` (c) `a` (d) `2a`
View SolutionConsider the parabola `x^(2) +4y = 0`. Let `P(a,b)` be any fixed point inside the parabola and let S be the focus of the parabola. Then the minimum value at `SQ +PQ` as point Q moves on the parabola is (a) `|1 -a|` (b) `|ab|+1` (c) `sqrt(a^(2)+b^(2))` (d) `1-b`
View SolutionIf the points (2,3) and (3,2) on a parabola are equidistant from the focus, then the slope of its tangent at vertex is (a) 1 (b) -1 (c) 0 (d) `oo`
View SolutionLet `A(x_(1),y_(1))` and `B(x_(2),y_(2))` be two points on the parabola `y^(2) = 4ax`. If the circle with chord AB as a dimater touches the parabola, then `|y_(1)-y_(2)|` is equal to
View Solution`y = sqrt(3)x +lambda` is drawn through focus S of the parabola `y^(2)= 8x +16`. If two intersection points of the given line and the parabola are A and B such that perpendicular bisector of AB intersects the x-axis at P then length of PS is
View SolutionIf the point `(2a,a)` lies inside the parabola `x^(2) -2x - 4y +3 = 0`, then a lies in the interval (a) `[1/2,3/2]` (b) `(1/2,3/2)` (c) `(1,3)` (d) `(-3/2,-1/2)`
View SolutionIf AFB is a focal chord of the parabola `y^(2) = 4ax` such that `AF = 4` and `FB = 5` then the latus-rectum of the parabola is equal to (a) 80 (b)`9/80` (c) 9 (d) `80/9`
View SolutionLength of the focal chord of the parabola `(y +3)^(2) = -8(x-1)` which lies at a distance 2 units from the vertex of the parabola is (a) `8` (b) `6sqrt(2)` (c) 9 (d) `5sqrt(3)`
View SolutionLet `A (0,2),B` and C be points on parabola `y^(2)+x +4` such that `/_CBA (pi)/(2)`. Then the range of ordinate of C is (a) `(-oo,0)uu (4,oo)` (b) `(-oo,0] uu[4,oo)` (c) `[0,4]` (d) `(-oo,0)uu [4,oo)`
View Solution`lx +my = 1` is the equation of the chord PQ of `y^(2) = 4x` whose focus is S. If PS and QS meet the parabola again at R and T respectively, then slope of RT is (a) -1/m (b) 1/m (c) 2/m (d) none of the above
View SolutionA line from `(-1,0)` intersects the parabola `x^(2)= 4y` at A and B. Then the locus of centroid of `DeltaOAB` is (where O is origin) (a) `3x^(2) -2x =4y` (b) `3y^(2) -2y = 4x` (c) `3x^(2) +2x=4y` (d) none of these
View SolutionAll the three vertices of an equilateral triangle lie on the parabola `y = x^(2)`, and one of its sides has a slope of 2. Then the sum of the x-coordinates of the three vertices is
View SolutionFind the equations of the chords of the parabola `y^2= 4ax` which pass through the point (- 6a, 0) and which subtends an angle of `45^0` at the vertex.
View SolutionTwo equal circles of largest radii have following property:
(i) They intersect each other orthogonally,
(ii) They touch both the curves `4(y+2) = x^(2)` and `4(2-y) =x^(2)` in the region `x in [-2 sqrt(2),2sqrt(2)]`. Then radius of this circle is
View SolutionLet P and Q are points on the parabola `y^(2)=4ax` with vertex O, such that OP is perpendicular to OQ and have lengths `r_(1) and r_(2)` respectively, then the value of `(r_(1)^(4//3)r_(2)^(4//3))/(r_(1)^(2//3)+r_(2)^(2//3))` is :
View SolutionA line `ax +by +c = 0` through the point `A(-2,0)` intersects the curve `y^(2)=4a` in P and Q such that `(1)/(AP) +(1)/(AQ) =(1)/(4)` (P,Q are in 1st quadrant). The value of `sqrt(a^(2)+b^(2)+c^(2))` is
View SolutionSuppose a parabola `y = x^(2) - ax-1` intersects the coordinate axes at three points A,B and C, respectively. The circumcircle of `DeltaABC` intersects the y-axis again at the point `D(0,t)`. Then the value of t is
View SolutionThe line `x - b +lambda y = 0` cuts the parabola `y^(2) = 4ax (a gt 0)` at `P(t_(1))` and `Q(t_(2))`. If `b in [2a, 4a]` then range of `t_(1)t_(2)` where `lambda in R` is
View SolutionIf the parabola `y=(a-b)x^2+(b-c)x+(c-a)` touches x- axis then the line `ax+by+c=0` (a) always passes through a fixed point (b) represents the family of parallel lines (c) is always perpendicular to x-axis (d) always has negative slope
View SolutionA normal to parabola, whose inclination is `30^(@)`, cuts it again at an angle of (a) `tan^(-1)((sqrt(3))/(2))` (b) `tan^(-1)((2)/(sqrt(3)))` (c) `tan^(-1)(2sqrt(3))` (d) `tan^(-1)((1)/(2sqrt(3)))`
View SolutionIf `(-2,5)` and (3,7) are the points of intersection of the tangent and normal at a point on a parabola with the axis of the parabola, then the focal distance of that point is
View SolutionThe angle of intersection between the curves `x^(2) = 4(y +1)` and `x^(2) =-4 (y+1)` is (a) `pi/6` (b) `pi/4` (c) `0` (d) `pi/2`
View SolutionThe parabolas `y^2=4ax` and `x^2=4by` intersect orthogonally at point `P(x_1,y_1)` where `x_1,y_1 != 0` provided (A) `b=a^2` (B) `b=a^3` (C) `b^3=a^2` (D) none of these
View SolutionSum of slopes of common tangent to `y = (x^(2))/(4) - 3x +10` and `y = 2 - (x^(2))/(4)` is (a) -6 (b) -3 (c) `1/2` (d) none of these
View SolutionThe slope of normal to be parabola `y = (x^(2))/(4) -2` drawn through the point `(10,-1)` is (a) -2 (b) `-sqrt(3)` (c) `-1/2` (d) `-5/3`
View SolutionThe tangent and normal at the point `P(4,4)` to the parabola, `y^(2) = 4x` intersect the x-axis at the points Q and R, respectively. Then the circumcentre of the `DeltaPQR` is (a) `(2,0)` (b) `(2,1)` (c) `(1,0)` (d) `(1,2)`
View SolutionThe point on the parabola `y^(2) = 8x` at which the normal is inclined at `60^(@)` to the x-axis has the co-ordinates as (a) `(6,-4sqrt(3))` (b) `(6,4sqrt(3))` (c) `(-6,-4sqrt(3))` (d) `(-6,4sqrt(3))`
View SolutionIf two distinct chords of a parabola `y^2=4ax` , passing through (a,2a) are bisected by the line x+y=1 ,then length of latus rectum can be a) 2 b) 7 c) 4 d) 5
View SolutionFrom an external point `P ,` a pair of tangents is drawn to the parabola `y^2=4xdot` If `theta_1a n dtheta_2` are the inclinations of these tangents with the x-axis such that `theta_1+theta_2=pi/4` , then find the locus of `Pdot`
View SolutionA variable parabola `y^(2) = 4ax, a` (where `a ne -(1)/(4))` being the parameter, meets the curve `y^(2) +x -y- 2 = 0` at two points. The locus of the point of intersecion of tangents at these points is
View SolutionIf X is the foot of the directrix on the a parabola. PP' is a double ordinate of the curve and PX meets the curve again in Q. Then prove that P' Q passes through the focus of the parabola.
View SolutionLet PQ be the latus rectum of the parabola `y^2 = 4x` with vetex A. Minimum length of the projection of PQ on a tangent drawn in portion of Parabola PAQ is
View SolutionThrough the vertex O of the parabola `y^(2) = 4ax`, a perpendicular is drawn to any tangent meeting it at P and the parabola at Q. Then OP, 2a and OQ are in
View SolutionTangents PQ and PR are drawn to the parabola `y^(2) = 20(x+5)` and `y^(2) = 60 (x+15)`, respectively such that `/_RPQ = (pi)/(2)`. Then the locus of point P is
View SolutionThe locus of centroid of triangle formed by a tangent to the parabola `y^(2) = 36x` with coordinate axes is (a) `y^(2) =- 9x` (b) `y^(2) +3x = 0` (c) `y^(2) = 3x` (d) `y^(2) = 9x`
View Solution`PC` is the normal at P to the parabola `y^2=4ax, C` being on the axis. `CP` is produced outwards to disothat `PQ =CP` ; show that the locus of Q is a parabola.
View SolutionIf three parabols touch all the lines `x = 0, y = 0` and `x +y =2`, then maximum area of the triangle formed by joining their foci is
View SolutionIf `2x +3y = alpha, x -y = beta` and `kx +15y = r` are 3 concurrent normal of parabola `y^(2) = lambda x` then value of k is (a) 3 (b) 4 (c) 5 (d) 7
View SolutionLet `(2,3)` be the focus of a parabola and `x + y = 0` and `x-y= 0` be its two tangents. Then equation of its directrix will be (a) `2x - 3y = 0` (b) `3x +4y = 0` (c) `x +y = 5` (d) `12x -5y +1 = 0`
View SolutionIn the following figure, `AS = 4` and `SP = 9`. The value of SZ is
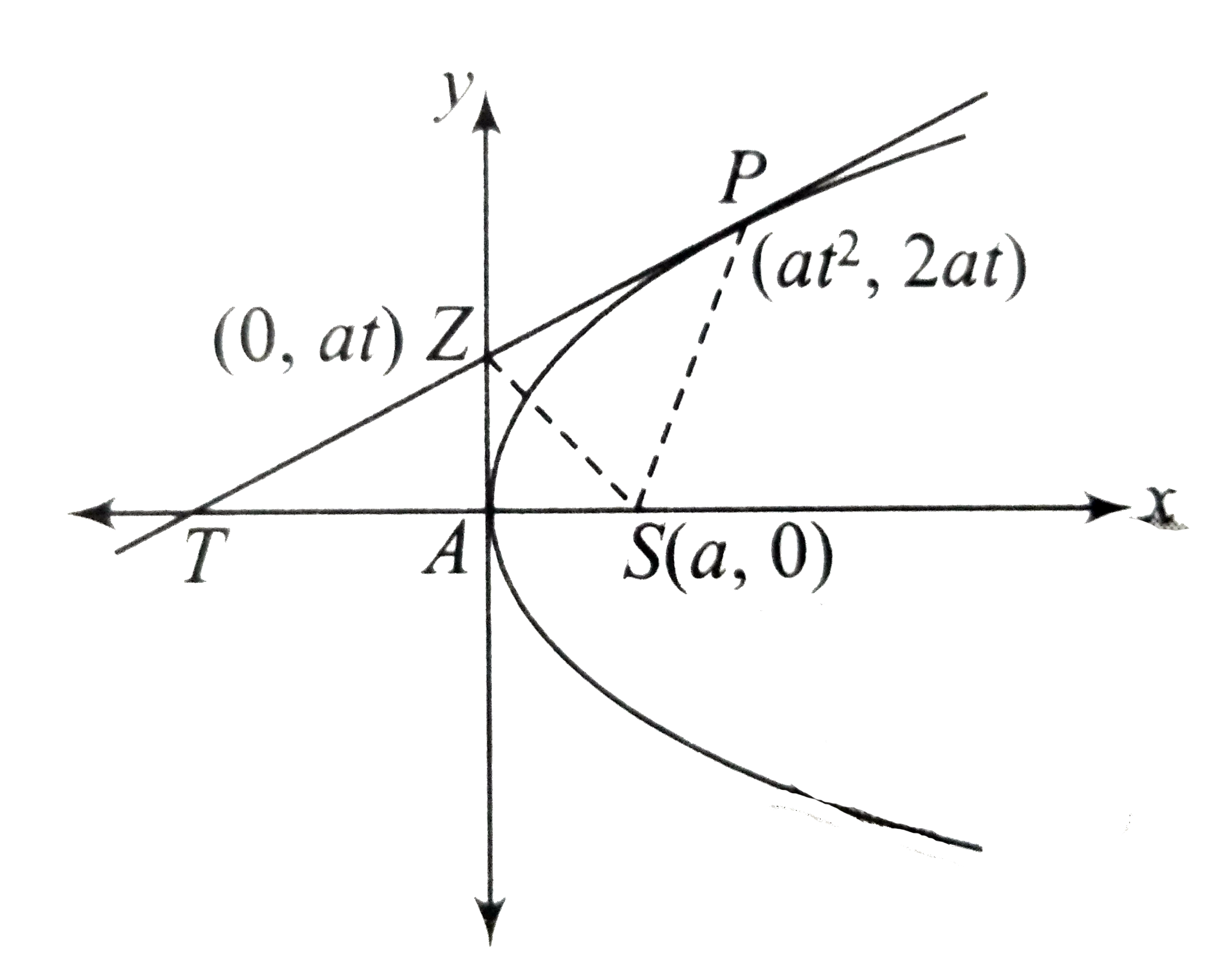
View SolutionTP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in `P` and `Q` , prove that `(TP')/(TP)+(TQ')/(TQ)=1`.
View SolutionThe distance of two points P and Q on the parabola `y^(2) = 4ax` from the focus S are 3 and 12 respectively. The distance of the point of intersection of the tangents at P and Q from the focus S is
View SolutionA parabola having directrix `x +y +2 =0` touches a line `2x +y -5 = 0` at (2,1). Then the semi-latus rectum of the parabola, is
View Solution
Single Correct Answer Type questions and complete solutions for chapter PARABOLA of CENGAGE MATHS (ENGLISH) of Class 12
All Exercises from CENGAGE NEW DPP Class 12 MATHS PARABOLA
- ARCHIVES SINGLE CORRECT ANSWER TYPE
- Comprehension Type
- Concept Applications Exercise 5.1
- Concept Applications Exercise 5.2
- Concept Applications Exercise 5.3
- Concept Applications Exercise 5.4
- Concept Applications Exercise 5.5
- Concept Applications Exercise 5.6
- Concept Applications Exercise 5.7
- EXERCISE (MULTIPLE CORRECT ANSWER TYPE )
- EXERCISE (SINGLE CORRECT ANSWER TYPE )
- ILLUSTRATION 5.1
- ILLUSTRATION 5.10
- ILLUSTRATION 5.11
- ILLUSTRATION 5.12
- ILLUSTRATION 5.13
- ILLUSTRATION 5.14
- ILLUSTRATION 5.15
- ILLUSTRATION 5.16
- ILLUSTRATION 5.17
- ILLUSTRATION 5.18
- ILLUSTRATION 5.19
- ILLUSTRATION 5.2
- ILLUSTRATION 5.20
- ILLUSTRATION 5.21
- ILLUSTRATION 5.22
- ILLUSTRATION 5.23
- ILLUSTRATION 5.24
- ILLUSTRATION 5.25
- ILLUSTRATION 5.26
- ILLUSTRATION 5.27
- ILLUSTRATION 5.28
- ILLUSTRATION 5.29
- ILLUSTRATION 5.3
- ILLUSTRATION 5.30
- ILLUSTRATION 5.31
- ILLUSTRATION 5.32
- ILLUSTRATION 5.33
- ILLUSTRATION 5.34
- ILLUSTRATION 5.35
- ILLUSTRATION 5.36
- ILLUSTRATION 5.37
- ILLUSTRATION 5.38
- ILLUSTRATION 5.39
- ILLUSTRATION 5.4
- ILLUSTRATION 5.40
- ILLUSTRATION 5.41
- ILLUSTRATION 5.42
- ILLUSTRATION 5.43
- ILLUSTRATION 5.44
- ILLUSTRATION 5.45
- ILLUSTRATION 5.46
- ILLUSTRATION 5.47
- ILLUSTRATION 5.48
- ILLUSTRATION 5.49
- ILLUSTRATION 5.5
- ILLUSTRATION 5.50
- ILLUSTRATION 5.51
- ILLUSTRATION 5.52
- ILLUSTRATION 5.53
- ILLUSTRATION 5.54
- ILLUSTRATION 5.55
- ILLUSTRATION 5.56
- ILLUSTRATION 5.57
- ILLUSTRATION 5.58
- ILLUSTRATION 5.59
- ILLUSTRATION 5.6
- ILLUSTRATION 5.60
- ILLUSTRATION 5.61
- ILLUSTRATION 5.62
- ILLUSTRATION 5.63
- ILLUSTRATION 5.64
- ILLUSTRATION 5.65
- ILLUSTRATION 5.66
- ILLUSTRATION 5.67
- ILLUSTRATION 5.68
- ILLUSTRATION 5.69
- ILLUSTRATION 5.7
- ILLUSTRATION 5.70
- ILLUSTRATION 5.71
- ILLUSTRATION 5.72
- ILLUSTRATION 5.73
- ILLUSTRATION 5.74
- ILLUSTRATION 5.75
- ILLUSTRATION 5.76
- ILLUSTRATION 5.77
- ILLUSTRATION 5.78
- ILLUSTRATION 5.79
- ILLUSTRATION 5.8
- ILLUSTRATION 5.80
- ILLUSTRATION 5.81
- ILLUSTRATION 5.82
- ILLUSTRATION 5.83
- ILLUSTRATION 5.84
- ILLUSTRATION 5.85
- ILLUSTRATION 5.9
- JEE ADVENCED SINGLE CORRECT ANSWER TYPE
- LINKED COMPREHENSION TYPE
- Matching Column Type
- MATRIX MATCH TYPE
- MULTIPLE CORRECT ANSWER TYPE
- Multiple Correct Answers Type
- NUMERICAL VALUE TYPE
- Single Correct Answer Type
- SOLVED EXAMPLES 5.1
- SOLVED EXAMPLES 5.10
- SOLVED EXAMPLES 5.11
- SOLVED EXAMPLES 5.12
- SOLVED EXAMPLES 5.13
- SOLVED EXAMPLES 5.14
- SOLVED EXAMPLES 5.2
- SOLVED EXAMPLES 5.3
- SOLVED EXAMPLES 5.4
- SOLVED EXAMPLES 5.5
- SOLVED EXAMPLES 5.6
- SOLVED EXAMPLES 5.7
- SOLVED EXAMPLES 5.8
- SOLVED EXAMPLES 5.9