Complete Solutions to Question Bank of chapter LIMITS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LIMITS |
| CENGAGE | Question Bank |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
If `Lim_(x rarr 0) (1-cosx)/(e^(ax)-bx-1)` exist and is equal to 1, then `(a^(2) + b^(2))` equals
View SolutionIf graph of a function f(x) is shown in the adjacent figure, then `Lim_(x rarr 0^(-)) [(4f(x)-6[f(x)])/(tan(2f(x)-6))]` is equal to
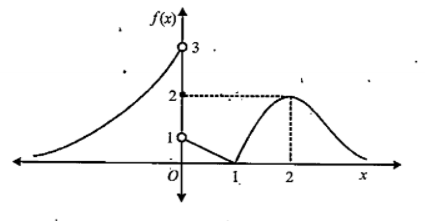 View Solution
View SolutionIf `beta_(1)+beta_(2)+beta_(3)+....+beta_(n) = p` and `Lim_(x rarrp)((3-3tan(pi/4-x))/(sin 2x)) m^(n)`(where m and n are co-prime) then (m+n) equals (where `beta_(1),beta_(2),….beta_(n) are the values of beta)`
View SolutionLet f(x) be a function continuous for all x except at x =0 such that `f^(')(x) gt 0` for `x gt 0` and `f^(')(x) lt 0` for `x lt 0`. If `Lim_(x rarr 0^(+)) f(x) =10, Lim(x rarr 0^(-)) f(x) =15` and f(0) = 12 then the value of `(Lim_(x rarr 0)f(x^(3)-x^(2)))/(Lim_(x rarr0)f(2x^(4)-x^(5)))+(Lim_(x rarr0)[f(x^(3)-x^(2))])/(Lim_(x rarr 0) [f(2x^(4)-x^(5))]), is equal to [Note : [k] denote greatest integer less than or equal to k]
View SolutionLet f(x) =`(sec x)^(cosecx) + (cot x)^(sin x)`. Then the value of `Lim_(x rarr 0^(+)) f(x)` is equal to
View Solution`Lim_(z rarr 0){{max((sin^(-1)x + cos^(-1)x)^(2), min(x^(2)+4x+7))}. (sin^(-1)z)/z]` is equal to (where [.] denotes greatest integer function)
View Solution`((8e^(a))/e)lim_(n rarr oo) ((n/(n+1))^(a) + sin (1/n))^(n))`where `a in Q` (rational number) is equal to
View SolutionIf the value of `lim_(x rarr oo) (root(3)(x^(3)+x^(2)-root(3)(x^(3)-x^(2))` can be expressed as (a/b), where `a, b in N` and a & b are relatively prime numbers), then (a+b) is
View SolutionLet f(x) be a polynomial satisfying `lim_(x rarr oo) (x^(2)f(x))/(2x^(5)+3) = 6` also f(1) = 3, f(3) =7 and f(5) =11, then find the value of ((f(6)+5f(4))/29)
View SolutionLet `L_(1) = Lim_(x rarr 0)(cos(pix)(e^(lambda x)-1)/(pi sin x)` and L_(2) = Lim_(x rarr 0) (In (1-x)+sin 2x)/x` If L_(1) = L_(2)` then the value of `[lambda]` is [Note: `[lambda]` denotes the largest integer less than or equal to lambda].
View SolutionIf `Lim_(c rarr 0) (asinc+btanc)/c^(3) = 3/2`, find the value of |a+2b|.
View Solution`Lim_(n rarr oo) (1-1/2^(2))(1-1/3^(2))(1-1/4^(2))…(1-1/n^(2))` equals
View SolutionThe value of `Lim_(x rarr 0)(sum_(k =1)^(2016){(sinx)/x+2015k})/2016` is [where {x} represents fractional part of x]
View Solution`Lim_(x rarr oo) (30+4sqrtx+7root(3)(x))/(2+sqrt(4x-7)+root(3)(6x-2) )`equals
View SolutionIf `Lim_(x rarr0) ((a sin x + b tan x)/x^(3))= 3/2` then |a+2b| is equal to
View Solution`lim_(x rarr 0)(1/(1+n^(2))+2/(1+n^(2))+3/(1+n^(2))+....+n/(1+n^(2)))` is equal to
View SolutionFind the value of `lim_(n rarr oo)sum_(k=1)^(n)(k^(2)+k-1)/((k+1)!) `.
View SolutionIf `Lim_(x rarr 0)(1-cos(1-cos(1-cosx)))/x^(a) is finite then teh maximum value of a is
View SolutionThe value of `Lim_(x rarr 0)((tanx)^(1/x)+(1+sinx)^(x))` where `x gt0` is equal to
View SolutionLet f(x) be a differentiable function satisfying `f(x+y) = f(x)+f(y) AA x, y in R` and `f^(')(0) =1`.Then `Lim_(x rarr0)(2^(f(tan^(2)x))-2^(f(sin^(2)x)))/(x^(3) f(sin x)) equals
View SolutionLet `lim_(x rarr0) ((8^(x)-2^(x)-4^(x)+1)(128^(x)-16^(x)-8^(x)+1))/x^(4)` is equal to `(lnb)^(4)`, then a/(2b) is
View SolutionFor `n in N, let a_(n) = sum_(k=1)^(n) 2k`and b_(n) = sum_(k=1)^(n)(2k-1)`. Then `Lim_(n rarr oo)(sqrt(a_(n))-sqrt(b_(n)))` is equal to
View SolutionIf `Lim_(x rarr 0) (a sinx + bxe^(x)+3x^(2))/(sin x-2x+tanx) exists and has value equal to L, then the value of (b-L)/a is equal to
View SolutionIf Lim_(x rarr a) (sqrt(x-b)-sqrt(a-b))/(x^(2)-a^(2))(a gt b) = 1/64` and ` Lim_(x rarr oo) (sqrt(x^(2)+ax)-sqrt(x^(2)+bx)) = 2` then the value of a/b, is
View SolutionValue of `lim_(x rarr 0) (sin(2pi secx))/x^(2)` is
View Solution`If `lim_(x rarr 0) (k+cos lx)/x^(2) exists and has the value equal to -4 then find `l^(2)`
View Solution`Lim_(x rarr 0)((3sin x- sin 3x)^(4))/((sec x - cosx)^(6)) is equal to
View Solution`Lim_(x rarr 0)(tanx sqrt (tanx)-sin x sqrt(sinx))/(x^(3).sqrtx)` equals
View Solution`Lim_(x rarr 1)(sin^(2)(x^(3)+x^(2)+x-3))/(1-cos(x^(2)-4x+3))` has the value equal to
View SolutionLet `f(x) = (In (x^(2)+e^(x)))/(In(x^(4)+e^(2x)))`, then value o f`Lim_(x rarr oo)(1/(f(x)))^(f(x))` is equal to
View Solution
Question Bank questions and complete solutions for chapter LIMITS of CENGAGE MATHS (HINGLISH) of Class 12
All Exercises from CENGAGE Class 12 MATHS LIMITS
- Comprehension Type
- ComprehensionType
- Examples
- Exercise (Comprehension)
- Exercise (Matrix)
- Exercise (Multiple)
- Exercise (Numerical)
- Exercise (Single)
- Exercise 2.1
- Exercise 2.2
- Exercise 2.3
- Exercise 2.4
- Exercise 2.5
- Exercise 2.6
- Exercise 2.7
- Exercise 2.8
- JEE Advanced Previous Year
- JEE Main Previous Year
- Multiple Correct Answer Type
- Multiple Correct Answers Type
- Question Bank
- Single Correct Answer Type
