Complete Solutions to Exercise (Single) of chapter TRIGONOMETRIC FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | TRIGONOMETRIC FUNCTIONS |
| CENGAGE NEW | Exercise (Single) |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
If `5tantheta =4," then " (5sintheta-3costheta)/(5sintheta+2costheta)` is equal to
01:42View SolutionIf `tantheta =-4/3," then " sintheta` is
01:39View SolutionIf `sinx+cosecx=2," then "sin^nx+cosec^nx` is equal to
01:35View SolutionIf `tantheta+sintheta=mandtantheta-sintheta=n`,then
04:10View SolutionIf `cosectheta-cottheta=q`, then the value of `cosectheta` is
01:26View SolutionIf `(sinx)/a=(cosx)/b=(tanx)/c=k ,` then `b c+1/(c k)+(a k)/(1+b k)` is equal to `k(a+1/a)` (b) `1//k(a+1/a)` `1/(k^2)` (d) `a/k`
03:33View SolutionIf `sec^4theta+sec^2theta=10+tan^4theta+tan^2theta", then "sin^2theta=`
02:35View SolutionIf `x=(2sintheta)/(1+costheta+sintheta),t h e n(1-costheta+sintheta)/(1+sintheta)` is equal to `1+x` (b) `1-x` (c) `x` (d) `1/x`
03:59View SolutionIf `secalpha` and `cosecalpha` are the roots of the equation `x^2-px+q=0`, then (i)`p^2=q(q-2)` (ii)`p^2=q(q+2)` (iii)`p^2+q^2=2q` (iv) none of these
02:13View SolutionWhich of the following is not the quadratic equation whose roots are `cosec^2thetaand sec^2theta`?
05:31View SolutionIf `sinx+sin^2x=1`, then find the value of `cos^(12)x +3cos^(10)x + 3 cos^8x + cos^6x-1 `
02:24View Solution`3(sintheta-costheta)^(4)+6(sintheta+costheta)^(2)+4(sin^(6)theta+cos^(6)theta)=?`
03:17View SolutionIf `sinx+sin^2x=1` then the value of `tan^8x-tan^4x-2tan^2x+1` will be equal to 0 (b) 1 (c) 2 (d) 3
02:30View Solution`(1+tanalphatanbeta)^2+(tanalpha-tanbeta)^2=`
01:49View SolutionLet `A_0A_1A_2A_3A_4A_5` be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths the line segments `A_0A_1, A_0A_2` and `A_0A_4` is
05:42View SolutionA circle is drawn in a sectore of a larger circle of radius r, as shown in fugure. The smaller circle is tangent to the two bounding radii and the are of the sector. The radius of the smaller circle is
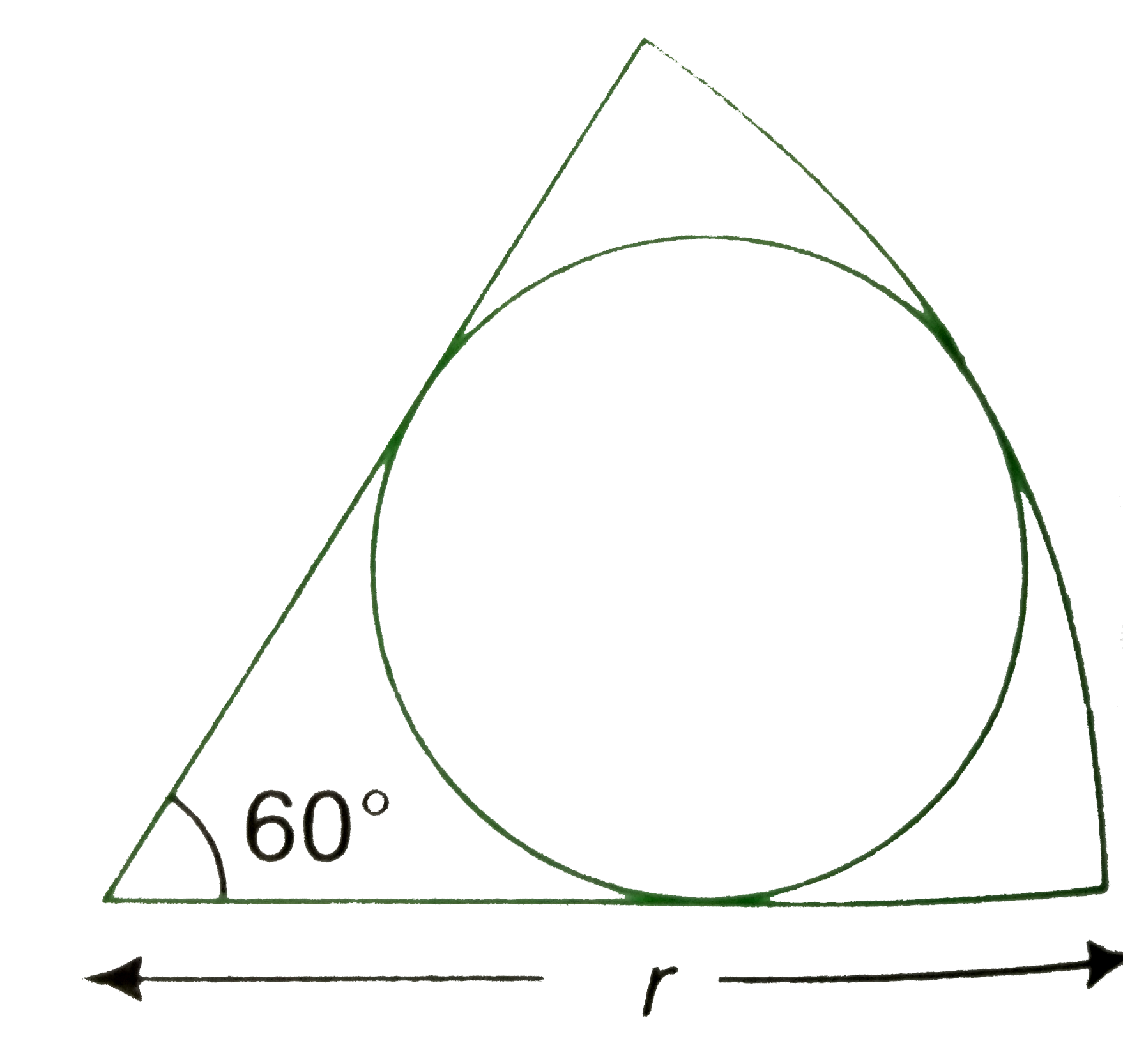 02:40View Solution
02:40View SolutionA right triangle has perimeter of length 7 and hypotenuse of length `3.` If `theta` is the larger non-right angle in the triangle, then the value of `costhetae q u a ldot` `(sqrt(6)-sqrt(2))/4` (b) `(4+sqrt(2))/6` `(4-sqrt(2))/3` (d) `(4-sqrt(2))/6`
08:55View SolutionGiven that the side length of a rhombus is the geometric mean of the length of its diagonals. The degree measure of the acute angle of the rhombus is `15^0` (b) `30^0` (c) `45^0` (d) `60^0`
02:38View SolutionWhich of the following is correct?
01:54View SolutionThe equation `sin^2theta=(x^2+y^2)/(2x y),x , y!=0` is possible if
02:12View Solutionif `sin^2theta=(x^2+y^2+1)/(2x)` then `x` must be
02:16View Solution`sec^2 x=(4xy)/(x+y)^2` is true if and only if
06:05View SolutionIf `sintheta_1+sintheta_2+sintheta_3=3," then "costheta_1+costheta_2+costheta_3` is equal to
02:07View SolutionIf `sinx+siny+sinz+sinw=-4" then the value of "sin^400x+sin^300y+sin^200z+sin^100w` is
02:55View SolutionThe minimum value of the expression `sin alpha + sin beta+ sin gamma`, where `alpha,beta,gamma` are real numbers satisfying `alpha+beta+gamma=pi` is
02:42View SolutionIf `1+sinx+sin^2x+sin^3x+oo` is equal to `4+2sqrt(3),0
02:05View SolutionThe value of expression `(2sin^2 91^0-1)(2sin^2 92^0-1)(2sin^2 180^0-1)` is equal to 0 (b) `1` (c) `2^(90)` (d) `2^(90)-90`
04:25View SolutionIf `sinA=sin^2B and 2cos^2A=3cos^2B` then the triangle ABC is
04:09View SolutionIf `sintheta+costheta=1/5and 0lethetaltpi" then "tantheta` is
02:49View SolutionIf `piltalphalt(3pi)/2lt" then "sqrt((1-cosalpha)/(1+cosalpha))+sqrt((1+cosalpha)/(1-cosalpha))` is equal to
02:27View SolutionIf `0 < alpha < pi/ 6` then `alpha(cosec alpha)` is
01:59View SolutionThe least value of `2sin^2theta+3cos^2theta` is
02:37View SolutionThe greatest value of `sin^4theta+cos^4theta` is
02:40View SolutionIf `f(x)=sin^6x+cos^6x ,` then range of `f(x)` is `[1/4,1]` (b) `[1/4,3/4]` (c) `[3/4,1]` (d) none of these
02:18View SolutionThe minimum value of `atan^2x+bcot^2x` equals the maximum value of `asin^2theta+bcos^2theta` where `a > b > 0.` The `a/b` is 2 (b) 4 (c) 6 (d) 8
02:28View SolutionRange of `f(theta)=cos^2theta(cos^2theta+1)+2 sin^2theta` is
04:38View SolutionIf `0
01:44View SolutionIf `theta_igt0" for "1lethetalenandtheta_1+theta_2+theta_3+...+theta_n=pi`then the greatest value of sum `sintheta_1+sintheta_2+sintheta_3+…+sintheta_n` is equal to
02:03View SolutionThe set of values of `lambda in R` such that `sin^2theta+costheta=lambdacos^2theta` holds for some `theta,` is `(-oo,1]` (b) (`-oo,-1]` `varphi` (d) `[-1,oo` )
04:17View SolutionLet `A=sin^8theta+cos^14theta, " then "A_("max")` is
01:42View SolutionMinimum value of `y=256 sin^2x+324cosec^2x AA x inR` is
02:20View SolutionIf a and b are positive quantities, `(a gt b)` find minimum positive value of `(a sectheta- b tantheta)`
03:30View SolutionIf `y=(sinx+cosecx)^2+(cosx+secx)^2` then the minimum value of `y,AAx in R`, is
02:39View SolutionThe variable `x` satisfying the equation `|sinxcosx|+sqrt(2+tan^2+cot^2x)=sqrt(3)` belongs to the interval `[0,pi/3]` (b) `(pi/3,pi/3)` (c) `[(3pi)/4,pi]` (d) none-existent
02:55View SolutionIf the equation `cof^4x-2cos e c^2x+a^2=0` has at least one solution, then the sum of all possible integral values of a is equal to a. 4 b. 3 c. 2 d. 0
04:45View SolutionIf `cos^2x-(c-1)cosx+2cgeq6` for every `x in R ,` then the true set of values of `c` is `(2,oo)` (b) `(4,oo)` (c) `(-oo,-2)` (d) `(-oo,-4)`
04:44View SolutionIf the inequality `sin^2x+acosx+a^2>1+cosx` holds for any `x in R ,` then the largest negative integral value of a is `-4` (b) 3 (c) `-2` (d) `-1`
03:23View SolutionIf `(3pi)/4ltalphaltpi," then "sqrt(2cotalpha+1/sin^2alpha)`is equal to
02:17View SolutionThe value of `sectheta/sqrt(1-cos^2x)+cosx/(sqrt(1+cot^2theta))" for "theta in (pi,(3pi)/2)` is
01:21View SolutionThe minimum value of the function `f(x)=sinx/(sqrt(1-cos^2x))+cosx/sqrt(1-sin^2x)+tanx/sqrt(1-sec^2x-1)+cotx/sqrt(1-cosec^2x-1)` whenever it is defined is
04:14View SolutionIf `abs(cos theta{sin theta+sqrt(sin^2theta+sin^2alpha)})lek`, then the value of k
06:39View SolutionIn which of the following intervals the inequality, `sinx < cos x < tanx < cot x` can hold good ?
03:36View SolutionTh range of k for which the inequaliity `kcos^2x-kcosx+1>=0 AA x in(-oo,oo) is`
04:00View SolutionThe value of `cospi/7+cos(2pi)/7+cos(3pi)/7+cos(4pi)/7+cos(5pi)/7+cos(6pi)/7+cos(7pi)/7` is 1 (b) `-1` (c) 0 (d) none of these
02:21View SolutionThe numerical value of `tanpi/3+2tan(2pi)/3+4tan(4pi)/3+8tan(8pi)/3` is equal to `-5sqrt(3)(b)-5/(sqrt(3))` (c) `5sqrt(3)` (d) `5/(sqrt(3))`
02:15View SolutionThe expression `3[sin^4(3/2pi-alpha)+sin^4(3pi+alpha)]-2[sin^6(1/2pi+alpha)+sin^6(5pi-alpha)]` is equal to
06:57View SolutionThe value of the expression `log_10(tan6^@)+log_10(tan12^@)+log_10(tan18^@)+...+log_10(tan84^@)` is
04:54View Solution
Exercise (Single) questions and complete solutions for chapter TRIGONOMETRIC FUNCTIONS of CENGAGE MATHS (HINGLISH) of Class 12
