Complete Solutions to Question Bank of chapter PROBABILITY AND STATISTICS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY AND STATISTICS |
| CENGAGE | Question Bank |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
If two events `A` and `B` are such that `P(A^(l))=0.3`, `P(B)=0.4` and `P(A nn B^(l))=0.5`, then `P(B/(A uu B^(l)))` equals
View SolutionMr. `A` has six children and atleast one child is a giel, then probability that `Mr, A` has 3 boys and 3 girls, is
View SolutionThere are 4 horizontal and `.6` vertical equispaced lines as shown. If a rectangle is randomly selected then probability that is a square is
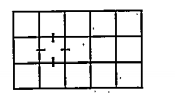 View Solution
View SolutionA bag contains `(2 n+1)` boins. It is known that `n` of these coin have a head on both sides, whereas the remaining `(n+1 ) coins are fair A coin is selected at random from the bag and tossed once. If the probability the toss results in a head is `(31)/(42)`, then `n` is equal to
View SolutionThree distinct integers are randomly selected from the set of integers from 16 to 30 (inclusive). Probability that their sum is even, is
View SolutionA number `x` is chosen at random from the set `(1,2,3,4, …., 100`. Define the event `A` - the chosen number `x` satisfies, `((x-10)(x-50))/(x-30) ge 0 .` Then `P(A)` is equal to
View Solution`A` and `B` stand in a ring along with 10 other pèrsons. If the arrangement is at random, the probability that there are exactly 3 persons between `A` and `B`, is
View SolutionA `2 xx 2` matrix is formed with entries from the set `0,1`. The probebility that it is singular, is
View SolutionTwo boys `A` and `B` find the jumble of `n` ropes lying on the floor. Each takes hold of one loose end randomly. If the probability that they are both holding the same rope is `1/(101)` then the number of ropes is equal to
View SolutionOn a normal standard dic one of the 21 dots from any one of the six faccs is removéd at random with each dot equally likely to be chosen. The die is then rolled. The probability that the top face has an odd number of dots is
View SolutionMiss `C` has either Tea or Coffee at moming break. If she has tea one morning, the probability she bas tea the next moming is `0.4`. If she has coffee one morning, the probability she has coffee next moming is `0.3`. Suppose she has coffee on a Monday morning. The probability that she has tea on the following Wednesday morning is
View SolutionA bowl hes 6 red marbles and 3 green marbles. The probebility that a blind folded person will draw u red marble on the second draw from the bowl without replacing the marble from the first draw, is
View SolutionLot `A` consists of `3 G` and `2 D` articles. Lot `B` consists of `4 G` and `1 D` article. A new lot `C` is formed by taking 3 articles from `A` and 2 from `B`. The probability that an article chosen at random from `C` is defective, is
View SolutionAperson throws fourdice simultaneously. The probability of getting different numbers on all four dice, is
View SolutionLet `A` and `B` are cvents of an experiment of `P(A)=1/4`, `P(A uu B)=1/2` then value of `P(B l A^C)` is `1 / k` then value of `k` is
View SolutionLet `S=1,2,3,4,5,6,7,8,9,10`. Two subscts `A` and `B` of `S` are chosen randomly with replacement with `B` chosen after `A`. The probability that `A` is a subset of `B` can be expressed as `(p^a)/(q^8)` for some s `p` and `q`. Find the value of `((b)/(a)+p+q)`.
View SolutionThe probability that a positive two digit number selected at random has its tens digit at least three more than its unit digit is
View SolutionOf all the system of equations in `x, y` and `x`
`a x+b y+z=c`
`x+y=d`
`y+e z=1`
formed by choosing `a, b, c, d, e` from the set `0,1,2,3`, `4,5,6,7,8` with replacement, the probability it does not possess a unique solution is `(2^m)/(3^n) ` (in lowest terms), `m, n in N`. The value of `(n-m)` isView SolutionIf the papers of 4 students randomly đistributed for checking among 7 teachers, then the probability that all the 4 papers are checked by exactly 2 teachers is `n i m` where `n, m` are 'natural numbers and `H C F(n, m)=1`. Then number of positive divisors of `(n+m)` is
View Solution`A` six faced fair dice is thrown until 2 comes, then the probability that 2 comes in even number of trials is (dice having six faces numbered `1,2,3,4,5` and 6 )
View SolutionIf a variable takes the discrete values `p+4, p-7/2, p-5/2, p-3, p-2, p+1/2, p-1/2, p+5 (p>0)`, and the median `p-K` then find `k`
View SolutionThe variance of 20 observations is 5 . If eech observation is multiplied by 2 then the new variance of the resulting observations, is:
View SolutionThe mean weight of 9 items is 15 . If one more item is added to the series, the mean becomes 16 . The value of `10^( th) ` item is
View SolutionConsider the frequency distribution of the given pumber If mean of the distribution is cqual to 3 , then the value of `f` is
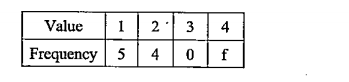 View Solution
View SolutionIf `m` and `sigma^2` are the mean and variance of random variable `x`, whose distribution is given by then sum of `m` and `sigma^2` is
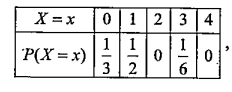 View Solution
View Solution`x_1, x_2 …. x_(34)` are numbers such that `x_i=x_i+1-150 forall i in1,2,3, ... 9` and `x_i+1-x_i+2=0` `forall f in10,11,12, ... 33`, then median of `x_j x_2, ... x_34` is
View SolutionThe mean of 5 observations is 4 and their variancé is `52 .` If three of them are `1,2,6` then the sum of other two
View SolutionIf `x_1, x_2, .. x_18` are observations sach the ` underset(j =1)overset(18)sum(x_j-8)= 9` and `underset(j =1)overset(18)sum(x_j-8)^2 = 45`, then the standard deviation. of these observations is:
View SolutionTwo cards are drawn without replacement from a wellshuffled deck of 52 cards. Let `X` be the number of face cards drawn, then the sum of mean and variance of `X` will be.
View SolutionLet `x_1, x_2 ... x_n` be `n` observations sach that `sum x_i^2=200` and `sum x_i=40` then least integral value of `n`
View SolutionIf in a frequency distribution, the mean and median are 25 and 26 , then its mode is approximately.
View SolutionThe mean of two samples of sizes 200 and 300 were found to be 25,10 respectively. Their standard deviation were 3 and 4 respectively. The variance of combined sample of size 500 is
View SolutionThe variance of first 20-natural numbers is
View SolutionIf the coefticient of skewness of distribution is `0.32 .` If its standard deviation is `6.5` and mean is `29.6`, then the mode of the distribution is given by
View SolutionFind the mean deviation from the mean for the following data: `6,7,10,12,13,4,8,20`
View SolutionFor the following observations of marks of 5 students of a tutorial group:
Marks out of `25: 8,12,13,15,22`
Then the standard deviation of the above observation isView SolutionCalculate the mean deviation from the median of the following data:
 View Solution
View Solution
Question Bank questions and complete solutions for chapter PROBABILITY AND STATISTICS of CENGAGE MATHS (HINGLISH) of Class 12
