Complete Solutions to Question Bank of chapter PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCE of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCE |
| CENGAGE | Question Bank |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
The area of a right triangle is 6864 square units. If the ratio of its legs is `143: 24`, then find the radius of the circle inscribed in the triangle.
View SolutionIn `Delta A B C`, the incircle touches the sides `B C, C A` and `A B` respectively at `D, E` and `F .` If the radius of the incircle is 4 units and `B D, C E` and `A F` are consecutive integers, then find the perimeter of the A B C`.
View SolutionThe altitudes from the angular points `A, B` and `C` on the opposite sides `B C, C A` and `A B` of `Delta A B C` 'are 210,195 and 182 respectively. If the length of the side `B C` can be expressed as rational `m/n` (in the lowest form), then find `(m+n) .`
View SolutionSum of all the radii of the circles touching the coordinate axes and the line `3 x+4 y=12`, is
View SolutionIn triangle `A B C` if `sin A sin B sin C` is equal to `10^(-3)` and `(A B)(B C)(C A)` is equal to `10^3` then the area of triangle `A B C`, is
View SolutionIn `Delta A B C`, if angle C=3 angle A, B C=27` and A B=48 , then find the length of the side A C .
View SolutionThe sides `a, b` and `c` of triangle `A B C` satisfy `(a+1) b c=` 12, `(b+1) c a=4` and `(c+1) a b=4`If area of triangle equals `(sqrt4 n^2-1)/4 n` where `n in N`, then find the value of `n .`
View SolutionThe area of a triangle `A B C` is equal to `(a^2+b^2-c^2)`, where `a, b` and `c` are the sides of the triangle. The value of `tan C` equals
View SolutionTriangle `A B C` has `A C=13, A B=15` and `B C=14 .` Let `O`be the circumcentre of the A B C`. If the length of perpendicular from the point ' `O` ' on `B C` can be expressed as a rational `m/n` in the lowest form then find `(m+n)`.
View SolutionConsider a point `P(4, sqrt2)` points `Q, R` which respectively lie on the lines `y=x` `y=0 .` If `Delta P Q R` is formed and its minimum perimeter is `a`, then `a` is equal to
View SolutionWith usual notation, in triangle `A B C, a=4, b=5, c=7`. Let internal angle bisector through `A` intersect side `B C` at `D`, then the value of `(A I)/(I D)` is
View SolutionIf circumradius and inradius of A B C` be 10 and 3 respectively, then find the value of `a cot A+b cot B+c` `cot C`
View SolutionFigure shows triangle `A B C` such that `A B=A C=5, B C= 6. Point `D` is on `B C` such that `(B D)/(D C)=1/2`, then square of length of side `A D` is
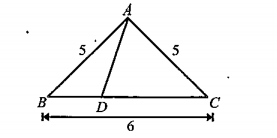 View Solution
View SolutionIn acute `Delta A B C`, ratio of distance of orthocentre from vertex `A` and distance of circumcentre from side `B C` is equal to
View SolutionIf a, b, c are in A.P. then the numerical value of `3 tan A/2 tan C/2` is
View SolutionIn A B C, if `A B=10, B C=8, C A=12` and a point `D` is taken on `A B` such that A D: D B is 3:2 , then the square of length of `C D` is
View SolutionConsider the triangle pictured as shown. If `0 lt alpha lt pi / 2` then the number of integral values of `c` is
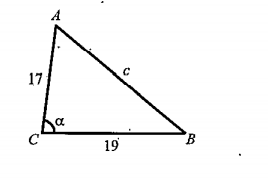 View Solution
View SolutionIn A B C, if `a=2, r=1/(sqrt3)` and `angle A=60^circ` and the length of median from vértex `B` is `k`, value of `k^2` is [Note: All the symbols used have usual meaning in A B C .]`
View SolutionGiven a O A B` has sides `O A=7, A B=11` and `O B=14`. `T` is 'the mid point of `O A` and a point `S` is taken on `B T` dividing it in the ratio `2: 1` then square of area of S O T` is
View SolutionThe angle of elevation of the top of a tower by standing on a horizontal'plane at a point `A` is `15^(circ)`. After walking `40 m` from `A` towards tower this angle becomes `30^(circ) .` The height of the tower (in metres) is
View SolutionAn aeroplane flying at a height 300 metre above the ground passes vertically above another plane at an instant when the angles of elcvation of the two planes from the same point on the ground are `60^(circ)` and `45^(circ)` respectively. Then the height of the lower plane from the ground (in metres) is
View SolutionThe angles of elevation of the top of a tower at the top and the foot of a pole of height `10 m` are `30^(circ)` and `60^(circ)` respectively. The height of the towcr (in metres) is
View SolutionA flagstaff on the top of the tower 80 meter high, subtends an angle `tan ^(-1)(1/9right)` at a.point on the ground 100 -meters away from the foot of the tower. Find the height of the flag-staff (in metres)
View SolutionA 6 -ft tall man finds that the angle of elevation of the top of a 24 -ft-high pillar and the angle of depression of its hase are complementary angles. The distance of the man (in metres) from the pillar is
View SolutionA flagstaff `5 ~m` high is placed on a building `25 m` high. If the flag and building both subtend equal angles on the observer at a height `30 m`, the distance between the observer and the top of the flag (in metres) is
View SolutionA man standing on a level plane oberves the elevation of the top of a pole to be `theta`. He then walks a distance equal to double the height of the pole and then finds that the elevation is now `2 theta`. Then `cot theta` is equal to
View SolutionTwo parallel towers `A` and `B` of different heights are at some distance on same level ground. If angle of elevation of a point `P` at `20 m` height on tower `B` from a point `Q` at `10 m` height on tower `A` is `theta` and is equal to half the-angle of elevation of point `R` at `50 m` height on `A` from point `P` on `B`, then sine of `theta` is
View SolutionA man from the top of a 100 metres high tower sees a car moving towards the tower at an angle of depression of `30^(circ)`. After some time, the angle of depression becomes `60^(circ) .` The distance (in metres) travelled by the car during this time is
View SolutionFrom the top of a light house, `60 m` high with its base at sea level, the angle of depression'of a boat is `15^(circ) `.The distance of the boat (in metres) from the light house is
View SolutionAt a point `A`, the angle of elevation of a tower is such that its tangerit is `5/(12)`, on walking `120 m` nearer the tower the tangent of the angle of elevation is `3/4`. The height of the tower (in metres) is
View SolutionA man of height 6 ft. observe the top of a tower and the foot of the tower at angle of `.45^(circ)` and `30^(circ)` of elevation and depression respectively. The height of the tower (in metres) is
View SolutionFor a man, the angle of elevation of the highest point of the temple situated east of him is `60^(circ) .` On walking 240 metres to north, the angle of elevation' is reduced to `30^(circ)`, then the height of the temple is
View Solution
Question Bank questions and complete solutions for chapter PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCE of CENGAGE MATHS (HINGLISH) of Class 12
