Complete Solutions to Exercises Subjective of chapter MAGNETIC FIELD AND MAGNETIC FORCES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC FIELD AND MAGNETIC FORCES |
| CENGAGE PHYSICS | Exercises Subjective |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
An `alpha-`particle is describing a circle of radius 0.45 m in a field of magnetic induction of 1.2 T. Find its speed, frequency of rotation and kinetic energy. What potential difference will be required to accelerate the particle so as to give this much of the energy to it? The mass of `alpha-`particle is `6.8 xx 10^(-27) kg` and its charge is twice the charge of proton, i.e.,`3.2 xx 10^(-19) C`.
View SolutionIn a trapeze-shaped structure, two rigid wires of negligble mass support a conducting bar of mass m and length L as shown in Fig. A source of emf is applied to the wires so that a current I flows through the bar. A uniform magnetic field `vec B` is perpendicular to the plane of the wires and bar.
a. Compute the current that the source of emf must provide so that there is no tension in the wires.
b. If the current is reduced to half the value computed in (a) and the plane of the structure is moved through an angle `theta`, compute the tension in the wires and the magnitude of the net unbalanced force on the bar at the instant it is released from this angle.

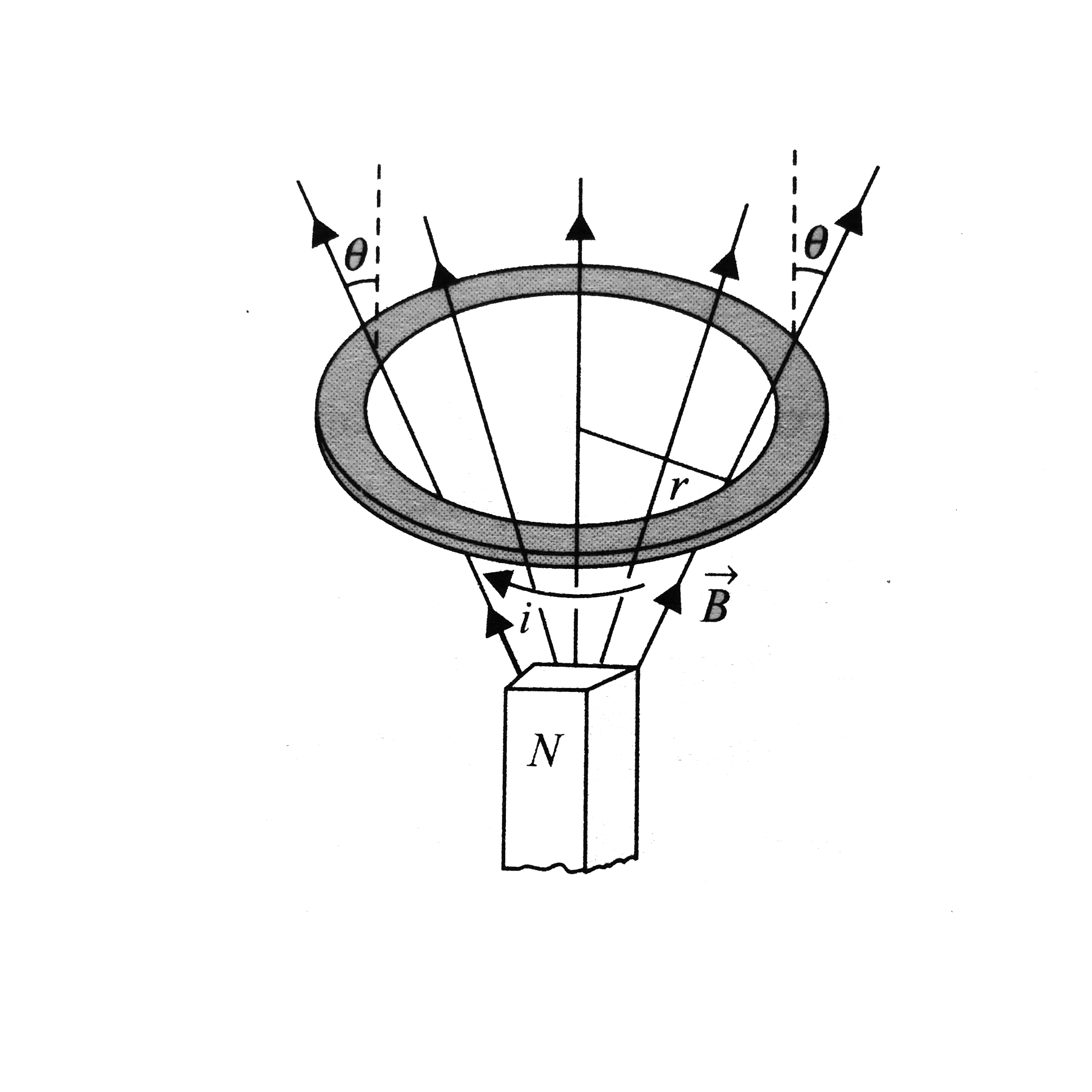
View SolutionA strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle `theta` with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?
View SolutionA wheel with 4 spokes is placed with its plane perpendicular to a uniform magnetic field B of magnitude 0.5 T. The field is directed into the plane of the paper and is present over the entire region of the wheel as shown in Fig. When the switch S is closed, there is initial current of 6 A between the axis and the rim and the wheel begins to rotate. Resistances of the spokes are 1, 2, 4 and 8 `Omega`, respectively. Resistance of rim is negligible.
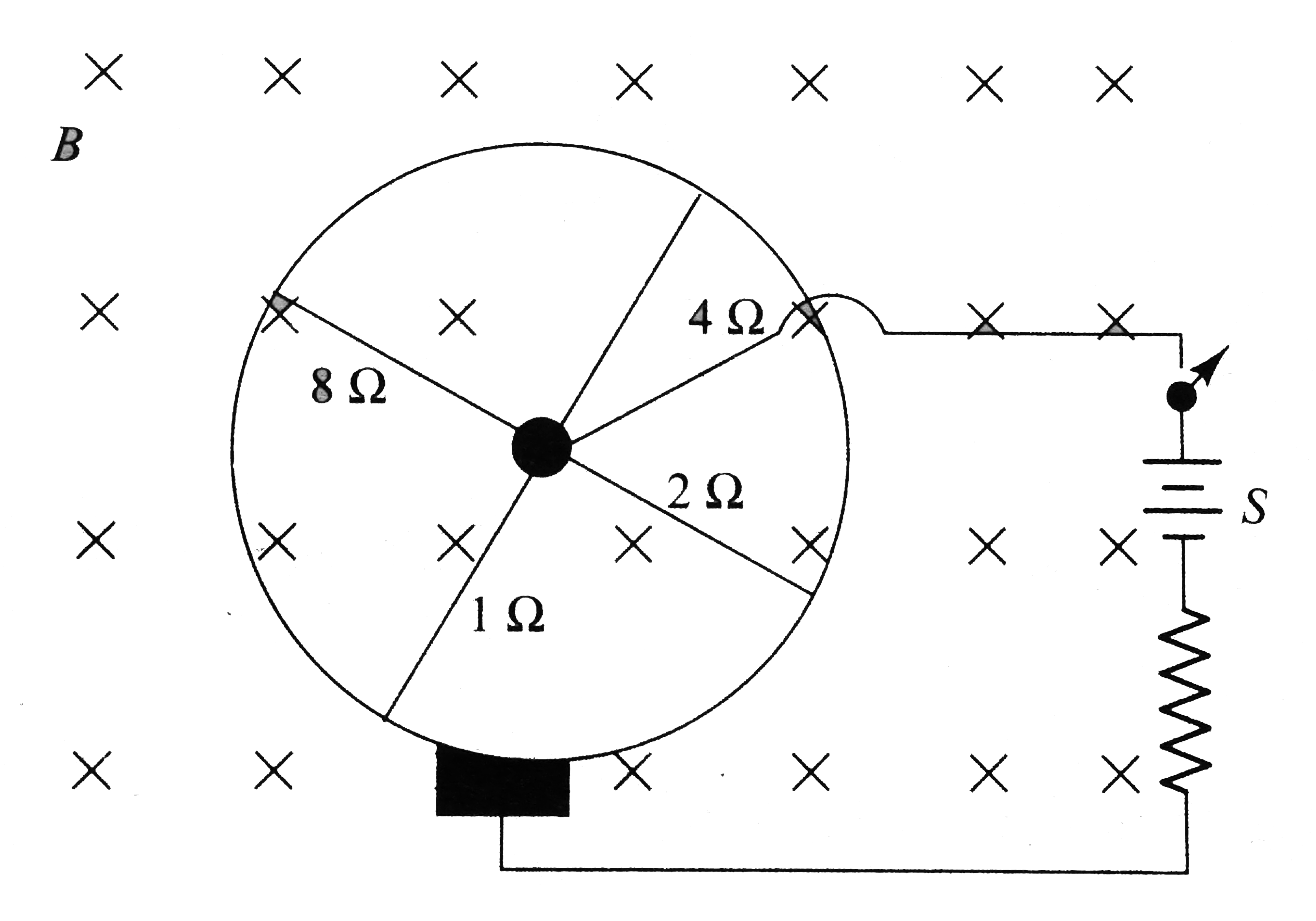
a. What is the direction of rotation of the wheel?
b. Radius of the wheel is 0.2 m. Calculate initial torque acting on the wheel.
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines `x=0 and x=a.` Beyond the line `x=a` (i.e., in the region `xgta`), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line `x=a`.
b. the pitch of the helix formed after the particle enters the region `xgea.` (Mass of the particle is m.)
View SolutionA charged particle +q of mass m is placed at a distanced from another charged particle -2q of mass 2m in a uniform magnetic field B as shown in Fig. 1.28. If the particles are projected towards each other with same speed v,

a. find the maximum value of projected speed `v_m` so that the two particles do not collide.
b. find the time after which collision occurs between the particles if projection speed equals `2v_m.`
c. Assuming the collision to be perfectly inelastic, find the radius of the particle in subsequent motion. (Neglect the electric force between the charges.)
View SolutionA conducting wire of length `l` is placed on a rough horizontal surface, where a uniform horizontal magnetic field B perpendicular to the length of the wire exists. Least values of the forces required to move the rod when a current `I` is established in the rod are observed to be `F_1` and `F_2 (lt F_1)` for the two possible directions of the current through the rod, respectively. Find the weight of the rod and the coefficient of friction between the rod and the surface.
View SolutionA small circular coil with a mass of m consists of N turns of fine wire and carries a current of I. The coil is located in a uniform magnetic field of B with the coil axis orginally parallel to the field direction.

a. What is the period of small angle oscilations of the coil axis around its equilibrium position, assuming no friction and no mechanical force?
b. If the coil is rotated through an angle of `theta` from its equilibrium position and then released, what will be its angular speed when it passes through equilibrium position?
View SolutionTwo metal strips, each of length, each of length l, are clamped parallel to each other on a horizontal floor with a separation b between them. A wire of mass m line on them perpendicularly as shown in figure. A vertically upward magnetic field of strenght B exists in the space. The matal strips are smooth but the cofficient of freiction between the wire and the floor is `mu`. A current i is established when the switch S is closed at the instant `t=0`. Discuss the motion of the wire after the switch is closed. How far away from the strips will the wire reach?

View SolutionA metal rod of mass 10 gm and length 25 cm is suspended on two springs as shown in Fig. 1.131. The springs are extended by 4 cm. When a 20 A current passes through the rod, it rises by 1 cm. Determine the magnetic field assuming acceleration due to gravity to be `10 ms^-1.`

View Solution
Exercises Subjective questions and complete solutions for chapter MAGNETIC FIELD AND MAGNETIC FORCES of CENGAGE PHYSICS (HINGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS MAGNETIC FIELD AND MAGNETIC FORCES
- Archives Assertion-reasion
- Archives Comprehension
- Archives Fill In The Blank
- Archives Integer
- Archives Multiple Correct
- Archives Single Correct
- Archives True /false
- Comphension Based
- Comprehension type
- Exercise 1.1
- Exercise 1.2
- Exercise1.3
- Exercises Assertion -reasoning
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises Subjective
- Illustration
- Multiple
- Multiple Correct Answer type
- Single Correct Answer Type
- Solved Example
- Subjective
- Subjective type