Complete Solutions to Question Bank of chapter THERMAL PROPERTIES OF MATTER of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | THERMAL PROPERTIES OF MATTER |
| CENGAGE PHYSICS | Question Bank |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
Thegraph `A B` shown in the figure is a plot of temperature of a body in degree Celsius and degree Fahrenheit. If the slope of line'AB is `(x)/(y)`, find `(x+y)`.
'(##CEN_KSR_PHY_JEE_C13_E01_001_Q01##)'
View SolutionTwo spherical black bodies, `A` and `B`, having radii `r_(A)` and `r_(D)`, where `r_(B)=2 r_(A)` emit radiations with peak intensities i at wavelengths `400 nm` and `800 nm`, respectively. If their temperature are `T_(A)` and `T_(B)` respectively, in Kelvin scale, their emissive powers are `E_(A)` and `E_(B)` and energies emitted per second are `P_(A)` and `P_(g)`, then find `((P_(A))/(P_(B)))`.
View SolutionA ring consisting of two parts `A D B` and `A C B`. of same conductivity `K` carries an amount of heat `H`. The `A D B` part is now replaced with another metal keeping the temperature `T_(1)` and `T_(2)` constant. The heat carried increases to `2 H .` The conductivity of the new `A D B` part is `(x)/(3) K .` Find the value of `x`, (Given: `(A C B)/(A D B)=3` ) .
'(##CEN_KSR_PHY_JEE_C13_E01_003_Q02##)'
View SolutionTwo identical solid spheres have the same temperature. One of the spheres is cut into two identical pieces, The intact spheres radiates energy `Q` during a given small time interval. During the same interval, the two hemispheres radiate a total energy `Q^(r)`. The ratio `Q^(prime) / Q` is equal to
View SolutionA cup of tea cools from `80^(circ) C` to `60^(circ) C` in one min. The ambient temperature is `30^(circ) C`. In cooling from `60^(circ) C` to ` 0^(circ) C` how much time (in s) will it take?
View SolutionIce starts forming in lake with water at `0^(circ) C` when the atmospheric temperature is `-10^(circ) C`. If the time taken for `1 cm` of ice be `7 h`, then the time taken (in hours) for the thickness of ice to change from `1 cm` to `2 cm` is
View SolutionThere is a small hole in a container. At what temperature (in `K` ) should it be maintained in order that it emits one. calorie of energy per second per `metre^(2)` ?
View SolutionEmissivity `e` is a property of surface. Suppose for `t` surface emissivity e varies with Kelvin temperature `T` as `e=C T` (C is constant ). If energy emission rate at temperature `600, K` from the surface is `160 W`, what will be the energy emission rate (in watt) at `300 K` ?
View SolutionThe energy radiated by a black body at `2000 K` is found to have the maximum value at a wavelength `1.5 mu m`. Its emissive power being `8000 W m^-2`. When the body is cooled at a temperature `T`, the emissive power decreases to `500 W m^(-2)`. At this temperature `T`, the maximum of energy distribution occurs at a wavelength `mu (m)`.
View SolutionIn a `10 m` deep lake, the bottom is at a constant temperature of `4^(circ) C`. The air temperature is constant at `-4^(circ) C`. The thermal conductivity of ice is 3 times that of water. Neglecting the expansion of water on freezing, the maximum thickness (in m ) of ice will he
View SolutionA system receives heat continuously at the rate of 10 W. The temperature of the system becomes constant at `70^(circ) C` when the temperature of the surrounding is `30^(circ) C`. After the heat is switched off, the system cools from `50^(circ) C` to `49.9^(circ) C` in `1 min`. Find the heat capacity `(in (kJ) / (circ) C` of the system.
View SolutionA and B are two points on a uniform metal ring whose centre is C. The angle `A C B=theta, A` and `B` are maintained at two different constant temperatures. When `theta=180^(circ)` i the rate of total heat flow from `A` to `B` is `1.2 W`. When `theta=90^(circ)`, this rate (in watt) will be
View SolutionA piece of ice (heat capacity `=2100^(circ) (J) (kg)^(-1)(circ) C^(-1)` and latent heat `=3.36 xx 10^5 Jkg^(-1)` ) of mass `m` grams is at `-5^(circ) C` at atmospheric pressure. It is given `420 J` of heat so that the ice starts melting. Finally when the ice-water mixture is in equilibrium, it is found that `1 g` of ice has melted. Assuming there is no other heat exchange in the process, the value of `m` is
View SolutionTwo identical rectangular rods of metal are welded end to end in series between temperature `0^(o) C` and `100^(circ) C` and `10 J` of heat is conducted (in steady state process) through the rod in `2.00 min`. If 5 such rods are taken and joined as shown in the figure maintaining the same temperature difference between `A` and `B`, then the time in min in which `20 J` of heat will flow through the rods is
'(##CEN_KSR_PHY_JEE_C13_E01_014_Q03##)'
View Solution`5 g` of steam at `100^(circ) C` is mixed with `10 g` of ice at `0^(circ) C`. At equilibrium, the mixture contains `p` gram of steam. Find `(p+q)`. (Given: `s_(water ))=1` cal `g^(-1)/^ C^(-1), L_(f)=80 (cal) / (g), L_(v)=540`(cal) / (g)` )
View SolutionThe variation of lengths of two metal rods `A` and `B` with change in temperature are as shown in the figure. The ratio of `(alpha_(B))/(alpha_(A))` is (Here `alpha_(A)=` Linear coefficient of thermal expansion of rod `A_(3) alpha_(B)=` Linear coefficient of thermal expansion of `rod B` .
'(##CEN_KSR_PHY_JEE_C13_E01_016_Q04##)'
View SolutionTwo taps, `A` and `B` supply water at temperatures `10^(circ)` and `50^(circ) C`, respectively. Tap `A` alone fills the tank in `1 h` and tap `B` alone fills the tank in `3 h`. If both the taps are opened simultaneously in an empty tank, then the final temperature of the water in the completely filled tank is found to be `5 a` (`overset(o) \ C` ). Find the value of `a`. Neglect loss of heat to the surrounding and heat capacity of the tank,
View SolutionWater of volume 2 liter in a container is heated with a coil of `1 kW` at `27^(circ) C`. The lid of the container is open and energy dissipates at rate of `160 J / s`. In how much time (in `s` ) temperature will rise from `27^(circ) C` to `77^(circ) C ?` (Given: Specific heat of water is `4.2 kJ / kg)`
View SolutionA baby's bath should be at a temperature of `30^(circ) C`. There is `10 kg` water at `12^(circ) C` in the bath tub. How much water (in kg ) with temperature `50^(circ) C` should be added to achieve the desired temperature?
View Solution`2 g` steam at `100^(circ) C` is mixed with `5 g` ice at `-40^(circ) C` in an ideal calorimeter. The final temperature (in `overset(o) \ C` ) of system is (Givea: `L_(r)=500 cal g, S_(ice)=0.5 cal g^(-1)overset(o) \ C^(-1)` `S_(w) = 1 cal g^(-1)/overset(o) \ C^(-1), L_(f)=80 (cal) / (g))`
View SolutionIt is to cool down `(3)/(4) kg` of water from `80^(circ) C` to `40^(circ) C` by putting `0^(circ) C` ice into it. What minimum volume (in litre) should the vessel have to prevent the water from overflow?
View SolutionA refrigerator converts `100 g` of water at `25^(circ) C` into ice at `-10^(circ) C` in `1 h` and `50 min`. The quantity of heat (in calorie) removed per min is (specific heat of ice `=0.5` cal `(g)^(-1 circ) C^(-1)`, specific heat of water `=1 (cal) (g)^(-1)/ ^circC^(-1)`, latent. heat of fusion `-80 (cal) / (g)` )
View SolutionA calorimeter of negligible heat capacity contains `50 m`. of water at `40^(circ) C`. The water cools to `35^(circ) C` in `50 min`. The water is now replaced by another liquid of equal volume at `40^(circ) C`. The time taken (in min) for the temperature to become `35^(circ) C` under similar condition is [density of liquid `=0.8` ' (density of water), specific heat of liquid `0.5` (specific heat of water)]
View SolutionA calorimeter contains `50 g` of water at `50^(circ) C`. The temperature falls to `45^(circ) C` in `10 min`. When the calorimeter contain `100 g` of water at `cdot 50^(circ) C`, it takes 15 min' for the temperature to become `45^(circ) C`. Find the water equivalent (in g) of the calorimeter. (Assume Newton's law of cooling)
View SolutionA heating curve has been plotted for a solid object as. shown in the figure. If the mass of the object is `200 g`. 'then Iatent heat of vaporization for the material of the object is `(n)/(2) xx 10^(6) J / kg `.If power supplied to the object is constant and equal to `1 kW`, then find the value of `n`.
'(##CEN_KSR_PHY_JEE_C13_E01_025_Q05##)'
View SolutionIn an experiment of measuring specific heat of a liquid, a stream of liquid flows at a steady rate of `5 g / s` over an electrical beater dissipating `135 W` and a temperature rise of `5 K` is observed. On increasing the rate of flow to `10 g / s`, the same temperature rise is produced with `(a)` dissipation of `235 W`. Find the specific heat `J g^(-1) K^(-1))` of the liquid. (Assume heat loss to the surrounding in both the cases is same.)
View SolutionThe specific heat of a metal at low temperatures varies according to `S=(4 / 5) T^(3)`, where `T` is the absolute temperature, Find the heat energy (in SI unit) needed to rate the temperature of unit mass of the metal from `T=1 K` to `T=2 K`
View SolutionTwo identical square rods of metal are welded end to end as shown in figure (i), 20 calories of heat flows through it in 4 minutes. If the rods are welded as shown in figure (ii), the same amount of heat will flow through the rods in
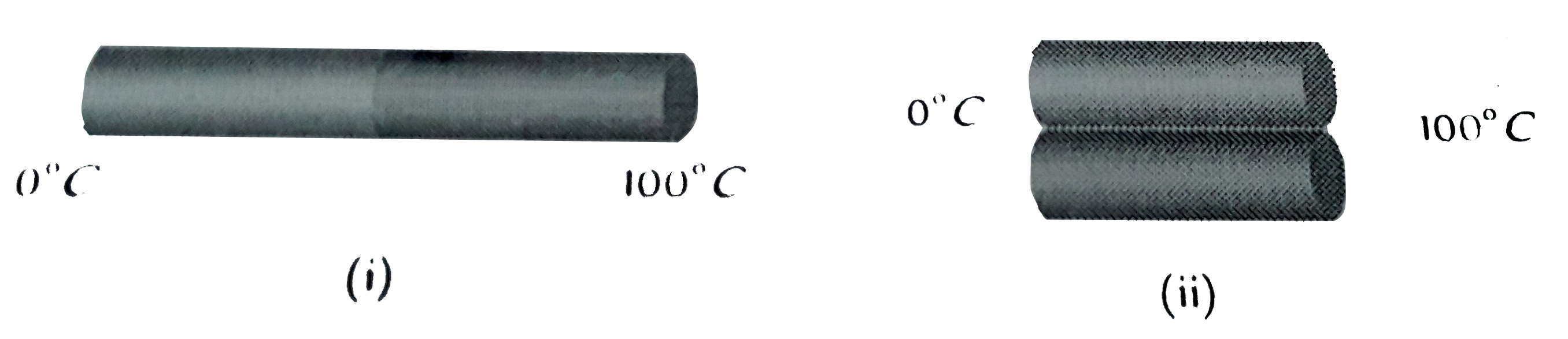
View SolutionHeat is supplied to a certain amount of ice at a constant rate for 9 min. For' the first 1 min, the temperature rises uniformly with time, Then the temperature remains constant for the next 5 min and after that again temperature rises at uniform rate for last `3 min`. If the ratio of magnitude of final temperature to initial temperature is `P^(circ) C`, then find the 'value of `4 P`. (Given: `S_ (ice )=0.5 (cal) (g)^(-1)/overset(o) \ C^(-1), L_(f)=80 (cal g).
View SolutionTwo rods shown in the figure have identical geometrical dimensions. They are in contact with two heat bath at temperature `100^(circ) C` and `0^(circ) C`. The temperature of the junction is `70^(circ) C`. If the rods are interchanged, then temperature of the junction is found to be `10 a^(circ) C`. Find the value of `a`.
'(##CEN_KSR_PHY_JEE_C13_E01_030_Q07##)'
View SolutionTwo different rods A and B are kept as shown in the figure. The variation of temperature of different cross-sections is plotted Find the ratio" of thermal conductivities of `B` to `A`.
'(##CEN_KSR_PHY_JEE_C13_E01_031_Q08##)'
View SolutionA clock pendulum made of invar has a period of `2 s` at `20^(circ) C`. If the clock is used in a climate where average temperature is `40^(circ) C`, what correction (in seconds) may be necessary at the end of 10 days to the time given by clock? `(alpha_(invar ))=7 xx 10^(-7)/overset(o) \ C^(-1), 1day =8.64 xx 10^(4) s )`. Give answer in nearest integer
View SolutionA steel tube, whose coefficient of linear expansion is `18 xx 10^(-6)` per `overset(o) \ C` contains mercury, whose coefficient of volumetric expansion is `180 xx 10^(-6)` per `overset(o) \ C`. The volume of mercury contained in the tube is `10^(-5) m^(3)` at `0^(circ) C`, and it is desired that the length of the mercury column should remain constant at all normal temperatures. This is achieved by inserting into the mercury column a rod of silica, whose thermal expansion is negligible. The volume of silica is given as `eta xx 10^(-5) m^3`. Find the value of `eta`.
'(##CEN_KSR_PHY_JEE_C13_E01_033_Q09##)'
View SolutionAn experiment is carried out under pressure `P_(0)=100 cm` of Hg and consists of a U tube of uniform cross-section 'in 'vertical position as shown in the figure. Now end A of the tube is closed and gas in the tube is heated so that gas expands and mercury spills out. During the process, it is seen that the pressure of enclosed gas is directly proportional to the volume of gas. Find `l_(0)` (in m ).
'(##CEN_KSR_PHY_JEE_C13_E01_034_Q10##)'
View SolutionA rod has variable coefficient of linear expansion `alpha=(x)/(5000)`. If the length of the rod is `1 m`, then determine the increase in length of the rod (in cm ) on increasing the temperature of the rod by `100^(circ) C`.
'(##CEN_KSR_PHY_JEE_C13_E01_035_Q11##)'
View SolutionA `30.0 cm` long metal rod expands by `0.0650 cm` when its temperature is raised from `0^(circ) C` to `100^(circ) C`. A second rod of different metal and of the same length expands by `0.0350 cm` for the same rise in temperature, A third composite rod, also `30.0 cm` long, is made up of pieces of each of the above metals placed end to end and expands by `0.0580 cm` when temperature is increased from `0^(circ) C` to `100^(circ) C`. Find the length (in `cm` ) of the smaller portion of the composite rod at `0^(circ) C`.
View SolutionTwo conductors `A` and `B` each of cross-section area `5 cm^2` are connected in series. Variation of temperature (in `overset(o) \ C` ) along the length (in cm ) is as shown in the figure. If thermal conductivity of A is `200 J m^(-1) s^(-1)/overset(o) \ C^(-1)` 'and thermal conductivity of `B` is `k` (in `J m^(-1) s^(-1)/overset(o) \ C^(-1)` ), then find `sqrt((k)/(8 sqrt(3)))`.
'(##CEN_KSR_PHY_JEE_C13_E01_037_Q12##)'
View SolutionA rod of negligible heat capacity has length `40 cm`, area of cross-section `1.0 cm^2` and thermal conductivity `100 W m^(-1)overset(circ) \ C^(-1)`. The temperature of one end is maintained at `0overset(o) \ C` and that of the other end is slowly and linearly varied 'from `0^(circ) C` to `60^(circ) C` in `10 min`. Assuming no loss of heat through the sides', find the total heat transmitted (in J) through the rod in these `10 min`.
View SolutionThree rods `A B, B C` and `B D` of same length `l` and cross-sectional area `A` are arranged, The end `D` is immersed in ice whose mass is `440 g`. Heat is being supplied at constant rate of `200 (cal) / (s)` from the end A. The time (in s) in which whole ice will melt is (Given:`k` (thermal condactivity) `=100` cal `m^(-1) s^(-1)/overset(o) \ C^(-1), A=` 10 cm^2, l=1 m`, latent heat of fusion of ice is 80 cal g.)
'(##CEN_KSR_PHY_JEE_C13_E01_039_Q13##)'
View SolutionAs shown in the figure, two large black plane surfaces are maintained at constant temperature `T_(1)` and `T_(2) (T_(1) gt T_(2))`. Two thin black plates are placed between the two surfaces and in parallel to them. After some time, steady conditions are obtained. The ratio of heat transfer rate between plate-1 and plate-3 to the ratio of original (when plate-3 and plate- 4 was not present) heat transfer rate between plate-1 and plate-2 in steady state is `eta`. Find `(1)/(eta)`.
'(##CEN_KSR_PHY_JEE_C13_E01_040_Q14##)'
View Solution
Question Bank questions and complete solutions for chapter THERMAL PROPERTIES OF MATTER of CENGAGE PHYSICS (HINGLISH) of Class 12