Complete Solutions to QUESTION BANK of chapter THERMODYNAMICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | THERMODYNAMICS |
| CENGAGE PHYSICS | QUESTION BANK |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
The figure shows two paths through which a gas can be taken from state `A` to state `B`. If the ratio of work done by the gas in the two paths is `x / y`, then find `(x+y)`.
'(##CEN_KSR_PHY_JEE_C15_E01_001_Q01##)'
View SolutionThe efficiency of Carnot engine is "0.6" . It rejects "20J" of heat to the sink. The work done by the engine is
View SolutionSuppose `0.5` mol of an ideal gas undergoes an isothermal expansion as energy is added to it as heat `Q`. The given graph shows the final voiume `V_(f)` versus `Q`. The temperature(in K ) of the gas is (use `ln 9=2` and `R=(25)/(3)` `J (mol)^(-1) K^(-1)` ).
'(##CEN_KSR_PHY_JEE_C15_E01_003_Q02##)'
View SolutionA thermodynamic process undergoes a cyclic process as shown. Find the quantity of heat supplied (in joule) to the system in one complęte cycle.
'(##CEN_KSR_PHY_JEE_C15_E01_004_Q03##)'
View SolutionA heat engine with a thermal efficiency of 40% does 100 J of work per cycle. How much heat (in J) is exhausted to the cold reservoir per cycle?
View SolutionA gas is found to obey `P^(2) V=` constant. The inital temperature and volume of gss are `T_(0)` and `V_(0)`. If the gas expands to volume `3 V_(0)`, then the final temperature of gas is `sqrt(n) T_(0)`. Find `n`.
View SolutionA diatomic gas `(gamma=1.4)` does 2000J of work when it is expanded isobarically. Find the heat given to the gas in the above process (in kJ).
View Solution5.61 of helium gas at STP is adiabatically compressed to `0.7 L` Taking the initial temperature to be `T_(1)`, the work done in the process is `(x)/(y) R T_(1)`. Find `(x+y)`, `(R=` Universal gas constant `)`
View SolutionA certain quantity of an ideal gas takes up `56 J` of heat in the process `A B` and `360 J` in the process `A C`, as shown in the graph below. The adiabatic constant for the gas is.
'(##CEN_KSR_PHY_JEE_C15_E01_009_Q04##)'
View SolutionAn ideal gas is expanding such that `P T^(2)=` constant. The coefficient of volume expansion of the gas is `(A)/(T)`, where `T` is temperature in Kelvin and `P` is pressure, Find the value of A.
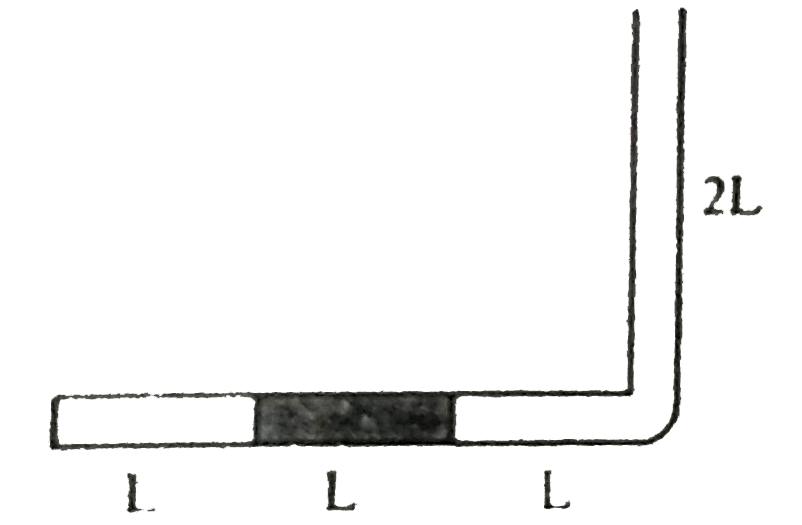
View SolutionThe narrow tube with one of its ends sealed as shown in the figure, is in a vertical plane. In the 3L long horizontal part of the tube a mercury column of length L blocks some oxygen gas of length L. The outside air - pressure of `p_(0)` equals with the pressure of a mercury column of height L. Increasing the temperature of the surrounding, the volume of the blocked gas doubles while the gas absorbs `Q=7J` of heat from its surroundings. How much work (in Joule) is done by the expanding gas?
View SolutionThe figare shows two paths that may be taken by a gas from an initial point `i` to final point `f`. Padh 1 consists of an isoubermal expansion (work is `50 J` in mugnitude), an isothermel compression (work is `30 J` in magnitude), an adiabatic expansion (work is `40 J` in magnitude) and dhen an adiabatic compression (work is `25 J` in magnitude). Find the magnitude of change in intemal energy (in J) in path 2 , i.e., in path AFGE.
'(##CEN_KSR_PHY_JEE_C15_E01_012_Q06##)'
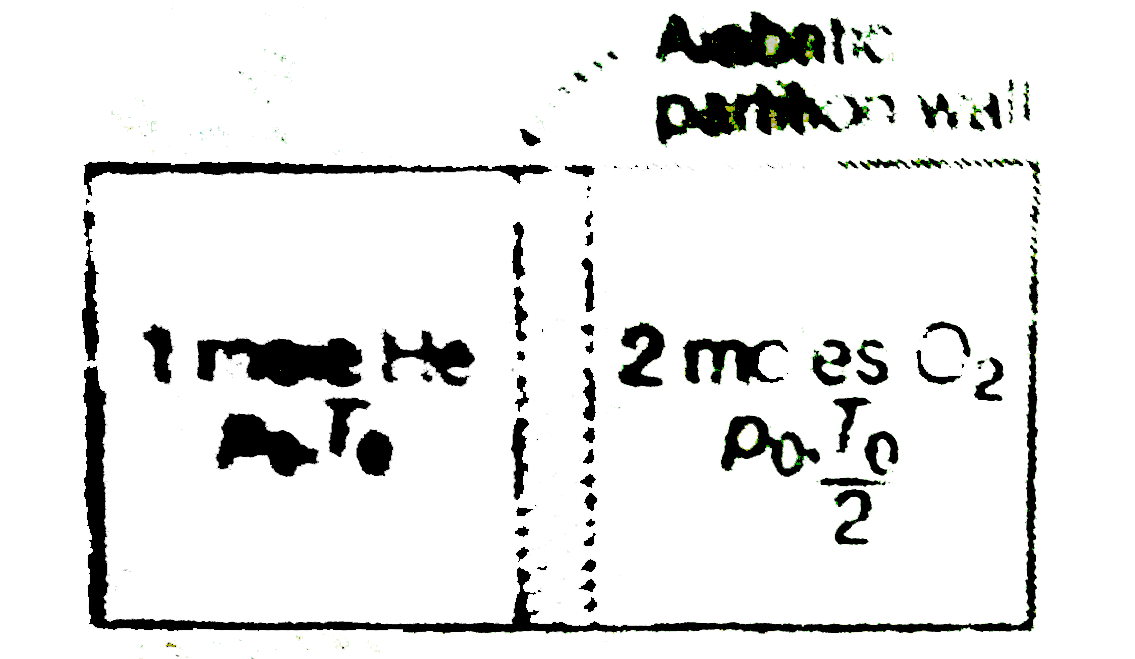
View SolutionConsider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are `T_(0)` and `p_(0)` and the right chamber are `(T_(0))/(2)` and `p_(0)` respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes `p=(4n)/(13)p_(0)`. Find the value of n.
View SolutionA glass tube of length 76 cmi is in inverted position. `A` column of air is trapped with some mercury as shown in the figure. The tube contains 1 mol of atr at `300 K`. Atmospheric pressure remsins constant at `76 cm` of mercury. Temperature of air column is slowly decressed by `30 K`. If the net heat lost (in joule) by the air column is found to be `alpha`, then find the value of `(alpha)/(175)` - (Take `gamma_(air )=` `1.4` and `R=(25)/(3) J mol^(-1) K^(-1)` ) (Neglect surface tension)
'(##CEN_KSR_PHY_JEE_C15_E01_014_Q08##)'
View SolutionThe amount of work done by a gas which is being isobarically heated from `27^(circ) (C)` to `127^(circ) (C)` in a vessel closed by a movable piston with a cross-sectional area of `20 cm^(2)` and weighing `5 kg` in the following two cases is: (1) `w_(1)`, when the vessel is arranged horizontally (Figure a), and (2). w_(2)`, when the vessel is arranged vertically (Figure b). If the initial volume of the gas is 6 litres, then find `(w_(1)+w_(2))` in joule. Assume standard atmaspheric pressure `=100 kPa` and neglect friction.
'(##CEN_KSR_PHY_JEE_C15_E01_015_Q09##)'
View SolutionOne mole of an ideal monoatomic gas is taken from state A to state B through the process `P=3/2 T^(1//2)` It is found that its temperature increases by 100 K in this process. Now it is taken from state B to C through a process for which internal energy is related to volume as `U= 1/2 V^(1//2)` Find the total work performed by the gas (in Joule) if it is given that volume at B is `100 m^(3)` and at C it is `1600m^(3)` [Use `R= 8.3 J //mol-K`]
View SolutionOne mole of monatomic gas is taken through cyclic process shown below. Temperature at `A, T_(A)=300 K`. The process `A B` is defined as `P T=` constant. If the work done in the process `A B` is `(-k R)`, then find `k .(R=` Universal gas constant)
'(##CEN_KSR_PHY_JEE_C15_E01_017_Q10##)'
View SolutionAn ideal monatounic gas of mass `M` is taken through a cyclic process `A B C`. The process `A B` is `P_(p)=` constant. Totál work done by the gas in the process is `-(alpha)/(beta) M (P_(0))/(P_(0)) .` Find `(alpha+beta) .`
'(##CEN_KSR_PHY_JEE_C15_E01_018_Q11##)'
View SolutionIn a cyclic thermodynamio process, an ideal gas is first compressed at constant 'volume whilc its internal energy is increased by `350 J`. Then it expands adiabatically until it rctarns to its original pressure. Finally, the gas is returned isobarically to its original state when `60.0 J` of work is performed on the gas while its internal energy decteases by `200 J`. If the change in intema! cnergy (in SI unit) during the adiabatic expansión is `X`, then find the value of `(X+500)`, Assumic the gas is ideal with `C_(p)=` 20.8 J mol ^(-1) K^(-1)` and `C_(v)=12.5 J mol^(-1) K^(-1)`
View SolutionSome gas `(C_(p) / C_(v)=y=1.25)` follows the cyclo `A B C D A` as shown in the figure. Find the ratio of the energy given by the gas to its surroundings during thie isochorie section of the cycle to the work done in expension of the gas đuring the isobaric section of the cycle.
'(##CEN_KSR_PHY_JEE_C15_E01_020_Q12##)'
View SolutionOne mole of helium in a vessel gets heat from outside and starts expanding to make its volume 2 times the original volume. The heat capacity of the gas in this process is constant and is `(R)/(2)`. What is the final temperature (in `(K)` ) of the gas, if the initial temperature is `200 K` and initial pressure is `40 (kPa)` ? (Here, `R` -Universal gas constant)
View SolutionOne mole of monatomic ideal gas undergoes the process `ArarrB` , as in the given `P-V` diagram . The specific heat for this process is

View SolutionThe internal energy of monatomic ideal gas is `1.5 (MR) T`. One mole of helium is kept in a cylinder of cross-section `8.5 cm^2`. The cylinder is closed by a light frictionless piston. The gas is heated slowly in a process during which a total of `42 J` heat is given to the gas. The temperature of the gas rises by `2 C`. The distance moved by the piston is given as `alpha times 10^(beta)` meter. Find the value of `(alpha+beta)`. [Take universal gas constant `R=(25)/(3) J mol^(-1) K^(-1)`. atmospheric pressure `=100 (kPa)]`
View SolutionThe graph shows variation of internal energy `U` with density `rho` of one mole of an ideal monatomic gas. The process `A B` is a part of rectangular hyperbola. Find the work done (in `J` ) in the process.
'(##CEN_KSR_PHY_JEE_C15_E01_024_Q14##)'
View SolutionA cylinder of cross-section area. A has two pistons of negligible mass separated by distances l loaded with spring of negligible mass. An ideal gas at temperature `T_(1)` is in the cylinder where the springs are relaxed. When the gas is heated by some means its temperature becomes `T_(2)` and the springs get compressed by `(l)/(2)` each . if `P_(0)` is atmospheric pressure and spring constant k=`(2P_(0)A)/(l)`, then find the ratio of `T_(2)` and `T_(1)` .
_S01_124_Q01.png)
View SolutionThe graph shows the `P V` diagram of a process carried out with a certain quantity of oxygen `(gamma=(7)/(5)) .` If `V_(A)=(2)/(3) V_(0)` and `V_(B)=(5)/(12) V_(0)`, then the volume till the gas absorbs beat is `(N)/(12) V_(0)`. Find `N`.
'(##CEN_KSR_PHY_JEE_C15_E01_026_Q16##)'
View SolutionA vessel of volume `V_(0)` is evacuated by means of a piston air pump. One piston stroke captures volume `Delta V=0.2 V_(sigma)`. If the process is assumed to be isothermal, then find the. minimum number of strokes after which pressure in the vessel becomes `((1)/(1.728))` times the initial pressure.
View SolutionThere is `5 g` of a certain diatomic gas in a container closed with a frictionless piston. The gas is.heated for `25 s` by an electric resistor of `50 Omega` built in the container, applying a voltage of `220 V`. While the gas expands at constant pressure, its temperature increases by `250^(circ) C`. The efficiency of the electric heater is `75 %`. What is the molar mass of gas (in g/mol)? Approximate your answer to nearest integer.
'(##CEN_KSR_PHY_JEE_C15_E01_028_Q17##)' figure
View SolutionA quantity of 2 mol of helium gas undergoes a thermodynamic process, in which molar specific heat capacity `C` of the-gas depends on absolute temperature `T`, according to relation: `C=(3 R T)/(4 T_(0))` where `T_(0)` is' initial temperature of gas. It is observed that when temperature is increased, volume of gas first decreases and then increases. The total work done on the gas until it reaches minimum volume is `(gamma)/(8) R T_(0)`. Find `(gamma+delta)`
View Solution100 mol of an ideal monatomic gas undergoes the following thermodynamic process as shown in the figure ( `P-V` or Pressure-Volume plots are shown) `A rarr B:` Isothermal expansion `B rightarrow C` Adiabatic expansion
`C rarr D:` Isobaric compression
`D rarr A:` Isochoric process ,br> The heat transfer along the process `A B` is `9 xx 10^(4) J`. The net work done by the gas during the cycle is `k xx 10^(4) J`. Find `k`, (Take `R=8 (~J) . (K)^(-1) (~mol)^(-1)` )
'(##CEN_KSR_PHY_JEE_C15_E01_030_Q18##)'
View SolutionA cylinder fitted with a spring loaded piston, shown in the figure, contains `0.0 1 (m)^(3)` gas at a pressure of `10^(5) Pa`. The cross-sectional area of the piston is `0.05 m^(2)`. Initially, the spring does not touch the piston but atmospheric pressure of `10^(5) Pa` acts on the piston. The gas is slowly heated till the volume is increased to three times the original value. If the forcé constant of the spring is `25 (kN) / (m)`, calculate the work done (in kJ ) by the gas.
'(##CEN_KSR_PHY_JEE_C15_E01_031_Q19##)'
View SolutionThe figure shows a container having adiabatic walls and a freely movable separator which is highly conducting. The separator divides the cylinder in two equal parts `A` and `B` each containinig 2 mol of ideal monatomic gas at temperature `300 K`. Now a heater is switched on in part `A`. Find the heat supplied (in kJ) by the heater till the pressure in part `A` is doubled. [Take `R=(25)/(3)` SI units]
'(##CEN_KSR_PHY_JEE_C15_E01_032_Q20##)'
View SolutionA cetain quantity of an ideal gas takes up `56 J` of heat in the process `A B` and `360 J` in the process `A C`, as showa in the figure. Whạt is the number of degrees of freedom of the gas?
'(##CEN_KSR_PHY_JEE_C15_E01_033_Q21##)'
View SolutionAs shownin the figure, `0.5 mol` of an ideal gas is kept inside an adiabatic cylinder of length `L` and cross-sectional area `A` closed by massless adiabatic piston. The cylinder is attached with a conducting rod of length `L`, crosssectionail area `(1)/(900) m^(2)` and thermal condactivity `415.5 W` m^(-1) K^(-1)`, whose other end is maintained at `0^(circ) C`. The piston is moved such that the temperature of the gas remains constant at `27^(circ) C`. Find the velocity (in `(mm) / (s)` ) of the piston when it is at beight `L / 2` from the bottom of cylinder. (Rod is well lagged and has negligible heat capacity, `R=8.31 (Jmol ^(-1) K^(-1)` )
'(##CEN_KSR_PHY_JEE_C15_E01_034_Q22##)'
View Solution
QUESTION BANK questions and complete solutions for chapter THERMODYNAMICS of CENGAGE PHYSICS (HINGLISH) of Class 12