Complete Solutions to गणित of chapter सॉल्वड पेपर - 2005 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सॉल्वड पेपर - 2005 |
| CGPET | गणित |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
`|((1+i)(2+i))/((3+i))|` बराबर है
View Solutionमाना `z_(1)` और `z_(2)` समीकरण `z^(2)+az+b=0`, के दो मूल है, z सम्मिश्र संख्या है: पुनः माना मूल बिन्दु `z_(1)` और `z_(2)` एक समबाहु त्रिभुज बनाते है। तब:
View Solutionयदि `-1+sqrt(-3)=re^(itheta)` तब `theta` बराबर है
View Solutionयदि `((1+i)/(1-i))^(x)=1`, तब
View Solution`(1^(3)+2^(3)+3^(3)+ . . . +12^(3))/(1^(2)+2^(2)+3^(2)+ . . . +12^(2))` बराबर है
View Solutionयदि रैखिक समीकरण निकाय
`x+2ay+az=0`
`x+3by+bz=0`
`x+4cy+cz=0`
का एक अशून्य हल है तब a,b,c
View Solutionयदि समीकरणों `x=cy+bz,y=az+cx` तथा क`z=bx+ay` का `x=0,y=0,z=0` के अतिरिक्त एक अन्य हल है तब a,b व c निम्न में से किस सम्बन्ध को संतुष्ट करते है ?
View Solutionयदि `x_(1),x_(2),x_(3)` तथा `y_(1),y_(2),y_(3)` दोनों गुणोत्तर श्रेणी में है जिनके सर्वानुपात समान है तब बिन्दु `(x_(1),y_(1)),(x_(2),y_(2))` व `(x_(3),y_(3))`
View Solution`2^(1//4)*4^(1//8)*8^(1//16)*16^(1//32) . . . Prop` का मान है
View Solutiona के किस मान के लिये समीकरण
`(a^(2)-5a+3)x^(2)+(3a-1)x+2=0` का एक मूल दूसरे मूल का दोगुना होगा
View Solutionयदि समीकरण `(x^(2)-bx)/(ax-c)=(lamda-1)/(lamda+1)` के मूल `alpha` व `beta` इस प्रकार है कि `alpha+beta=0` तब `lamda` का मान है
View Solutionएक छात्र को एक परिक्षा में 13 में से 10 प्रश्नो का उत्तर इस प्रकार देना है कि प्रथम पांच प्रश्नो में से कम - से -कम 4 में प्रश्नो का चयन करना है चयन के तरीको की संख्या है
View Solutionसंख्याओं 2,0,4,3,8 से पांच अंको की कितनी संख्याएं बनायी जा सकती है जबकि अंको की पुनरावृत्ति नहीं हो सकती है ?
View Solution`(sqrt(3)+8sqrt(5))^(256)` के प्रसार में पूर्णांक पदों की संख्या है
View Solution`C_(1)+2C_(2)+3C_(3)+ . . . . +nC_(n)` बराबर है
View Solutionश्रेणी `log_(4)2-log_(8)2+log_(16)2-oo` का योग है
View Solution`|(a,a^(2),1+a^(3)),(b,b^(2),1+b^(3)),(c,c^(2),1+c^(3))|=0` तथा सदिश `(1,a,a^(2)),(1,b,b^(2))` तथा `(1,c,c^(2))` असमतलीय है तब abc का मान है
View Solution`|{:(y+z,x,x),(y,z+x,y),(z,z,x+y):}|` का मान है
View Solutionयदि कोटि 3 के वर्ग आव्यूह A व B इस प्रकार है कि `|A|=-1` तथा `|B|=3` तब `|3AB|` का मान है
View Solutionमाना `A=[(0,0,-1),(0,-1,0),(-1,0,0)]`, तब आव्यूह A के लिए सत्य कथन है
View Solutionयदि `A=[(2,0,0),(0,2,0),(0,0,2)]` हो, तो `A^(5)` बराबर होगा-
View Solution`f(theta)=asintheta+bcostheta` का अधिकतम मान है
View Solutionn भुजा वाले समबहुभुज जिसकी भुजा की लम्बाई a है के अन्त वृत्त तथा परिवृत्त की त्रिज्याओं का योग है
View Solution`(sin70^(@)+cos40^(@))/(cos70^(@)+sin40^(@))` का मान है
View Solutionत्रिकोणमितीय समीकरण `sin^(-1)x=sin^(-1)a` का एक हल है
View Solution`sin6theta+sin4theta+sin2theta=0`, तब `theta` का मान है
View Solutionयदि `DeltaABC` में , `"a cos"^(2)(C )/(2)+"c cos"^(2)((A)/(2))=(3b)/(2)`, तब भुजाएं a,b व c
View Solutionयदि `Agt0,Bgt0` तथा `A+B=(pi)/(3)` तब `tanAtanB` का अधिकतम मान है
View Solutionतीन विभिन्न क्षणों पर सूर्य की किरणों द्वारा बनी h ऊँचाई वाले ऊर्ध्वाधर स्तम्भ की परछाइयों की लम्बाईयाँ क्रमशः h, 2h व 3h है इन तीन क्षणों पर किरणों द्वारा बने उन्नयन कोणों का योग है
View Solution`"tan"^(-1)1/2+"tan"^(-1)1/3` बराबर है
View Solutionउस बिंदु का बिन्दुपथ जिसकी बिंदुओं `(3,0) व `(-3,0)` से दूरियों का अन्तर 4 है है
View Solutionएक त्रिभुज जिसकी शीर्ष `(acost,asint),(bsint,-bcost)` तथा (1,0) है एक प्राचल है के केन्द्रक का बिन्दुपथ है
View Solutionबिंदु `(-2,3)` की रेखा `x-y=5` से दूरी है
View Solutionभुजा a का एक वर्ग x-अक्ष से ऊपर स्थित है तथा एक शीर्ष मूलबिंदु पर स्थित है मूलबिंदु से होकर जाने वाली रेखा धनात्मक x-अक्ष से `alpha(0ltalphalt(pi)/(4))` कोण बनाती है।
मूलबिन्दु से न जाने वाले विकर्ण का समीकरण है
View Solutionरेखाओं `y-x+7=0` तथा `y+2x-2=0` के प्रतिच्छेद बिंदु तथा मूलबिन्दु को मिलाने वाली रेखा का समीकरण है
View Solutionसमीकरण `ax^(2)+2hxy+by^(2)=0` द्वारा निरूपित दो सरल रेखाएं लम्बवत होंगी, यदि
View Solutionयदि समीकरण `x^(2)-2cxy-7y^(2)=0` द्वारा निरूपित रेखायें की प्रवणताओं का योग उनके गुणनफल का चार हो, तब c का मान है
View Solutionयदि दो वृत्त `(x-1)^(2)+y-3)^(2)=r^(2)` तथा `x^(2)+y^(2)-8x+2y+8=0` दो भिन्न बिंदुओं पर प्रतिछ्छेद करते है तब
View Solutionवृत्त `2x^(2)+2y^(2)-2x-5y+3=0` पर `(1,1)` से खींचें गए अभिलम्ब का समीकरण है
View Solutionपरवलय जिसका शीर्ष मोलबिंदु पर व y-अक्ष पर है तथा बिंदु (6,-3) से होकर जाता है का समीकरण है
View Solutionपरवलय के बिंदु `(bt_(1)^(2),2bt_(1))` पर खींची गया अभिलम्ब परवलय को पुनः बिंदु `(bt_(2)^(2),2bt_(2))` पर मिलता है तब
View Solutionयदि रेखा `xcosalpha+ysinalpha=p`, दीर्घवृत्त `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` पर अभिलम्ब है तब
View Solutionदीर्घवृत्त `(x^(2))/(16)+(y^(2))/(b^(2))=1` तथा अतिपरवलय `(x^(2))/(144)-(y^(2))/(81)=1/(25)` की नाभियाँ समान है तब `b^(2)` का मान है
View Solutionअतिपरवलय `9x^(2)-16y^(2)=144` की नाभियाँ है
View Solutionदीर्घवृत्त जिसका केन्द्र मूलबिन्दु पर है की उत्केन्द्रता `1/2` है यदि एक नियता `x=4` हो तब दीर्घवृत्त का समीकरण है
View Solutionयदि एक समतल पर मूलबिन्दु से डाले गए लम्ब की लम्बाई इकाई है तथा इस समतल के दिक् अनुपात `-3,2` व 6 है तब समतल का समीकरण है
View Solutionगोले `x^(2)+y^(2)+z^(2)+4x-2y-6z=155` से समतल `12x+4y+3z=327` की न्यूतम दूरी है
View Solutionरेखा `(x-1)/(3)=y/4=(z+3)/(4)` के समान्तर व् बिंदु `(-1,0,4)` से होकर जाने वाली रेखा तथा बिंदुओं `(2,1,-3)` व् `(-3,1,7)` को मिलाने वाली रेखा के बीच का न्यूनकोण है
View Solutionनिर्देशांक अक्षो के दो निकायों का मूलबिन्दु एक ही है यदि एक समतल मूलबिन्दु से `a,b,c` व् `a',b',c'` दूरी पर उनको काटता है तब
View Solutionयदि एक समतल बिंदु (1,1,1) से होकर जाता है तथा रेखा `(x-1)/(3)=(y-1)/(1)=(z-1)/(1)` के लम्बवत है तब मूलबिन्दु से इस समतल की लम्बवत दूरी है
View Solutionएक रेखा x-अक्ष और z-अक्ष दोनों से `theta` कोण बनाती है यदि यह रेखा y-अक्ष के साथ `beta` कोण इस प्रकार बनाती है कि `sin^(2)beta=3sin^(2)theta`, तब `cos^(2)theta` बराबर है
View Solutionयदि बिंदु `vec(a)` से होकर जाने वाली तथा `vec(b)` के समान्तर रेखा का समीकरण `vec(r )=vec(a)+tvec(b)` है जहां प्राचल है तब बिन्दु `vec(c ) ` से रेखा की लम्बवत दूरी है
View Solutionगोलों `x^(2)+y^(2)+z^(2)+7x-2y-z=13` तथा `x^(2)+y^(2)+z^(2)-3x+3y+4z=8` गोले तथा एक समतल के प्रतिच्छेदन के समान है समतल का समीकरण ही
View Solutionयदि सदिशों `vec(a)=2hat(i)+2hat(j)-hat(k)` तथा `vec(b)=6hat(i)-3hat(j)+2hat(k)` के बीच कोण `theta` है तब
View Solution`vec(a),vec(b),vec( c)` तीन सदिश इस प्रकार है कि `|vec(a)+vec(b)+vec(c )|=0, |vec(a)=1,|vec(b)|=2,|vec(c )|=3`, तब `vec(a)*vec(b)+vec(b)*vec(c )+vec ( c)*vec(a)` का मान है
View Solutionयदि P तथा Q के स्थित सदिश क्रमशः `(hat(i)+3hat(j)-7hat(k))` तथा `(5hat(i)-2hat(j)+4hat(k))` है तब `|vec(PQ)|` का मान है
View Solutionमाना `vec(u)=hat(i)+hat(j),vec(v)=hat(i)-hat(j)` तथा `vec(w)=hat(i)+2hat(j)+3hat(k)`, यदि `hat(n)` एक इकाई सदिश इस प्रकार है कि `vec(u)*hat(n)=0` तथा `vec(v)*hat(n)=0`, तब `|vec(w)*hat(n)|` बराबर है
View Solutionयदि `vec(A)=hat(i)-2hat(j)-3hat(k),vec(B)=2hat(i)+hat(j)-hat(k)` तथा `vec( C)=hat(i)+3hat(j)-2hat(k)` , तब`[vec(a) vec(b) vec(c)]`का मान है
View Solutionएक कण पर दो बल `4hat(i)+hat(j)-3hat(k)` तथा `3hat(i)+hat(j)-hat(k)` कार्यरत है जिससे यह कण `hat(i)+2hat(j)+3hat(k)` से `5hat(i)+4hat(j)+hat(k)` पर विस्थापित हो जाता है बालो द्वारा किया गया कार्य है
View Solutionएक समान्तर षट्फलक जिसकी भुजाएँ `vec(a)=2hat(i)-3hat(j),vec(b)=hat(i)+hat(j)-hat(k)` तथा `vec(c )=3hat(i)-hat(k)` है का आयतन है
View Solutionयदि `vec(a),vec(b),vec(c )` तीन असमतलीय सदिश है तथा `lamda` एक वास्तविक संख्या है तब सदिश `vec(a)+2vec(b)+3vec(c ), lamdavec(b)+4vec(c )` तथा `(2lamda-1)vec(c )` असमतलीय होंगे
View Solution`lim_(xto0)((1-cos2x)sin5x)/(x^(2)sin3x)` का मान है
View Solutionएक फलन `f:N to N` इस प्रकार परिभाषित है कि `f(n)={((n-1)/(2)",जब n एक विषम संख्या है"),((-n)/(2)", जब n एक सम संख्या है"):}` तब है
View Solution`lim_(xto2)(3^(x//2)-3)/(3^(x)-9)` का मान है
View Solutionयदि `f:RtoR` सम्बन्ध `f(x+y)=f(x)+f(y),Aax,yinR` को संतुष्ट करता है तथा `f(1)=7` तब `underset(r=1)overset(n)(Sigma)f(r )` का मान है
View Solutionफलन `cos^(-1)(sinsqrt((1+x)/(2)))+x^(x)` का x सापेक्ष `x=1` पर प्रथम अवकलज है
View Solutionयदि `siny=xsin(a+y)`, तब `(dy)/(dx)` बराबर है
View Solutionx के वे मान जिसके लिए फलन `(sqrt(x)+(1)/(sqrt(x)))^(2)` का x के सापेक्ष अवकलज `3/4` है है
View Solutionयदि `x^(y)=e^(x-y)`, तब `(dy)/(dx)` बराबर है
View Solutionवक्र `y=12x-x^(3)` पर स्थित वे बिन्दु जिन पर प्रवणता शून्य हो है
View Solutionयदि `f(x) = x^(n)` तो `f(1)-(f'(1))/(1!)+(f''(1))/(2!)-(f'''(1))/(3!)+......+((-1)^(n)f^('''''''''....("n times"))(1))/(n!)` का मान होगा
View Solutionफलन `f(x)=2x^(3)-21x^(2)+36x-20` का निम्निष्ठ मान है
View Solutionयदि `f(x)=2x^(3)-9ax^(2)+12a^(2)x+1` जब `agt0` के उच्चिष्ठ तथा निम्निष्ठ मान क्रमशः p व q पर इस प्रकार है
कि `p^(2)=q`, तब a का मान है
View Solution`int (dx)/(1-x^(2))` का मान है
View Solution`lim_(nto oo)underset(r=1)overset(n)(Sigma)1/n e^(r//n)` का मान है
View Solution`int (cos2x-1)/(cos2x+1)dx` का मान है
View Solutionमाना फलन f इस प्रकार है कि `f(-x)=-f(x),AA x in R` तथा `int_(0)^(1)f(x)dx=5`, तब `int_(-1)^(0)f(t)dt` बराबर है
View Solutionयदि `f(y)=e^(y),g(y)=y,y gt0` तथा `F(t)=int_(0)^(t)f(t-y)*g(y)dy`, तब
View Solutionयदि `x`-अक्ष, वक्र `y=f(x)` तथा रेखाओ `x=1,x=b` द्वारा सभी `b gt 1` के लिए परिबद्ध क्षेत्रफल `sqrt(b^(2)+1)-sqrt(2)` के बराबर है, तब `f(x)` होगा-
View Solutionमाना `f(x)` एक फलन इस प्रकार है कि `f'(x)=f(x)` तथा `f(0)=1` तथा `g(x)` एक फलन है जो सम्बन्ध `f(x)+g(x)=x^(2)` को संतुष्ट करता है समाकलन `int_(0)^(1)f(x)g(x)dx` का मान है
View Solution`int_(-1)^(0)(dx)/(x^(2)+2x+2)` का मान है
View Solutionवक्र कुल `y=Ax+A^(3)` की अवकलन समीकरण की घात है
View Solutionउन सभी परवलयो जिनका अक्ष x-अक्ष है के अवकलन समीकरण की कोटि व घात क्रमशः है
View Solutionअवकल समीकरण `ydx-xdy=x^(2)ydx` का हल है
View Solutionअवकलन समीकरण `(1+y^(2))+(x-e^(tan^(-1)y))(dy)/(dx)=0` का हल है
View Solution`(x+y-1)dx+(2x+2y-3)dy=0` का हल है
View Solutionवक्र कुल `x^(2)+y^(2)-ay=0` जहाँ a एक स्वच्छ अचर है की अवकल समीकरण है
View Solutionअवकलन समीकरण `cosx(dy)/(dx)+ysinx=1` का हल है
View Solutionअवकलन समीकरण `ydx+(x+x^(2)y)dy=0` का हल है
View Solutionदिया है, `P(AuuB)=5/6,P(AnnB)=1/3` तथा `P(B)=1/2`, तब `P(A)` का मान है
View Solutionएक द्विपद बंटन के चर के माध्य तथा प्रसरण क्रमशः 4 व 2 है तब `P(X=1)` का मान है
View Solutionयदि A और B दो समुच्चय है तब `(AnnB)'=`
View Solutionयदि y की x पर तथा x की y पर समाश्रयण रेखाएं x-अक्ष की धनात्मक दिशा के साथ `30^(@)` तथा `60^(@)` का कोण बनाती है तब x तथा y के बीच सहसम्बन्ध गुणांक है
View Solutionयदि x व y दो सवतंत्र चर है तब सहसम्बन्ध गुणांक है
View Solutionसमीकरण `x^(3)-3x+4=0` का केवल एक वास्तविक मूल है मिथ्या स्थिति के नियम से इसका पहला सन्निकट मूल `(-3,-2)` अंतराल में है
View Solutionयदि न्यूटन - राफ्सन विदित द्वारा समीकरण `f(x)=0` के दो क्रमागत मूल a व a+h प्राप्त होते है तब h का मान है
View Solutionयदि `2a+3b+6c=0` तब समीकरण `ax^(2)+bx+c=0` का कम से कम एक मूल निम्न अंतराल में होगा
View Solutionयदि f(s) केवल `x=0,1/3,2/3,1` पर ज्ञात हो, तो `int_(0)^(1)f(x)dx` का सन्निकट मान निकालने के लिए नियम में से किसका प्रयोग किया जा सकता है
View Solutionछायांकित भाग निम्न में से किसके द्वारा प्रदर्शित है
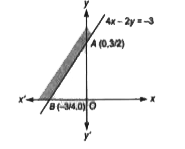
View Solutionछायांकित भाग निम्न में से किसके द्वारा प्रदर्शित है
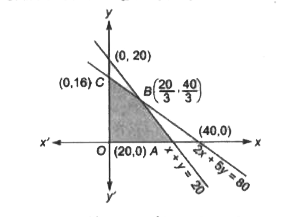
View Solution
गणित questions and complete solutions for chapter सॉल्वड पेपर - 2005 of CGPET PREVIOUS YEAR PAPERS MATHS (HINDI) of Class 12