Complete Solutions to EXERCISE of chapter দ্বিতীয় ক্রমের অন্তরকলেজ of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | দ্বিতীয় ক্রমের অন্তরকলেজ |
| CHHAYA PRAKASHINI | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
সঠিক উত্তরটি নির্বাচন করো
`y = root(3)(x^2)` হলে `(d^2y)/dx^2` =
View Solution`y^2 = 4ax` হলে `(d^2y)/dx^2` =
View Solution`y = cos^2x` হলে `[(d^2y)/dx^2]_(x = pi/4)`
View Solutionযদি `f(x) = x^(2/3)`হয়, তবে-
View Solution`r = e^-(mtheta )`হলে `(d^2r)/(d theta^2)` - এর মান হবে-
View Solution`y = tanx` হলে `(d^2y)/(dx^2)` =
View Solution`f(x) = log(cosx)` হলে `(F'')(x)` =
View Solution`f(x) = sin(x/2)` হলে `f''(pi)` =
View Solution`f(x) = log(3x+1)` হলে `f ''(1)` =
View Solution`y=2^(3-2x)` হলে `(d^2y)/dx^2` =
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `x`-এর সাপেক্ষে দ্বিতীয়ক্রমের অন্তরকলজ বা অবকল সহগ নির্ণয় করো : `x^5-6x`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `x`-এর সাপেক্ষে দ্বিতীয়ক্রমের অন্তরকলজ বা অবকল সহগ নির্ণয় করো : `cotx`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `x`-এর সাপেক্ষে দ্বিতীয়ক্রমের অন্তরকলজ বা অবকল সহগ নির্ণয় করো : `log(x^2-4)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `x`-এর সাপেক্ষে দ্বিতীয়ক্রমের অন্তরকলজ বা অবকল সহগ নির্ণয় করো : `tan^-1x`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` নির্ণয় করো : `y = log(sinx)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` নির্ণয় করো :` y = 2sinxcosx` -এর `x = 0` -তে
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` নির্ণয় করো : `y = 10^(2-3x)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` নির্ণয় করো : `y = sin^3x`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` নির্ণয় করো :`y = x^2logx^2` -এর `x = 1` -এ
View Solutionসংক্ষিপ্ত উত্তরধর্মী
নিম্নলিখিত প্রতিক্ষেত্রে `y_2` নির্ণয় করো :`y = cos3xsin4x`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `y_2` নির্ণয় করো : `y = x/(2x-3)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `y_2` নির্ণয় করো : `y = log((a-x)/(a+x))`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `y_2` নির্ণয় করো :` y = e^(4x)cos3x`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `y_2` নির্ণয় করো : `y = log(ax+x^2)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `y_2` নির্ণয় করো : `y = xe^(1/x)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `y_2` নির্ণয় করো : `y = sin^2x`
View Solution`(x^2/a^2)-(y^2/b^2) = 1` হলে `((d^2y)/dx^2)` এর মান নির্ণয় করো
View Solution`x^2+y^2 = 25` এর `x=0` বিন্দুতে `(d^2y)/(dx^2)` এর মান নির্ণয় করো
View Solution`y = tan^-1(secx+tanx)` হলে `x = (pi/4)` বিন্দুতে `(d^2y)/(dx^2)` এর মান নির্ণয় করো
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` এর মান নির্ণয় করো : `x = t, y = t^2`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` এর মান নির্ণয় করো : `x = at^2, y = 2at`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` এর মান নির্ণয় করো : `y=acostheta , x = bsintheta`
View Solution`x = Acos nt+Bsin nt` (`A,B,n`ধ্রুবক) হলে দেখাও যে, `(d^2x)/(dt^2) + n^2x = 0`
View Solutionঘনফল নির্ণয় করো : `x^2+2`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `f''(x)` নির্ণয় করো : `f(x) = 1/(x^2-4)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `f''(x)` নির্ণয় করো : `f(x) = sinxsin2xsin3x`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `f''(x)` নির্ণয় করো : `f(x) = e^xsin^2x`
View Solutionঘনফল নির্ণয় করো : `x^2+2`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` এর মান নির্ণয় করো : `tany = (sqrt(1+x^2)-1)/x`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` এর মান নির্ণয় করো : `y = tan (x+y)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` এর মান নির্ণয় করো :` sinx + cosy = 1`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `(d^2y)/(dx^2)` এর মান নির্ণয় করো :` x^py^q = (x+y)^(p+q)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `y_2` এর মান নির্ণয় করো :` x = acos^3theta , y = asin^3theta`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `y_2` এর মান নির্ণয় করো :` x = a(theta+sintheta), y = a(1-costheta)`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `y_2` এর মান নির্ণয় করো : `x = a(t+(1/t)), y = a(t-(1/t))`
View Solutiona, b, c এর মান নির্ণয় করো।
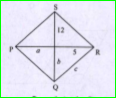
View Solutiona, b, c এর মান নির্ণয় করো।

View Solutionমান নির্ণয় করো : `sin (2theta+45^@)=cos (30^@-theta)` হলে `theta`=?
View Solutionপ্রদত্ত চিত্র থেকে x এর মান নির্ণয় করো।
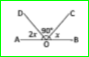
View Solution`y^3 = x^2+y^2` এর `y=1` বিন্দুতে `(d^2y)/(dx^2)` -এর মান নির্ণয় করো
View Solution`y = x/(x^2-x-2)` -এর `x=1` বিন্দুতে `y_2` এর মান নির্ণয় করো
View Solution`y = xsinx` হলে প্রমাণ করো যে,
` x^2((d^2y)/(dx^2))-2x((dy)/(dx))+(2+x^2)y = 0`
View Solution`y = ae^(mx)+bcosmx` হলে প্রমাণ করো যে,
`(d^2y)/(dx^2)+m^2y = 2am^2e^(mx)`
View Solution`y = e^-x(cosx+sinx)` হলে দেখাও যে, `y_2+2y_1+2y = 0`
View Solution`y = e^x(sinx+cosx)` হলে দেখাও যে, `((d^2y)/(dx^2))-2((dy)/(dx))+2y = 0`
View Solution`y = x^3log(1/x)` হলে প্রমাণ করো যে,` xy_2-2y_1+3x^2=0`
View Solution`y = log(x+sqrt(a^2+x^2))`হলে দেখাও যে, `(a^2+x^2)y_2+xy_1 = 0`
View Solution`y = [log(x+sqrt(x^2+1))]^2` হলে দেখাও যে, `(1+x^2)((d^2y)/(dx^2))+x((dy)/(dx)) = 2`
View Solution`y = secx+tanx` হলে দেখাও যে, `y_2-yy_1 = 0`
View Solution`y = 3cos(logx)+4sin(logx)` হলে দেখাও যে, `x^2y_2+xy_1+y = 0`
View Solutionযদি `y^2=xz` হয় তবে প্রমাণ করো যে, `(x^2-y^2+z^2) / (x^(-2)-y^(-2)+z^(-2) ) =y^4`
View Solution`y = x^2cosx` হলে দেখাও যে,
`x^2y_2-4xy_1+(x^2+6)y = 0`
View Solution`cosx = ycos(a+x)` হলে প্রমাণ করো যে, `(d^2y)/(dx^2) = 2sinasec^2(a+x)tan(a+x) `
View Solution`y = sin(logx)` হলে দেখাও যে, `x^2y_2+xy_1+y = 0`
View Solution`Sin^-1x = logy` হলে দেখাও যে, `(1-x^2)y_2 - xy_1 - y = 0`
View Solution` y = cos(cosx) ` হলে দেখাও যে, `y_2 - y_1.cotx + ysin^2 x =0`
View Solution`y = sin^-1 x` হলে দেখাও যে, `(1 - x^2)y_2 - xy_1 = 0`
View Solution` y = (sin^-1x)/( sqrt(1-x^2))` হলে দেখাও যে,
`(1-x^2) (d^2y)/dx^2 -3x (dy)/dx - y =0`
View Solution`x/y = (a+2)/(a-2)` হলে দেখাও যে, `(x^2-y^2)/(x^2+y^2)` = `4a/(a^2+4)`
View Solution`y = (tan^-1x)^2` হলে দেখাও যে,
`(1 + x^2)^2y_2 + 2x(1 +x^2)y_1 -2 = 0`
View Solution`y = e^(msin^-1x) (-1 le x le 1)` হলে প্রমাণ করো যে,
`(1-x^2)(d^2y)/dx^2 -x (dy)/dx = m^2y`
View Solution`y = cos(msin^-1x)` হলে দেখাও যে,
`(1 - x^2)y_2-xy_1 + m^2y = 0`
View Solution. `y = sin(2sin^-1x)` হলে দেখাও যে, `(1 - x^2)(d^2y)/dx^2 = x(dy)/dx - 4y`
View Solution` y = 3e^(2x) + 2e^(3x)` হলে দেখাও যে, `y_2 - 5y_1 + 6y = 0`
View Solution`y = (logx)/x` হলে দেখাও যে, `[(d^2y)/dx^2]_(x=1) =-3`
View Solution`x^2 + y^2 = a^2` হলে দেখাও যে,
` ((1 + y_1^2)^(3/2))/y_2 = – a `
View Solutionযদি `y = x^3` এবং` k = ((d^2y)/dx^2)/[1 + ((dy)/dx)^2]^(3/2)` হয়, তবে `(1,1)` বিন্দুতে`k`-এর মান নির্ণয় করো।
View Solution`tantheta=1` হলে, `(8Sintheta+5Costheta)/(Sin^3theta-2Cos^3theta+7Costheta)`-এর মান নির্ণয় করো।
View Solution`a:b= b:c` হলে দেখাও যে `(a+b)^2 : (b+c)^2=a:c`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `a` ও `b` অপনয়ন করো: `y = alogx + b`
View Solutionনিম্নলিখিত প্রতিক্ষেত্রে `a` ও `b` অপনয়ন করো:`xy = ax^3 + b`
View Solutionনিম্নলিখিত দ্বিঘাত সমীকরণের বীজদ্বয়ের প্রকৃতি নির্ণয় করো: `2(a^2+b^2)y^2+2(a+b)y+1=0`
View Solutionদীর্ঘ উওরধর্মী
`y = sqrt(x+1)-sqrt(x-1)` হলে দেখাও যে,
`((x^(2)-1)(d^(2)y)/(dx^(2))+(x(dy)/(dx))=(1/4)y`
View Solutionযদি, `y = A(x+sqrt(x^(2)-1))^(n)+B(x- sqrt(x^(2)-1))^(n)` হয়, তবে দেখাও যে,` (1-x^(2))(d^(2)y)/(dx^(2))-x((dy)/(dx))+n^(2)y=0`
View Solution`y= (cos^(-1)x)^(2)` হলে দেখাও যে, `(1-x^(2))y_2-xy_1-2=0` অতঃপর `y_2` এর মান নির্ণয় করো, যখন `x=0`
View Solution`y=e^(x)logx` হলে দেখাও যে,
`xy_2-(2x-1)y_1+(x-1)y=0`
View Solution`y^(2)=4ax` অধিবৃত্তে প্রমাণ করো যে, `(d^(2)y)/(dx^(2)).(d^(2)x)/(d^(2)y)= -(2a)/(y^(3))`
View Solution`x=cost` এবং `y=logt` হলে প্রমাণ করো যে, `t=(pi)/(2)` তে `(d^(2)y)/(dx^(2))+((dy)/(dx))^(2)=0`
View Solution`t` একটি প্যারামিটার এবং `x=t^(2)+2t`, `y=t^(3)-3t` হলে দেখাও যে, `(d^(2)y)/(dx^(2)) = 3/(4(t+1))`
View Solution`t` একটি প্যারামিটার এবং `x=t^(2)+2t`, `y=t^(3)-3t` হলে দেখাও যে, `(d^(2)y)/(dx^(2)) = (3)/(4(t+1))`
View Solution`y = ae^(tsqrt(2))+be^(-tsqrt(2))` এবং `x=sin t` হলে প্রমাণ করো যে,
`(1-x^(2))(d^(2)y)/(dx^(2))-x((dy)/(dx))= 2y`
View Solution`S=(1)/(2)log((1+t)/(1-t))` হলে প্রমাণ করো যে,
`((ds)/(dt)).((dt)/(ds))=1`
View Solution`s=(1)/(2)log((1+t)/(1-t))` হলে প্রমাণ করো যে,
`(d^(2)s)/(dt^(2))=((ds)/dt)^(3).(d^(2)t)/(ds^(2))`
View Solution`x= (1)/(z)` এবং y=f(x) হলে দেখাও যে,
`(d^(2)f)/(dx^(2))= 2z^(3)((dy)/(dz))+z^(4)(d^2y)/(dz^(2))`
View Solution`y=e^xlog x` হলে দেখাও যে,
`xy_2-(2x-1)y_1+(x-1)y=0`
View Solution`logx=z` ধরে দেখাও যে, `x^(2)(d^(2)y)/(dx^(2))= (d^(2)y)/(dz^(2))-(dy)/(dz)`
View Solution`x= Ae^(-(kt)/2)cos(pt+epsilon) `হলে এবং `A,k,p, epsilon` ধ্রুবক হলে, দেখাও যে, `(d^(2)x)/(dt^2)+k(dx)/(dt)+n^(2)x=0`,যেখানে `n^(2)=p^(2)+(1/4)k^(2)`
View Solution`2x=y^(1/5)+y^(-(1/5)) ` হলে প্রমাণ করো যে, `(x^(2)-1)y2+xy1=25y[ `যেখানে`,yr=(d^(r)y)/(dx^(r))]`
View Solution`y^(4)+5xy+y=2` হলে `(dy/dx)` ও `(d^(2)y)/(dx^(2))` এর মান নির্ণয় করো, যখন x=0, y=1
View Solutionযদি `F(x) =f(x)phi(x)`এবং `f'(x)phi'(x)=0,` (a ধ্রুবক) হয়, তাহলে দেখাও যে,
`((F''))/F= ((F''))/f+phi"/phi+2a/fphi` `[`যেখানে` _= (d^(2))/(dx^(2)), '_= (d/dx), F(x) !=0]`
View Solution
EXERCISE questions and complete solutions for chapter দ্বিতীয় ক্রমের অন্তরকলেজ of CHHAYA MATHS (BENGALI) of Class 12