Complete Solutions to Example of chapter Differentiation of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | Differentiation |
| CHETANA PUBLICATION | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Differentiate w. r. t. x : `(x^3 - 2x - 1)^5`
View SolutionDifferentiate w. r. t. x : `(2x^frac{3}{2} - 3x^frac{4}{3} - 5)^frac{5}{2}`
View SolutionDifferentiate w. r. t. x : ` sqrt (x^2+ 4x -7)`
View SolutionDifferentiate w. r. t. x : ` sqrt (x^2 + sqrt( x^2 + 1))`
View SolutionDifferentiate w. r. t. x : ` frac{3}{5 root(3)((2 x^2 -7x -5)^5)}`
View SolutionDifferentiate w. r. t. x : `{sqrt (3x - 5) - frac{1}{ sqrt (3x - 5) }}^5`
View SolutionDifferentiate the following w. r. t. x : cos( `x^2` + `a^2`)
View SolutionDifferentiate the following w. r. t. x : `sqrt ( e^(3x+2) +5 )`
View SolutionDifferentiate the following w. r. t. `x : log(tan frac{x}{2})`
View SolutionDifferentiate the following w. r. t. x : `sqrt (tan sqrt x)`
View SolutionDifferentiate the following w. r. t. x : `cot^3 (log x^3)`
View SolutionDifferentiate the following w. r. t. x : `5^(sin^3 x + 3)`
View SolutionDifferentiate the following w. r. t. `x : cosec ( sqrt cosx`)
View SolutionDifferentiate the following w. r. t. x : log [cos ( `x^3` - 5)]
View SolutionDifferentiate the following w. r. t. x : `e^(3sin ^ 2 x- 2 cos^2 x)`
View SolutionDifferentiate the following w. r. t. `x : cos^2 [log ( x^2 + 7)]`
View SolutionDifferentiate the following w. r. t.` x : tan[ cos (sin x)]`
View SolutionDifferentiate the following w. r. t. `x : sec [ tan (x^4 + 4)]`
View SolutionDifferentiate the following w. r. t. `x : e^(log ( (log x)^2 - log x^2) `
View SolutionDifferentiate the following w. r. t. `x : sin ( sqrt sin (sqrt x))`
View SolutionDifferentiate the following w. r. t. `x : log[sec(e^(x^2))]`
View SolutionDifferentiate the following w. r. t. `x : log ( log x^2)`
View SolutionDifferentiate the following w. r. t. x : `[ log (log (log x))]^2`
View SolutionDifferentiate the following w. r. t. x : `sin^2``x^2` -`cos^2``x^2`
View SolutionDifferentiate the following w. r. t. `x : (x^2 + 4x +1)^3 + (x^3 -5x -2)^4`
View SolutionDifferentiate the following w. r. t. `x : (1+4x)^5 + (3 + x - x^2)^8`
View SolutionDifferentiate the following w. r. t. x : `frac{x}{sqrt (7-3x)}`
View SolutionDifferentiate the following w. r. t. x : `frac{(x^3-5)^5}{(x^3+3)^3}`
View SolutionDifferentiate the following w. r. t. x : `(1+sin^2 x)^2(1+cos^2 x)^3`
View SolutionDifferentiate the following w. r. t. `x : sqrt cosx + sqrt cos (sqrt x)`
View SolutionDifferentiate the following w. r. t. `x : log(sec 3x + tan 3x)`
View SolutionDifferentiate the following w. r. t.` x : tan[ cos (sin x)]`
View SolutionDifferentiate the following w. r. t. x : cot `(frac{log x}{2})` - log `(frac{cot x}{2})`
View SolutionDifferentiate the following w. r. t. x : `frac{e^(2x) - e^(-2x)}{e^(2x) + e^(-2x)}`
View SolutionDifferentiate the following w. r. t. x :`frac{e^sqrt x + 1}{e^sqrt x - 1}`
View SolutionDifferentiate the following w. r. t.` x :log[tan^3x. sin^4x.(x^2 +7)^7]`
View SolutionDifferentiate the following w. r. t. x :`log ( sqrt [frac{1 - cos 3x}{1 +cos 3x}])`
View SolutionDifferentiate the following w. r. t. `x :log ( sqrt [frac{1 + cos frac{5x}{2}}{1 - cos frac{5x}{2}}])`
View SolutionDifferentiate the following w.r.t.x: log √( 1- sinx )/( 1 +sinx )
View SolutionDifferentiate the following w. r. t. `x :log [ 4^(2x) (frac{x^2 + 5}{sqrt (2x^3 -4)})^(frac{3}{2})]`
View SolutionDifferentiate the following w. r. t. ` x :log [e^(x^2) (5-4x)^((frac{3}{2})}/{root (3)(7-6x)}]`
View SolutionDifferentiate the following w. r. t. `x :log [ frac{ a^cos x}{(x^2 - 3)^3 log x}]`
View SolutionDifferentiate the following w. r. t. x : y= `25^ (log_{5}(secx))` - `16^ (log_{4} (tan x))`
View SolutionDifferentiate the following w. r. t. x : `frac{(x^2 + 2)^4}{sqrt ( x^2 -5)}`
View SolutionA table of values of f, g, f' and g' is given:
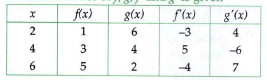 . If r(x) = f[g(x)], find r'(2)
. If r(x) = f[g(x)], find r'(2)
View SolutionA table of values of f, g, f' and g' is given:
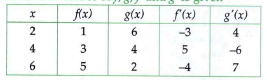 . If R(x) = g[3+ f(x)] , find r'(4)
. If R(x) = g[3+ f(x)] , find r'(4)
View SolutionA table of values of f, g, f' and g' is given:
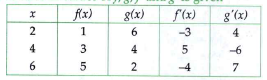 . If s(x) = f[9- f(x)], find s'(4)
. If s(x) = f[9- f(x)], find s'(4)
View SolutionA table of values of f, g, f' and g' is given:
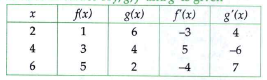 . If S(x) = g[g(x)], find S'(6)
. If S(x) = g[g(x)], find S'(6)
View SolutionAssume that `f'(3) = -1, g'(2) = 5, g(2) = 3 and y=f[g(x)]`, then `[dy/ dx]` at x=2 = ?
View SolutionIf `h(x)` = `sqrt(4f(x) + 3g(x)` , `f(1) = 4, g(1) =3, f'(1) =3, g'(1) = 4`, find `h'(1)`
View SolutionFind the x-coordinates of all the points on the curve `y=sin 2x - 2sin x`, 0`le` x `<` 2`pi`
View SolutionSolve the following: `f(x) = -x` for -2`le` x `<` 0,
= 2x for 0`le` x`le` 2,
=`frac{18-x}{4}` for 2`<`x`le` 7,
g(x) = 6-3x, 0`le` x`<` 2,
=`frac{2x-4}{3}` , 2`le` x `<` 7.
Let u(x)= f[g(x)], v(x)=g[f(x)] and w(x)=g[g(x)]
Find each derivative at x=1, if it exists,
i.e., find the u'(1), v'(1) and w'(1). If it doesn't exist, then explain why?
View SolutionSuppose that the function f and g and their derivatives w.r.t. x have the following values at x=0 and x=1.
 . The derivative of `f[g(x)]` w.r.t. x at `x=0 ` is _____
. The derivative of `f[g(x)]` w.r.t. x at `x=0 ` is _____
View SolutionSuppose that the function f and g and their derivatives w.r.t. x have the following values at x=0 and x=1.
 . The derivative of g[f(x)] w.r.t. x at x=0 is _____
. The derivative of g[f(x)] w.r.t. x at x=0 is _____
View SolutionSuppose that the function f and g and their derivatives w.r.t. x have the following values at x=0 and x=1.
 . The value of `[d/dx [x^10 + f(x)]^(-2)]` at `x= 1` is _____
. The value of `[d/dx [x^10 + f(x)]^(-2)]` at `x= 1` is _____
View SolutionSuppose that the function f and g and their derivatives w.r.t. x have the following values at x=0 and x=1.
 . The derivative of `f[x + g(x)]` w.r.t. x at `x=0` is _____
. The derivative of `f[x + g(x)]` w.r.t. x at `x=0` is _____
View SolutionFind the derivative of the fuction y=f(x) using the derivative of the inverse function x= `f^(-1)` (y) in the following: y= `sqrt x`
View SolutionFind the derivative of the function `y=f(x)` using the derivative of the inverse function `x= f^(-1)` (y) in the following: y= `sqrt (2- sqrt x)`
View SolutionFind the derivative of the function `y=f(x)` using the derivative of the inverse function `x= f^(-1) (y)` in the following: `y= root (3)( x-2)`
View SolutionFind the derivative of the function `y=f(x)` using the derivative of the inverse function `x= f^(-1) (y)` in the following: `y= log ( 2x-1)`
View SolutionFind the derivative of the function `y=f(x)` using the derivative of the inverse function `x= f^(-1)` (y) in the following: `y= 2x+3`
View SolutionFind the derivative of the function `y=f(x)` using the derivative of the inverse function `x= f^(-1)` (y) in the following: `y= e^x - 3`
View SolutionFind the derivative of the function `y=f(x)` using the derivative of the inverse function `x= f^(-1)` (y) in the following: `y= e^ (2x-3)`
View SolutionFind the derivative of the function `y=f(x)` using the derivative of the inverse function `x= f^(-1) (y)` in the following: `y= log_(2) frac{x}{2}`
View SolutionFind the derivative of the inverse function of the following: `y=` `x^2` `e^x`
View SolutionFind the derivative of the inverse function of the following: `y= x cos x`
View SolutionFind the derivative of the inverse function of the following: `y= x` `7^x`
View SolutionFind the derivative of the inverse function of the following: `y= x^2 + log x`
View SolutionFind the derivative of the inverse function of the following: `y= x log x`
View SolutionFind the derivative of the inverse of the following functions, and also find their value at the points indicated against them. `y=x^5 + 2x^3 + 3x`, at `x=1`
View SolutionFind the derivative of the inverse of the following functions, and also find their value at the points indicated against them. `y=e^x +3x + 2`, at `x=0`
View SolutionFind the derivative of the inverse of the following functions, and also find their value at the points indicated against them. `y=3x^2 + 2 log x^3`, at `x=1`
View SolutionFind the derivative of the inverse of the following functions, and also find their value at the points indicated against them. `y= sin (x-2) + x^2`, at `x=2`
View SolutionIf `f(x) = x^3 + x -2`, find `(f^(-1))' (0)`
View SolutionUsing derivative, prove `tan^(-1) x + cot^(-1) x = frac{pi}{2}`
View SolutionUsing derivative, prove `sec^(-1) x + cosec^(-1) x = frac{pi}{2}`
View SolutionDifferentiate the following w.r.t. x: `tan^(-1) (log x)`
View SolutionDifferentiate the following w.r.t x : `y= cosec^(-1)(e^(-x))`
View SolutionDifferentiate the following w.r.t. `x: cot^(-1) (x^3)`
View SolutionDifferentiate the following w.r.t `x: cot^(-1) (4^x)`
View SolutionDifferentiate the following w.r.t. `x: tan^(-1) (sqrt x)`
View SolutionDifferentiate the following w.r.t. `x: sin^(-1) (sqrt (frac {1+ x^2}{2}))`
View SolutionDifferentiate the following w.r.t. `x: cos^(-1) (1-x^2)`
View SolutionDifferentiate the following w.r.t. `x: sin^(-1)` (`x^(3/2)`)
View SolutionDifferentiate the following w.r.t. `x:` `cos^3` [`cos^(-1)` (`x^3`)]
View SolutionDifferentiate the following w.r.t. `x:` `sin^4` [`sin^(-1)` (`sqrt x`)]
View SolutionDifferentiate the following w.r.t. `x: cot^(-1) [ cot(e^(x^2))]`
View SolutionDifferentiate the following w.r.t. `x: cosec^(-1) (frac{1}{cos (5^x)})`
View SolutionDifferentiate the following w.r.t. `x: cos^(-1) (sqrt ( frac {1+cos x} {2}))`
View SolutionDifferentiate the following w.r.t. `x: cos^(-1) (sqrt ( frac {1- cos (x^2)} {2}))`
View SolutionDifferentiate the following w.r.t. `x: tan^(-1) (frac {1- tan (x/2)} {1+ tan (x/2)})`
View SolutionDifferentiate the following w.r.t `x: cosec^(-1) (frac {1} {4 cos^3 (2x) - 3 cos(2x)})`
View SolutionDifferentiate the following w.r.t. `x: tan^(-1) (frac {1+ cos (x/3)} {sin (x/3)})`
View SolutionDifferentiate the following w.r.t. `x: cot^(-1) (frac {sin 3x} {1+cos 3x}) `
View SolutionDifferentiate the following w.r.t. `x: tan^(-1) (frac {cos 7x} {1+sin 7x}) `
View SolutionDifferentiate the following w.r.t. `x: tan^(-1) (sqrt(frac {1+ cos x} {1- cos x}))`
View SolutionDifferentiate the following w.r.t. `x: tan^(-1) (cosec x + cot x)`
View SolutionDifferentiate the following w.r.t x: `sin^(-1)` (`frac { 4 sin x + 5 cos x}{sqrt 41`)
View SolutionDifferentiate the following w.r.t x: `cos^(-1)` (`frac { `sqrt 3` cos x - sin x}/{2}')
View SolutionDifferentiate the following w.r.t x: `sin^(-1)` (`frac { cos sqrt x`+ sin `sqrt x`}/{`sqrt 2`}')
View Solution
Example questions and complete solutions for chapter Differentiation of CHETANA PUBLICATION of Class 12