Complete Solutions to EXERCISE of chapter PROBABILITY DISTRIBUTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY DISTRIBUTIONS |
| CHETANA PUBLICATION | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Let X represent the difference between number of heads and number of tails obtaines when a coin is tossed 6 times.What are the possible values of X?
View SolutionAn urn contains 5 red and 2 black balls.Two balls are drawn at random.X denotes number of black balls drawn.What are the possible values of X?
View SolutionState which of the following are not the probability mass function of a random variable.Give reasons for your answer.(1)

View SolutionState which of the following are not the probability mass function of a random variable.Give reasons for your answer.(2)

View SolutionState which of the following are not the probability mass function of a random variable.Give reasons for your answer.(3)
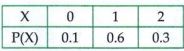
View SolutionState which of the following are not the probability mass function of a random variable.Give reasons for your answer.(5)
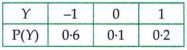
View SolutionState which of the following are not the probability mass function of a random variable.Give reasons for your answer.(6)

View SolutionFind the probability distribution of (i)Number of heads in two tosses of a coin?
View SolutionFind the probability distribution of (iii)Number of heads in four tosses of a coin?
View SolutionFrom a lot of 30 nulbs which include 6 defectives,a sample of 4 bulbs is drawn at random with replacement.Find the probability distribution of the number of defective bulbs.
View SolutionA random variable X has the following probability distribution find mean of x:

View SolutionFind expected value and variance of X,where X is number obtained on uppermost face when a fair die is thrown.
View SolutionTwo dice are thrown simultaneously.If X denotes the number of sixes,find the expectation of X.
View SolutionTwo numbers are selected at random(without replacement) from the first six positive integers.Let X denote the large of the two numbers obtaines.Find E(X).
View SolutionLet X denote the sum of the numbers obtained when two fair dice are rolled.Find the standard deviation of X.
View SolutionA class has 15 students whose ages are 14,17,15,14,21,17,19,20,16,18,20,17,16,19 and 20 years.One student is selected in such a manner that each has the same chance of being chosen and the age X of the selected student is recorded.What is the probability distribution of the random variable X?Find mean,variance and standard deviation of X.
View SolutionIdentify the random variable as either discrete or continuous in each of the following.Write down the range of it.(v)A highway safety group is interested in studying the speed (in Km/hr) of a car at a check point.
View SolutionThe probability distribution of discrete r.v.X is as follows:- Find (i) P(`Xlt=4`),(ii) P(`2ltXlt4`), (iii)P(`Xgt=3`).

View SolutionThe following is probability distribution of random variable X. Values of X: 0 1 2 3 4 5 6 7 8 P(X): a 3a 5a 7a 9a 11a 13a 15a 17a Determine the value of k, if a= 1/k .
View SolutionThe following is probability distribution of random variable X.determine k .
View SolutionThe following is probability distribution of random variable X.Find the probability that (iii)X is odd.

View SolutionThe pmf of r.v X is given by `P(X=x)=(^5C_x)/(2^5)`,for x=0,1,2,3,4,5=0,otherwise Then show that `P(Xlarr2)=P(Xge3)`
View SolutionIn the pmf of r.v.X.Find a and obtain cdf of X.
View SolutionA fair coin is tossed 4 times.Let X denotes the number of heads obtained.Write down the probability distribution of X.Also find the formula for pmf of X.
View SolutionFind the probability distribution of the number of successes in two tosses of a die,where a success is defines as(i)number greater than 4
View SolutionA random variable X has the following probability distribution.Determine (ii)`P(X>6)`

View SolutionA random variable X has the following probability distribution. Determine P( 0 < x < 3 )
View SolutionThe following is cdf of r.v.X.Find pmf of X and (i)`P(1leXle2)`

View SolutionFind the expected value,variance and standard deviation of r.v.X whose pmf are given below.(i)

View SolutionFind the expected value,variance and standard deviation of r.v.X whose pmf are given below.(iii)
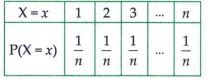
View SolutionFind the expected value,variance and standard deviation of r.v.X whose pmf are given below.(iv)

View SolutionTwo cards are randomly frawn,with replacement,from a well shuffled deck of 52 playing cards.Find the probability distribution of the number of aces drawn.
View SolutionThe probability distribution of X as follows.Find (i)k

View SolutionThe probability distribution of X as follows.Find (ii)`P[X<2]`

View SolutionThe probability distribution of X as follows.Find (iii)`P[Xge3]`

View SolutionThe probability distribution of X as follows.Find (ii)`P[X<2]`

View SolutionThe probability distribution of X as follows.Find (ii)`P[X<2]`

View SolutionThree coins are tossed simultaneously.X is the number of heads.Find expected value and variance of X.
View SolutionFind the means and variance of the number randomly selected from 1 to 15.
View SolutionObtain the probability distribution of the number of sixes in two tosses of a fair die.
View SolutionThe pmf of r.v.X as follows.`P(X=0)=3k^3,P(X=1)=4k-10k^2,P(X=2)=5k-1,P(X=x)=0` for any other value of x.(ii)Obtain the cdf F(x).
View SolutionVerify whether each of the following function can be regarded as pmf for the given value of X.(i)
View SolutionVerify whether each of the following function can be regarded as pmf for the given value of X.(ii)P(X)=(x-1)/3,x=1,2,3,P(X)=0,otherwise.
View SolutionGiven below is probability distribution of X. find k

View SolutionGiven below is probability distribution of X.(iii)`P(X<3)`

View SolutionGiven below is probability distribution of X.(iii)`P(X<3)`

View SolutionGiven below is probability distribution of X.(iv)`P(Xle1)`

View Solution
View SolutionComplete the table:
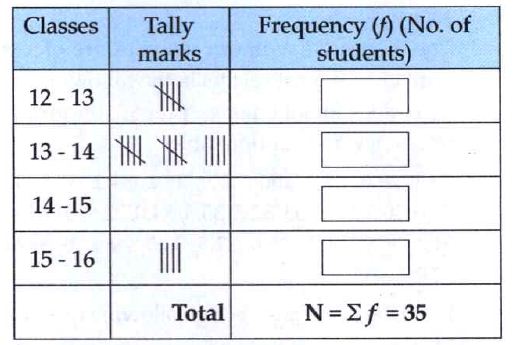
View SolutionThe pmf of r.v.X as follows:`P(x)=C/x^3`x=1,2,3,P(x)=0,otherwise.Find the expected value of X.
View SolutionVerify which of the following is p.d.f of r.v.X : `(i)f(x)=sin x,` for `0lexlepi/2`
View SolutionVerify which of the following id p.d.f of r.v.X:
(i)` f(x)= sinx` for `0lexlepi/2`
(ii)`f(x)= {[x, 0lexle1],[ 2-x , 1ltxlt2]}`
(iii) `f(x)=2` for `0lexle1`
View SolutionVerify which of the following is p.d.f of r.v. X :
(iii) `f(x)=2`, for `0lexle1`
View SolutionIt is known thet error in measured of reaction temperature (in `0^@`) in certain experiment is continous r.v given by `f(x)=x^2/3,for `-1
View SolutionIt is known thet error in measured of reaction temperature (in `0^@`) in certain experiment is continous r.v given by `f(x)=x^2/3,for `-1
View SolutionIt is known that error in measured of reaction temperature (in `0^@`) in certain
experiment is continous r.v given by `f(x)=x^2/3`, for -1 < x < 2 and `=0` otherwise
(iii) Find probability that X is negative
View SolutionSuppose that X is waiting time in minutes for a bus and its p.d.f is given by.`f(x)=1/5,for 0lexle5` and =0 otherwise.Find the probability that (i)Waiting time is between 1 and 3.
View SolutionThe following is the p.d.f of continuous r.v.`f(x)=x/8,for 0ltxlt4` and `x=0` otherwise.
(i)Find expression for c.d.f of X
View SolutionThe following is the p.d.f of continuous r.v.`f(x)=x/8`,for 0
View SolutionGiven that p.d.f of a continuous r.v. `f(x)=x^2/3`, for `-1 < x < 2` and
`=0` otherwise. Determine c.d.f of X hence find
`P(x<1)`, `P(x < -2)`, `P(X>0)`, `P(1 < x < 2)`.
View SolutionIf a r.v. X has p.d.f., `f(x)=c/x`, for `1 < x < 3, c > 0`,
find c, `E(X) and var(X)`
View SolutionSuppose error invloved in making a certain measurements is continuous r.v.X with P.d.f `f(x)=k(4-x^2),for -2lexle2` and =0 otherwise.Compute (i)`P(X>0)`
View SolutionSuppose error invloved in making a certain measurements is continuous r.v. X with p.d.f.
`f(x)=k(4-x^2)`, `for -2lexle2`
and `=0` otherwise.
Compute (ii)`P(-1 < x < 1)`
View SolutionThe p.d.f. of r.v. X is given by
`f(x)=1/(2a)`, for 0 < x < 2a
and `= 0` otherwise.
show that `P(X < frac{a}{2})=P(X > frac{3a}{2})`
View SolutionThe p.d.f of random variable of X is given by
`f(x)=k/sqrt x`,for `0 < x < 4` and
`=0`,otherwise.
Determine K. Determine c.d.f of X and hence `P(Xle2) and P(Xle1)`
View SolutionLet X be a continuous random variable whose probability density function is `f(x)=x^3/4` for `0 < x < c`.
What is the value of the constant c, that makes f(x) a valid
probabilitty density function? What is cdf of X?
View SolutionVerify the following functions are p.d.f of a continuous r.v. X
(i)`f(x)=e^(-x)`, for `0 < x < infty` and `0`, otheriwse
View SolutionFor each of the following p.d.f of r.v.X,find (a)`P(x<1) and (b)P(|X|<1)`(i)`f(x)-x^2/18,for -3
View SolutionFor each of the following p.d.f of r.v.X,find (a)`P(x<1) and (b)P(|X|<1)`(i)`f(x)-x^2/18,for -3
View SolutionFind the c.d.f. `f(x)=3(1-2x^2)` for `0 < x < 1`
and `=0`,otherwise.
Also find `P(1/4 < x < 1/3)` by using pdf and cdf.
View SolutionLet `f(x)=1/x^2,1 < x < infty`
`=0`,otherwise
be the pdf of a r.v. X if `C_1={x:1 < X <2}` and `C_2={x:4 < X < 5}`,
find `P(C_1 uu C_2)`.
View SolutionLet X=amount of time for which on book is taken out of a college library by a randomly selected student and suppose X has pdf `f(x)=0.5x,0lexle2`,and =0,otherwise.Calculate (ii)`P(0.5leXle1.5)`
View SolutionLet X = amount of time for which on book is taken out of a college
library by a randomly selected student and suppose X has pdf
`f(x)=0.5x,0lexle2`, and
`=0`,otherwise.
Calculate (iii) `P(X>1.5)`
View SolutionLet X denote the reaction temperature (in `0^@ C`) of a certain chemical process.Let X be a continuous r.v.with pdf `f(x)=kx^2,-5lexle5=0`,otherwise.Compute `P(X<0)`.
View SolutionLet X =time (in minutes) that elapser betweeb the bell and the end of the lecture in case of a college professor.Suppose X has a pdf.`f(x)=kx^2,0lexle2` and =0,otherwise.(i)Find k.
View SolutionLet X =time (in minutes) that elapser betweeb the bell and the end of the lecture in case of a college professor.Suppose X has a pdf.`f(x)=kx^2,0lexle2` and =0,otherwise.(ii)What is the probability that lecture ends within 1 minute of the bell ringing.
View SolutionLet X =time (in minutes) that elapser betweeb the bell and the end of the lecture in case of a college professor.Suppose X has a pdf.`f(x)=kx^2,0lexle2` and =0,otherwise.(iii)What is the probability that lecture continues for atleast 90 seconds beyond the bell?
View Solution
View Solution
View Solution
View SolutionA r.v.X assumes values 1,2,3….n with the equal probabilities.
(ii) What will be n if `var(x)=E(x)`.
View SolutionThe pdf of r.v.X is given by `f(x)=k/sqrt(x) ,0 < x< 4`.
`=0`,otherwise.
Determine k. Determine c.d.f. of x and hence find `P(xle2),P(2 < X < 3), P(Xge1)`.
View SolutionDetermine K if `f(x)=Ke^(- theta x),0lex < theta,theta > 0`
`=0`,otherwise
is the p.d.f. of r.v. X. Also find `P(X > 1/theta)` and find M if `P(0 < X < m)=1/2`.
View Solution
View SolutionA r.v.X has the following probability distribution.(ii)Find `P(0 < x < 4)`
View SolutionGiven that p.d.f of a continuous r.v.
`f(x)=x^(2/3)`, for `1 < x < 2`
and `=0` otherwise.
Determine c. d. f. of X hence find `P(x < 1),P(x > 2),P(X > 0),P(1 < x < 2)`.
View SolutionFind K,such that the function `P(x)=K(4,3),x=0,1,2,3,4,K>0`=0,otherwise is a pmf.
View SolutionFind the expected value,variance and standard deviation of a random variable X whose pmf is given below.

View SolutionThe pmf for X=numbers of major defects in a randomly selected appliance of a certain type is .Find the expected value and variance of X.

View SolutionThe time (in minutes)that a lab assistant to prepare the equipment for a certain experiment is a random variable taking values between 25 and 35 minutes with pdf `f(x)=1/10,25lexle35`,=0,otherwise.What is the probability that preparation time exceed 33 minutes?Also find cdf of X.
View SolutionP.d.f of a c.r.v X is `f(x)=6x(1-x)`,for `0lexle1`
and =0,otherwise(elsewhere) If `P(X < a)=P(X > a)`, then a=
View SolutionIf the p.d.f of a r.v.x is `f(x)=3(1-2x^2),``for`` 0ltxlt1 and =0`,other wise(elsewhere)then the c.d.f of X is F(x)=
View SolutionIf the p.d.f of a c.r.v. X is `f(x)=x^2/18`, for `-3 < x < 3`
and `=0`, other wise then `P(|X| < 1)`=
View SolutionIf p.m.f of a d.r.v.X is `P(X=x)=(^5C_X)/2^5`, for `x=0,1,2,3,4,5`
and `=0`,otherwise
If `a=P(Xle2)` and `b=P(Xge3)`,then `E(X)=`
View SolutionIf X denotes the number obtained on the uppermost face
when a fair die is thrown,then `Var(X)` is
View SolutionIf X is a r.v with pmf `P(x)=kx,for x=1,2,3`,=0,otherwise,then K=………..
View SolutionLet pmf of a random variable X is `P(x)=(3-x)/10`,x=-1,0,1,2.=0,otherwise.Then E(x) is…
View SolutionIf the pdf of continuous random variable X is given as `f(x)=x^2/3,-1 < x < 2`
`=0`,otherwise.
Then c.d.f.X is…….
View SolutionIf the p.d.f of a c.r.v. X is `f(x)=x^2/18`, for `-3 < x < 3`
and `=0`, other wise then `P(|X| < 1)`=
View SolutionVerify whether `f(x)=sin x` for `0lexlepi/2` is pdf of r.v.X.
View Solution
EXERCISE questions and complete solutions for chapter PROBABILITY DISTRIBUTIONS of CHETANA PUBLICATION of Class 12