Complete Solutions to Example of chapter Magnetic Fields due to Electric Current of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | Magnetic Fields due to Electric Current |
| CHETANA PUBLICATION | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Explain the conclusion led by Oersted experiment.
01:46View SolutionState the expression for the magnetic force acting on a electron moving with velocity `barv` in a magnetic field `barB` .
02:22View SolutionState the formula for Lorentz force acting on a charge in presence of electric as well as magnetic field.
02:38View SolutionState the expression for magnetic force acting on a charge moving with velocity `barv` in an uniform magnetic field `barB` . State the important features of this force?
01:46View SolutionState the SI unit as well as non SI unit of magnetic field Define its SI units. Find its dimension.
03:16View SolutionIf the magnetic field is parallel to the positive y axis and the charged particle is moving along the positive x axis, then what would be the direction of Lorentz force be for:- an electron
01:42View SolutionIf the magnetic field is parallel to the positive y axis and the charged particle is moving along the positive x axis, then what would be the direction of Lorentz force be for:- a proton.
03:05View SolutionA charged particle moves with a velocity `3 xx 10^6 m//s` at right angles to a uniform magnetic field of induction 0.005T. Find the magnitude of the charge if the particle experience a force of `2 xx 10^-2N`.
03:15View SolutionA charged particle travels with a velocity `barv` through uniform magnetic field B as shown in the following figures. What is the direction of the magnetic force `f_m` due to magnetic field on the particle?
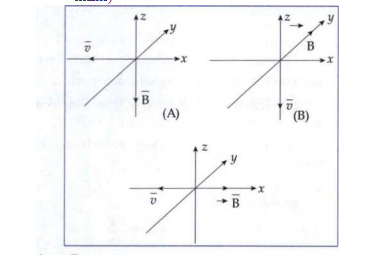 03:46View Solution
03:46View SolutionExplain why a charged particle in a particle accelerator the cyclotron describes circular motion. Derive cyclotron formula.
09:46View SolutionWhat is cyclotron?
03:00View SolutionExplain the function of electric field and magnetic field in a cyclotron?
04:50View SolutionWhat are the factors on which the cyclotron frequency depends?
02:41View SolutionWhat are the factors on which the maximum kinetic energy acquired by the particle in the cyclotron depends?
02:55View SolutionDoes the time spent by a charged particle inside a dee of a cyclotron depends upon its speed and the radius of its path? Why?
03:03View SolutionExplain the construction and working of cyclotron.
03:45View SolutionState the uses of cyclotron of particle accelerators
03:53View SolutionExplain the working of the cyclotron and find the expression for the time period of revolution of the charged particle.
05:21View SolutionShow that cyclotron frequency for charged particle is `(qB)/(2pim)`. What is resonance condition?
05:25View SolutionObtain an expression for K.E. of a positively charged particle.
03:47View SolutionState the limitations of cyclotron.
05:41View SolutionFor proton acceleration, a cyclotron is used in which a magnetic field of `1.4 Wb//m2` is applied find the time period for reversing the electric field between the two Ds. Given that mass of the proton = `1.67 x 10^-27 kg`, charged proton = `1.6 xx 10^-19 C`
03:05View SolutionAn electron is moving with a speed of `3 xx 10^7m//s` in a magnetic field of `6 xx 10^-4 T` perpendicular to its path. What will be the radius of the path? What will be the frequency and the energy in keV? Given: mass of electron = `9 xx 10^-31 kg`, charge e = `1.6 xx 10^-19C`, lev = `1.6 xx 10^-19 J`.
06:26View SolutionAn alpha particle (the nudeus of a helium atom) (with charge +2) is accelerated and moves in a vacuum tube with kinetic energy 10 MeV. It passes through a uniform magnetic field of 1.88T, and traces a circular path of radius 24.6cm. Obtain the mass of the alpha particle. [leV = `1.6 xx 10^-19 J`, charge of electron = `1.6 xx 10^-19C`]
05:10View SolutionIn a cyclotron protons are to be accelerated. Radius of the D is 60 cm and its oscillator frequency is 10 Mhz. What will be the kinetic energy of the accelerated proton? Proton mass = `1.67 xx 10^-27 kg`, e = `1.6 xx 10^-19C` lev = `1.6 xx 10^-19 J`
01:40View SolutionExplain the helical motion of a charged particle is a magnetic field `barB`.
08:52View SolutionDerive an expression for force experienced by a current carrying straight wire in a uniform magnetic field B. Discuss when will it be maximum and minimum.
05:45View SolutionExplain how will the magnetic force acting on a arbitrary shaped wire be expressed.
04:02View SolutionWhat will be the force on a closed circuit on a magnetic field B ?
03:55View SolutionConsider a square loop of wire loaded with a glass bulb of mass m hanging vertically, suspended in air with its one part in a uniform magnetic field B with its direction coming out of the plane of paper. Due to the current I flowing through the loop, there is a magnetic force in upward direction calculate the current I in the loop for which the magnetic force would be exactly balanced by the force on mass m due to gravity.
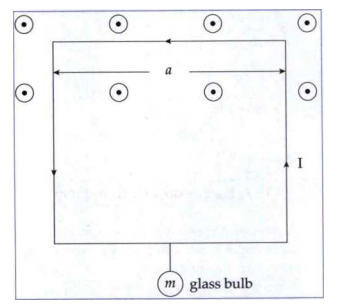 03:25View Solution
03:25View SolutionA piece of straight wire has mass 20g and length lm. It is to be levitated using a current of 1A flowing through. A perpendicular magnetic field B in a horizontal direction is applied what must be the magnetic field B? take `g = 9.8 m//s^2`
 03:59View Solution
03:59View SolutionDerive an expression for torque acting on a rectangular current loop carrying coil placed in a uniform magnetic field.
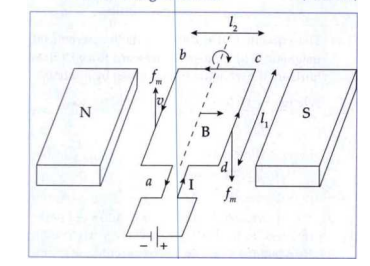 08:43View Solution
08:43View SolutionA rectangular coil of 100 turns of length 40 cm and breadth 20 cm carrying a current of 10 A is placed making a angle of `60^@` with a magnetic field of 5T:- Calculate the magnitude of the counter torque, that must be applied to prevent the coil from turning.
04:02View SolutionA rectangular coil of 100 turns of length 40 cm and breadth 20 cm carrying a current of 10 A is placed making a angle of `60^@` with a magnetic field of 5T:- Would the answer change of the rectangular coil is replaced by a planar coil of some irregular shape that encloses the same area? All other particular are also unaltered.
03:30View SolutionWith the help of neat labelled diagram, describe construction, theory and working of a moving coil galvanometer.
09:22View SolutionExplain the construction and working of a moving coil galvanometer. Hence, show that a current flowing through it is directly proportional to the deflection.
10:13View SolutionA moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions `5 cmi xx 3 cm`. The radial magnetic field in which the coil is suspended is of `0.05 wb//m^2`. The torsional constant of the spring is `1.5 xx 10^-9 Nm//degree`. Obtain the current required to be passed through the galvanometer so as to produce a deflation of `30^@`.
04:09View SolutionA rectangular coil of effective area `0.05 m^2` is suspended freely in a radial field of `0.01 Wb//m^2`.If the torsional constant of suspension fibre is `5 xx 10^-9 N//m` per degree, find the angle through which the coil rotates when a current of `300 muA` is passed through it.
03:52View SolutionDefine magnetic dipole moment of a current carrying coil.
01:59View SolutionA circular coil of conducting wire has 500 turns and an area `1.26 xx 10^-4 m^2` is enclosed by the coil. Calculate the magnetic moment of the coil if a current of `100 muA` is passed through.
01:42View SolutionDerive an expression for magnetic potential energy for a magnetic dipole freely suspended in a uniform magnetic field B.
03:25View SolutionState when magnetic potential energy is maximum and minimum, also state which is the most `stable//unstable` position.
03:51View SolutionState and explain Biot-Savart's Law.
05:47View SolutionState Biot-Savart's Law and write it in vector form.
02:43View SolutionState the expression for magnetic field due to:- infinity long, straight wire,
04:51View SolutionState the expression for magnetic field due to:- semi - infinite straight wire.
03:17View SolutionDerive an expression for the magnetic field due to an infinitely long straight wire carrying current I.
13:44View SolutionCalculate the value of magnetic field at a distance of 2 cm from a very long straight wire carrying a current of 5A. Given `mu_0 = 4pi xx 10^-7 Wb//Am`
02:02View SolutionA very long straight wire carries a current 5.2A. What is the magnitude of the magnetic field at a distance 3.1 cm from the wire?
02:44View SolutionMagnetic field at a distance 2.4 cm from a long straight wire is `16muT`. What must be current through the wire?
03:48View SolutionTwo long parallel wires going into the plane of the paper are separated by a distance R and carry a current I each in the same direction. Show that the magnitude of the magnetic field at a point P equidistance from the wires and subtending angle `theta` from the plane containing the wires is `B=(mu_0)/pi I/R sin2theta` What is the direction of the magnetic field?
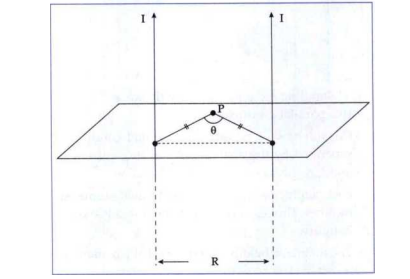 07:46View Solution
07:46View SolutionDerive an expression for the force acting per unit length of the wire in case of two long parallel wires carrying currents.
05:12View SolutionState the expression for force acting per unit length of each of the straight wire conducting current. Hence define SI unit of electric current.
04:21View SolutionCurrent of equal magnitude flows through two long parallel wires having separation of 1.35 cm. If the force per unit length on each of the wires is `4.76 xx 10^-2 N//m`,What must be the value of current?
03:47View SolutionTwo wires shown in the figure are connected in a series circuit and the same amount of current of 10A passes through both, but in opposite directions seperation between the two wires is 8 mm. The length AB is S = 22 cm. Obtain the direction and magnetic field due to current in wire 2 on the section AB of wire 1. Also obtain the magnetic and direction of the force on wire 1.`(mu_0=4pixx10^-7TmA^-1)`.
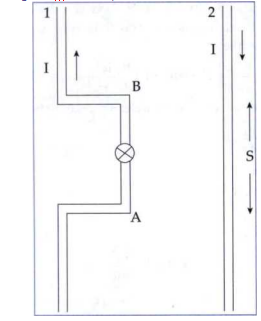 06:28View Solution
06:28View SolutionDerive an expression for the magnetic field produced by a current flowing through a circular arc of the wire.
05:24View SolutionFind the value of magnetic field produced by a current flowing through a semi circular arc of wire.
02:24View SolutionState the expression for the magnetic field at the centre of a full circle of a wire carrying a current I.
05:24View SolutionDerive an expression for the magnetic field produced by a current flowing through a circular arc of the wire.
05:24View SolutionState the expression for the magnetic field due to a circular are of wire carrying a current I. Hence find the magnetic field at the centre of circular coil and having n turns.
03:40View SolutionA wire has 2 straight and one are as shown in the figure. Determine the direction and magnitude of the field produced at the center O of the semi circle by three sections individually and the total.
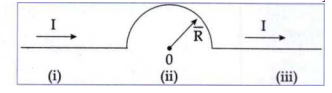 02:51View Solution
02:51View SolutionThe magnetic field at the centre of a circular current carrying loop of radius 12.3 cm is `6.4 xx 10^-6T`. What will be the magnetic moment of the loop? `(mu_0 = 4pi xx 10^-7 TmA^-1)`
04:31View SolutionA circular coil of wire is made `phi` of 100 turns, each of radius 8 cm if a current of 0.4A passes through of, what will be the magnetic field at the centre of the coil
03:01View SolutionA semicircular arc of radius 20 cm carries a current of 10 A calculates the magnitude of magnetic field at the centre of the arc.
03:23View SolutionTwo circular coils have radii in ratio `3:4` and ratio of number of turns is `2:3`. The ratio of currents through coils is `1:4` find the ratio of magnetic induction of their centre.
03:03View SolutionThe electron in a hydrogen atom circles around the positive nucleus with a speed of `2.18 xx 10^6 m//s` in an orbit of radius `5.3 x 10^-11 m`. Calculate the:- equivalent current
03:01View SolutionThe electron in a hydrogen atom circles around the positive nucleus with a speed of `2.18 xx 10^6 m//s` in an orbit of radius `5.3 x 10^-11 m`. Calculate the:- Magnetic field produced at the proton. Given e = `1.6 xx 10^-19 c`, `mu_0 = 471 xx 10^-7 Wb//Am`
04:24View SolutionTwo identical coils each of radius r and having number of turns n are lying in perpendicular planes such that they have common centre. Find the magnetic field at the centre of the coils if they carry currents equal to I and `sqrt31` respectively.
03:38View SolutionA wire loop is formed by joining two semicircular wires of radii `r_1` and `r_2` as shown in the figure if the loop carries a current `I_1` find the magnetic field at the centre O.
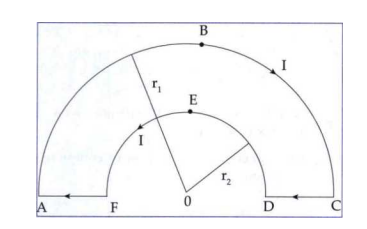 .04:50View Solution
.04:50View SolutionAn electric current I is flowing through an infinitely long conductor bent into the from as shown in the figure. Find the magnitude and direction of magnetic field at the centre of the semi-circular part of the conductor.
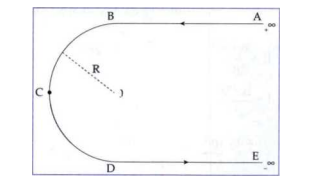 04:37View Solution
04:37View SolutionA wire loop of the form shown the figure carries a current. Obtain the magnitude and direction of the magnetic field at P.
 03:38View Solution
03:38View SolutionFind an expression for the axial magnetic field produced by current in a circular lopp?
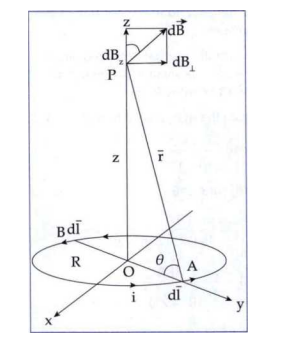 .06:18View Solution
.06:18View SolutionA circular loop of radius 9.7 cm carries a current 2.3A. Obtain the magnitude of the magnetic field:- centre of the loop .
02:16View SolutionA circular loop of radius 9.7 cm carries a current 2.4A. Obtain the magnitude of the magnetic field:- at a distance of 9.7cm from the centre of the loop but on the axis. .
03:18View SolutionCalculate the magnitude of the magnetic induction due to a circular coil of 400 turns and radius 0.05 cm, carrying a current of 5A, at a point on the axis of the coil at a distance of 0.1 m from the centre of the coil.
02:51View SolutionExplain how a current loop acts as a magnetic dipole.
04:15View SolutionState right hand thumbrole for a circular coil.
03:10View SolutionState the expression for magnetic field at an axial point produced by current carrying loop. Hence find the expression for the magnetic field:- at the centre of a loop,
05:26View SolutionState the expression for magnetic field at an axial point produced by current carrying loop. Hence find the expression for the magnetic field:- at the centre of a coil having N turns.
02:28View SolutionFrom the expression of magnetic field at an axial point due to current carrying loop, find the expression for magnetic field at a large distance from the loop along z axis. Is it analogous to electric field due to an elextric dipole?
05:42View SolutionWhat is the fundamental difference between an electric dipole and magnetic dipole?
03:24View SolutionDefine magnetic dipole moment for a current carrying circular loop.
02:48View SolutionConsider a closely wound 1000 turn coil having a radius of lm. If a current of 10A basses through the coil, what will be the magnitude of the magnetic field at the centre?
01:52View SolutionA current of 10A passes through a coil having 5 turns and produces a magnetic field of magnitude. `5 xx 10^-4T` at th e centre of the coil. Calculate the diameter of the coil.
02:47View SolutionUsing electrostatic analogue, obtain the magnetic field at a distance 'x' on the perpendicular bisector of a magnetic dipole `mu` for x » R, verify that `barB=(mu_0)/(4pi)(pi)/(x^2)`
03:26View SolutionState Ampere's Law.
02:44View SolutionState and explain Ampere's law.
05:03View SolutionExplain how the expression for magnetic field due to, straight conductor derived from Biot Savart's law is in accordance with Ampere's circuital law.
03:02View SolutionA very long straight wire carries a current of 5A. The magnetic induction at 0.1m from the wire is `1 xx 10^-5 wb//m^2`. What will be the magnetic induction at 0.5m from the wire of the current through the wire is increased to 20A?
03:03View SolutionA coaxial cable consists of a central conducting core wire of radius, a and a coaxial cylinderical outer conductor of radius h (see figure). The two conductor carry an equal current I in opposite directions in and out of the plane of the paper what will be the magnitude of the magnetic field B for:- b < r?what will be its direction?
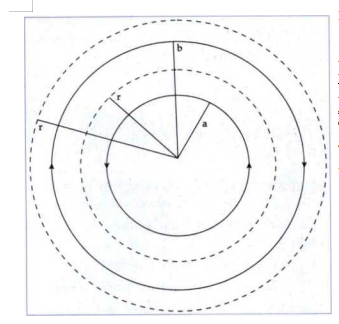 03:32View Solution
03:32View SolutionA coaxial cable consists of a central conducting core wire of radius, a and a coaxial cylinderical outer conductor of radius h (see figure). The two conductor carry an equal current I in opposite directions in and out of the plane of the paper what will be the magnitude of the magnetic field B for:- b < r?what will be its direction?
 03:32View Solution
03:32View SolutionFigure shows a cylinderical wire diameter a, carrying a current I. The current density which is in the direction of the central axis of the wire varies linearly with radias distance V from the axis according to the relation `J = J_0r//a`. Obtain the magnetic field B inside the wire at a distance r' from its centre.
 04:39View Solution
04:39View SolutionIn the above problem, what will be the magnetic field B inside the wire at a distance r from its centre. If the current density J is uniform across the cross section of the wire.
06:54View SolutionWhat is a solenoid? Explain with a diagram Refer to the magnetic field produced by a current carrying solenoid.
03:06View SolutionFind the expression for the magnetic field produced by a current carrying solenoid.
06:09View SolutionWhat is a toroid? With neat labelled diagram, describe the magnetic field produced by current carrying toroid.
07:01View SolutionA solenoid of length `pi m` and 5 cm in diameter bas winding of 1000 turns and carries a current of 5A. Calculate the magnetic field at tits centre along the axis
02:12View SolutionA solenoid 0.5 m long has a four layer winding of 300 turns each. What current must pass through it to produce a magnetic field of induction `2.1 xx 10^-2 T` at its centre?
03:10View SolutionA solenoid 1 m long and 4 cm diameter possesses `10 tums//cm`. A current of 5A is flowing through it. Calculate the magnetic induction:- inside the solenoid
02:36View SolutionA solenoid 1 m long and 4 cm diameter possesses `10 tums//cm`. A current of 5A is flowing through it. Calculate the magnetic induction:- at one end on the axis of solenoid.
03:17View Solution
Example questions and complete solutions for chapter Magnetic Fields due to Electric Current of CHETANA PUBLICATION of Class 12
