Complete Solutions to EXERCISE 3 (Long Answer Type Questions) of chapter BINARY OPERATION of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | BINARY OPERATION |
| CHHAYA PRAKASHINI | EXERCISE 3 (Long Answer Type Questions) |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
A binary operation `@` is defined on `RR-{-1}` by `a@b=a+b+ab` for all `a,binRR-{-1}.`
(i) Discuss the commutativity and associativity of `@` on `RR-{-1}`.
Find the identity element, if exists.
(iii) Prove that every element of `RR-{-1}` is invertible.06:06View SolutionThe binary operation multiplication modulo `10(xx_(10))` is defined on the set ` A={0,1,3,7,9,},` find the inverse of the element 7.
03:49View SolutionConstruct the composition table for the binary operation multiplication modulo `5(xx_(5))` on the set `A={0,1,2,3,4}`.
03:04View SolutionA binary operation `**` on `NN` is defined by `a**b=L.C.M.(a,b)` for all `a,binNN`.
(i) Find `15**18`
(ii) Show that `**` is commutative as well as associative on `NN.`
(iii) Find the the identity element in `NN`.
(iv) Also find the invertible element in `NN`.07:40View SolutionLet P(A) b the power set of non-empty set A. A binary operation `**` is defined on P(A) as `X**Y=XcapY` for all `X,YinP(A)`. Detemine the identity element In P(A). Prove that A is the only invertible element in P(A).
04:31View SolutionA binary operation `**` is defined in `QQ_(0)`, the set of all non-zero rational numbers, by `a**b=(ab)/(3)` for all `a,binQQ_(0)`. Find the identity element in `QQ_(0)`. Also find the inverse of an element `x in QQ_(0)`.
02:47View SolutionLet `P(C )` be the power set of non-empty set C. A binary operation `**` is defined on P(C ) as `A**B=(A-B)cup(B-A)` for all `A,BinP(C )`. Prove that `Phi` is the identity element for `**` on P(C ) and A is invertible for all `AinQQ_(0)`.
04:22View SolutionLet `A=Ncup{0}xxNNcup{0},` a binary operation `**` is defined on A by. `(a,b)**(c,d)=(a+c,b+d)` for all `(a,b),(c,d)inA.` Prove that `**` is commutative as well as associative on A. Show also that (0,0) is the identity element In A.
06:21View SolutionLet `A={0,1,2,3,4,5}` be a given set, a binary operation `@` is defined on A by `a@b=ab(mod6)` for all `a,bin A.` Find the identity element for `@` in A . Show that 1 and 5 are the only invetible elements in A.
04:10View SolutionLet `A=NNxxNN`, a binary operation `**` is defined on A by `(a,b)**(c,d)=(ad+bc,bd)` for all `(a,b),(c,d)inA.` Show that `**` possesses no identity element in A.
03:18View SolutionFind the values of
(i) `4+_(6)2` (ii) `7+_(5)7` (iii) `5+_(8)2`
(iv) `3xx_(7)2` (v) `12xx_(10)5` (vi) `6xx_(5)4`05:16View SolutionLet `M_(2)(x)d={:{((x,x),(x,x)):},x inRR}` be the set of `2xx2` singular matrices. Considering multiplication of matrices as a binary operation, find the identity element in `M_(2)(x)`. Also find the inverse of an element of `M_(2)`.
05:50View SolutionPrepare the composition table for addition modulo `6 (+_(6))` on `A={0,1,2,3,4,5}`.
03:36View SolutionPrepare the composition table for multiplication modulo 6 `(xx_(6))` on `A={0,1,2,3,4,5}.`
03:04View SolutionA binary operaiton `^^` on the set `A={1,2,3,4,5}` is defined by `a^^b=min(a,b)` for all `a,binA.` prepare composition table for the operation `^^` on A.
01:52View SolutionLet `S={1,omega,omega^(2)}` be the set of cube roots of unity. Prepare the composition table for multiplication `(xx)` on S, show that multiplication on S is a binary operation and it is commutative on S. Also, show that every element on S is invertible.
04:49View SolutionPrepare the composition table for multiplication `(xx)` on the set of fourth roots of unity and discuss its important properties.
04:25View SolutionComplete the following nultiplication table so as to define a commutative binary operation `**` on `A={1,2,3,4}.`
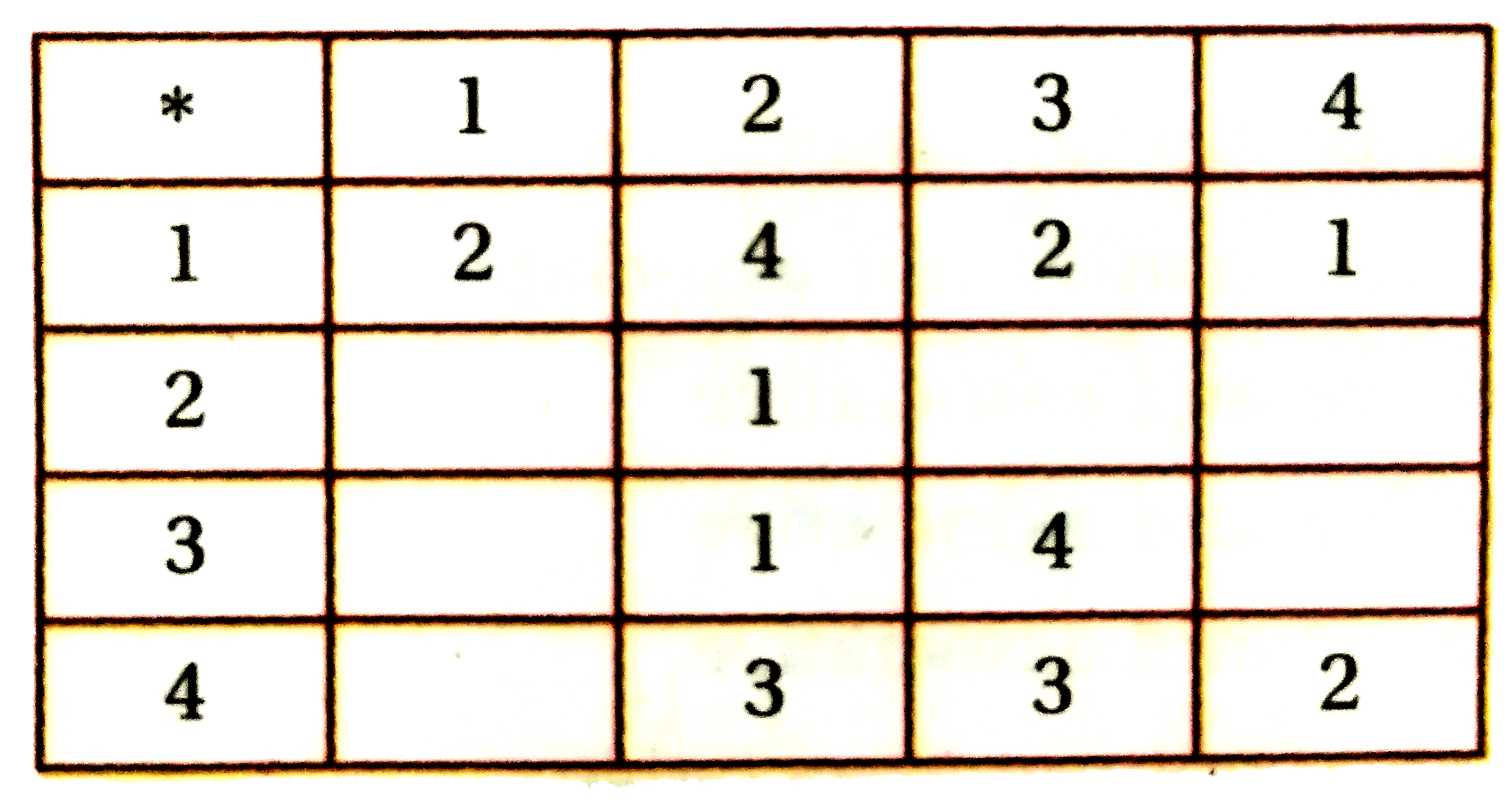 02:43View Solution
02:43View SolutionA binary operation `@` is defined on the set `A={0,1,2,3,4,5}` as follows: `a@b=a+b(mod6)` for all `a,binA.` Prove that `oinA` is the identity element In A is invertible with operation `@` and each element A is invertible with `6-ainA` being the inverse of the element a.
04:21View SolutionAn operation `**` is defined on the set `A={1,2,3,4}` as follows: `a**b,ab(mod5)` for all `a,binA`.Prepare the compositon table for `**` on A and from the table show that -
(i) multiplication `mod(5)` is a binary operation,
(ii) `**` is commutative on A,
(iii) is the identity element for multiplication `mod(5)` on A, and.
(iv) every element of A is invertible.07:41View SolutionLet `A={1,-1}` be the set of square roots of unity. Considering multiplication `(xx)` as a binary operation on A, construct the composition table for multiplication on A. Determine the identity element for multiplication in A and the inverses of the elements.
01:39View SolutionLet `**` be the binary defined on the set `S={1,2,3,4,5,6}` by `a**b=r` where r is the least non-negative remainder when ab is divided by 7. Prepare the composition table `**` on S. Observing the composition table show that 1 is the identity element for `**` and every element of S is invertible.
05:18View Solution
EXERCISE 3 (Long Answer Type Questions) questions and complete solutions for chapter BINARY OPERATION of CHHAYA PUBLICATION MATHS (BENGALI ENGLISH) of Class 12
