Complete Solutions to All Questions of chapter HEAT AND THERMODYNAMICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | HEAT AND THERMODYNAMICS |
| D MUKHERJEE | All Questions |
| Number Of Questions | 85 |
| Academic Year | 2023-24 |
Two holes of unequal diameters `d_(1)` and `d_(2)(d_(1)gt d_(2))` are cut in metal sheet is heated
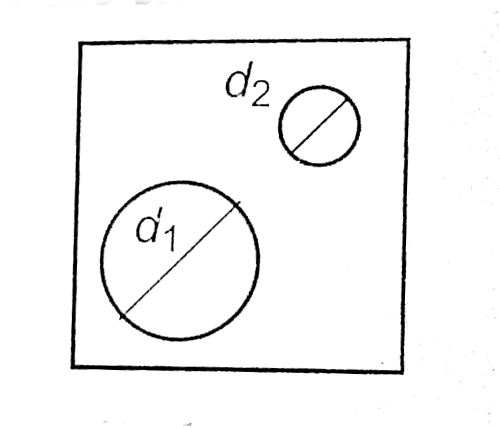
View SolutionIn the previous question, the distance between the hole will
View SolutionA metal wire of length jl and area of cross - section A is fixed between rigid supports negligible tension . If this is cooled. The tension in the wire will be
View SolutionTwo metal rods of the same length and area of cross-section are fixed end to end between rigid supports. The materials of the rods have Young module `Y_(1)` and `Y_(2)` , and coefficient of linear expansion `alpha_(1)` and `alpha_(2)` . The junction between the rod does not shift and the rods are cooled
View SolutionThree rods of equal of length are joined to from an equilateral triangle ABC. `D` is the midpoint of AB. The coefficient of linear expansion is `alpha_(1)` for AB and `alpha_(2)` for `AC` and `BC` . If the distance `DC` remains constant for small changes in temperature,

View Solutionwhen the temperature of a body increses from t to `t +Deltat`,its moment of inertia increases form I to ` I + DeltaI`. The coefficient of linear expanison of the body is `prop`. The ratio`(DeltaI)/I` is equal to
View SolutionA horizontal tube, open at both ends, contains a column of liquid. The length of this liquid column does not change with temperature. Let `gamma` : coefficient of volume expansion of the liquid and `alpha` : coefficient of linear expansion of the material of the tube
View SolutionIn a vertical `U`-tube containing a luquid, the two arms are maintained at different temperatures, `t_(1)` and `t_(2)` . The liquid coplumns in the two arms have heights `l_(1)` and `l_(2)` respectively. The coefficient of volume expansion of the liquid is equal to

View SolutionA solid whose volume does not change with temperature floats in a liquid. For two different temperatures `t_1` and `t_2` of the liqiud, fraction `f_1` and `f_2` of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to
View SolutionA solid with coefficient of linear expansion `aplha` just floats in a liquid whose coefficient of volume expansion is `gamma` . If the system is heated, the solid will
View SolutionA gas at 300 K has pressure `4 xx 10^(-10) N//m^(2)`. IF `k = 1.38 xx 10^(-23) J//K`, the number of `"molecule"// cm^(3)` is of the order of
View SolutionThe root mean square (r.m.s) speed of oxygen molecules `(O_2)`
at a certain temperature T (degree absolute) is V. If the temperature is doubled and oxygen gas dissociates into atomic oxygen, the r.m.s speed remains unchanged.
View SolutionThe average translational kinetic energy of `O_(2)` (molar mass 32) molecules at a particular temperature is `0.048 eV`. The translational kinetic energy of `N_(2)` (molar mass 28) molecules in (eV) at the same temperature is (JEE 1997)
(a) 0.0015 (b) 0.003 ( c) 0.048 (d) 0.768
View SolutionA gas has volume `V` and pressure `p`. The total translational kinetic energy of all the molecules of the gas is
View SolutionA closed vessel is maintained at a constant temperture. It is first evacuated and then vapour is injected it continuously. The pressure of the vapour in the vessel
View Solutionwhen an air bubble rises from the bottom to the surface of a lake, its radius becomes double . Find the depth of the lake , given that the atmospheric pressure is equal to the pressure due to a column of water 10 m high. Assume constant temperature and disreged surface tension .
View SolutionTwo containers of equal volume contain the same gas at pressure `P_(1)` and `P_(2)` and absolute temperature `T_(1)` and `T_(2)`, respectively. On joining the vessels, the gas reaches a common pressure `P` and common temperature `T`. The ratio `P//T` is equal to
View SolutionTwo idential container joined by a small pipe initially contain the same gas at pressure `p_(0)` and absolute temperature `T_(0)`. One container is now maintained at the same temperature while the other is heated to `2T_(0)`. The common pressure of the gas
View SolutionIn the previous question let `V_(0)` be the volume of each container. All other details remain the same. The number of moles of gas in the container at temperature `2 T_(0)` will be
View SolutionA horizontal cylinder has two sections of unequal cross - sections, in which two pistons can move freely. The pistons are joined by a string, Some gas is trapped between the pistons. If this gas is heated the pistons will

View SolutionA gas expands from 1 litre to 3 litres at atmospheric pressure. The work done by the gas is about
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio `C_P//C_V` for the gas is
View SolutionIn the previous question, the gas may be
View SolutionEach molecule of a gas has F degrees of freedom . The ratio `(C_(p))/(C_(V))=gamma` for the gas is
View SolutionA mixture of `n_(1)` moles of monoatomic gas and `n_(2)` moles of diatomic gas has `(C_(p))/(C_(V))=gamma=1.5`
View SolutionThe pressure `p` for a gas is plotted against its absolute temperature `T` for two different volumes `V_(1)` and `V_(2)`. If `p` is plotted on `y-` axis and `T` on `x-`axis, then
View Solution
A cyclic process ABCD is shown in the p-V diagram. Which of the following curves represent the same process?
View SolutionThe ratio `(C_p)/(C_v)=gamma` for a gas. Its molecular weight is M. Its specific heat capacity at constant pressure is
View SolutionWhen an ideal gas undergoes an adiabatic change causing a temperature change `DeltaT`
(i) there is no heat ganied or lost by the gas
(ii) the work done by the gas is equal to change in internal eenrgy
(iii) the change in internal energy per mole of the gas is `C_(V)DeltaT`, where `C_(V)` is the molar heat capacity at constant volume.
View SolutionWhen an ideal diatomic gas is heated at constant pressure, the fraction of the heat energy supplied, which increases the internal energy of the gas, is
View SolutionThe average degrees of freedom per molecule for a gas are 6. The gas performs `25 J` of work when it expands at constant pressure. The heat absorbed by gas is
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View SolutionA system is taken from state A to state B along two different paths 1 and 2 . The heat absorbed and work done by the system along these two paths are `Q_(1)` and `W_(1)` and `W_(2)` respectively.
View SolutionEqual masses of three liquids A, B and C have temperature `10^(@)C, 25^(@)C` and `40^(@)c` respectively. If A and B are mixed, the mixture has a temperature of `15^(@)C`. If B and C are mixed, the mixture has a temperature of `30^(@)C`, if A and C are mixed will have a temperature of
View SolutionIf water at `0^@C` kept in a container with an open top, is placed a large evacuated chamber,
View SolutionIn the previous question, if the specific latent heat of vaporization of water at `0^@C` is `eta` times the specific latent heat of freezing of water at `0^@C`, the fraction of water that will ultimately freeze is
View SolutionA substance of mass M kg requires a power input of P wants to remain in the molten state at its melting point. When the power source is turned off, the sample completely solidifies in time t seconds. The latent heat of fusion of the substance is …….
View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are `K_(1)` and `K_(2)`. The temperature of the free ends of the first and seconds rods are maintained at `theta_(1)` and `theta_(2)` respectively. The temperature of the common junction is
View SolutionA cylinder of radius `R` made of a material of thermal conductivity `K_(1)` is surrounded by cylindrical shell of inner radius `R` and outer radius `2R` made of a material of thermal con-ductivity `K_(2)` The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View SolutionA spherical black body with a radius of 12 cm radiates 450 watt power at 500 K. If the radius were halved and the temperature doubled, the power radiated in watt would be
View SolutionTwo spherical black bodies of radii `R_(1)` and `R_(2)` and with surface temperature `T_(1)` and `T_(2)` respectively radiate the same power. `R_(1)//R_(2)` must be equal to
View SolutionA body cools from `50^(@)C` to `40^(@)C` in 5 min. The surroundings temperature is `20^(@)C`. In what further times (in minutes) will it cool to `30^(@)C` ?
View SolutionIn the previous question will be its temperature 5 min after reaching `40^(@)C`?
View SolutionA metal rod is shaped into a ring with a small gap. If this is heated,
(i) the length of the rod will increase
(ii) the gap will decrease
(iii) the gap will increase
(iv) the diameter gof the ring will increase in the same ratio as the length of the rod
View SolutionThe average translational energy and the rms speed of molecules in a sample of oxygen gas at `300K` are `6.21xx10^(-21)J` and `484m//s`, respectively. The corresponding values at `600K` are nearly (assuming ideal gas behaviour)
View SolutionLet `barv,v_(rms) and v_p` respectively denote the mean speed. Root mean square speed, and most probable speed of the molecules in an ideal monoatomic gas at absolute temperature T. The mass of a molecule is m. Then
View SolutionTwo identical containers A and B have frictionaless pistons. They contain the same volume of an ideal gas at the same temperature. The mass of the gs in A is `m_(A)` and that B is `m_(B)` . The gas in each cylinder is now allowed to expand isothermally to double the intial volume. The chages in the pressure in A and B are fopund to be `Delta` and `1.5Deltap` respectively.
View SolutionA gas undergoes a process in which its pressure `P` and volume `V` are related as `VP^(n) =` constant. The bulk modulus of the gas in the process is:
View SolutionA gas with `(c_(p))/(c_(V))=gamma` goes from an intial state `(p_(1), V_(1), T_(1))` to a final state `(p_(2), V_(2), T_(2))` through an adiabatic process. The work done by the gas is
View SolutionA gas may expand either adiabatically or isothermally. A number of `p-V` curves are drawn for the two processes over different ranges of pressure and volume, it will be found that
(i) Two adiabatic curves do not intersect
(ii) two isothermal curves do not intersect
(iii) an adiabatic curve and an isothermal curve may intersect.
(iv) the magnitude of the slope of an adiabatic curve is greater than the magnitude of the slope of an isothermal curve
View SolutionA gas expands such that its initial and final temperatures are equal. Also the process followed by the gas traces a straight line on the `P-V` diagram
(i) The temperature of the gas remains constant throughout
(ii) The temperature of the gas first increases and then decreases
(iii) The temperature of the gas first decreases and then increases
(iv) The straight line has negative slope
View Solution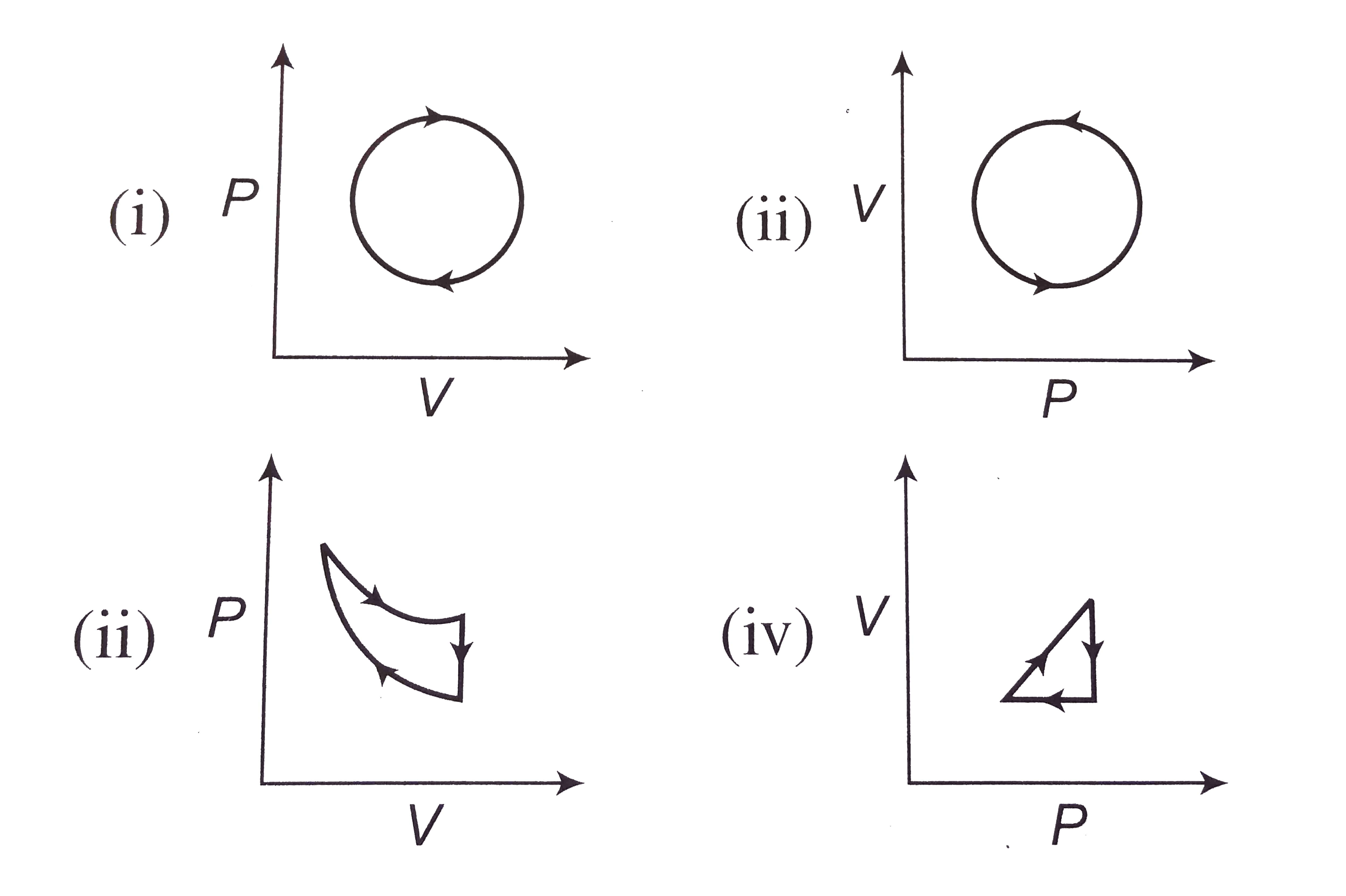
The following are the `P-V` diagrams for cyclic processes for a gas. In which of these processes is heat absorbed by the gas?
View SolutionTwo gases have the same initial pressure, volume and temperature. They expand to the same final volume, one adiabatically and the other isothermally
View SolutionIn the previous question, if the two gases are compressed to the same final volume,
View Solution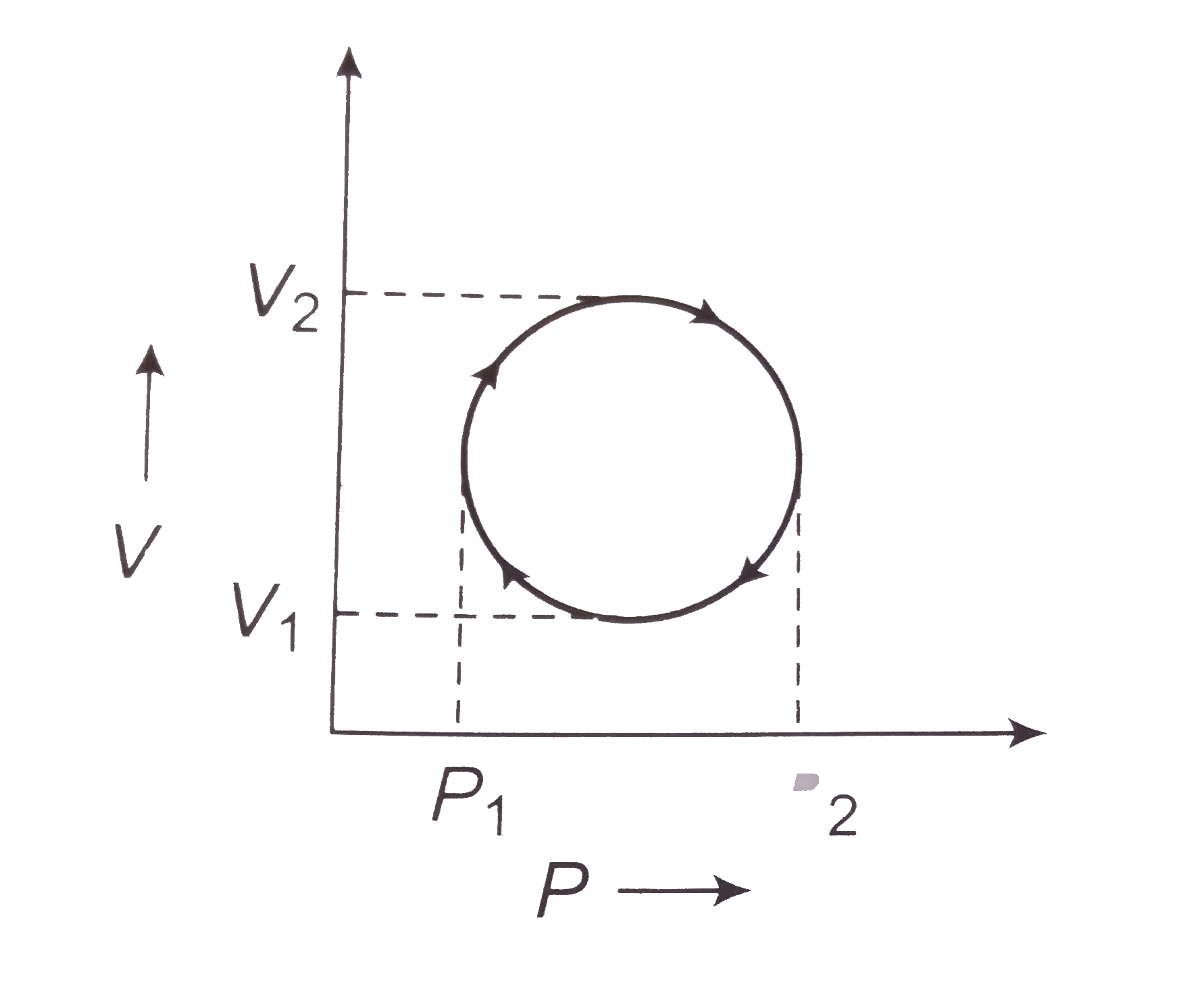
In the cyclic process shown in the `V-P` diagram the magnitude of the work is done is
View SolutionIn the previous question,
View Solution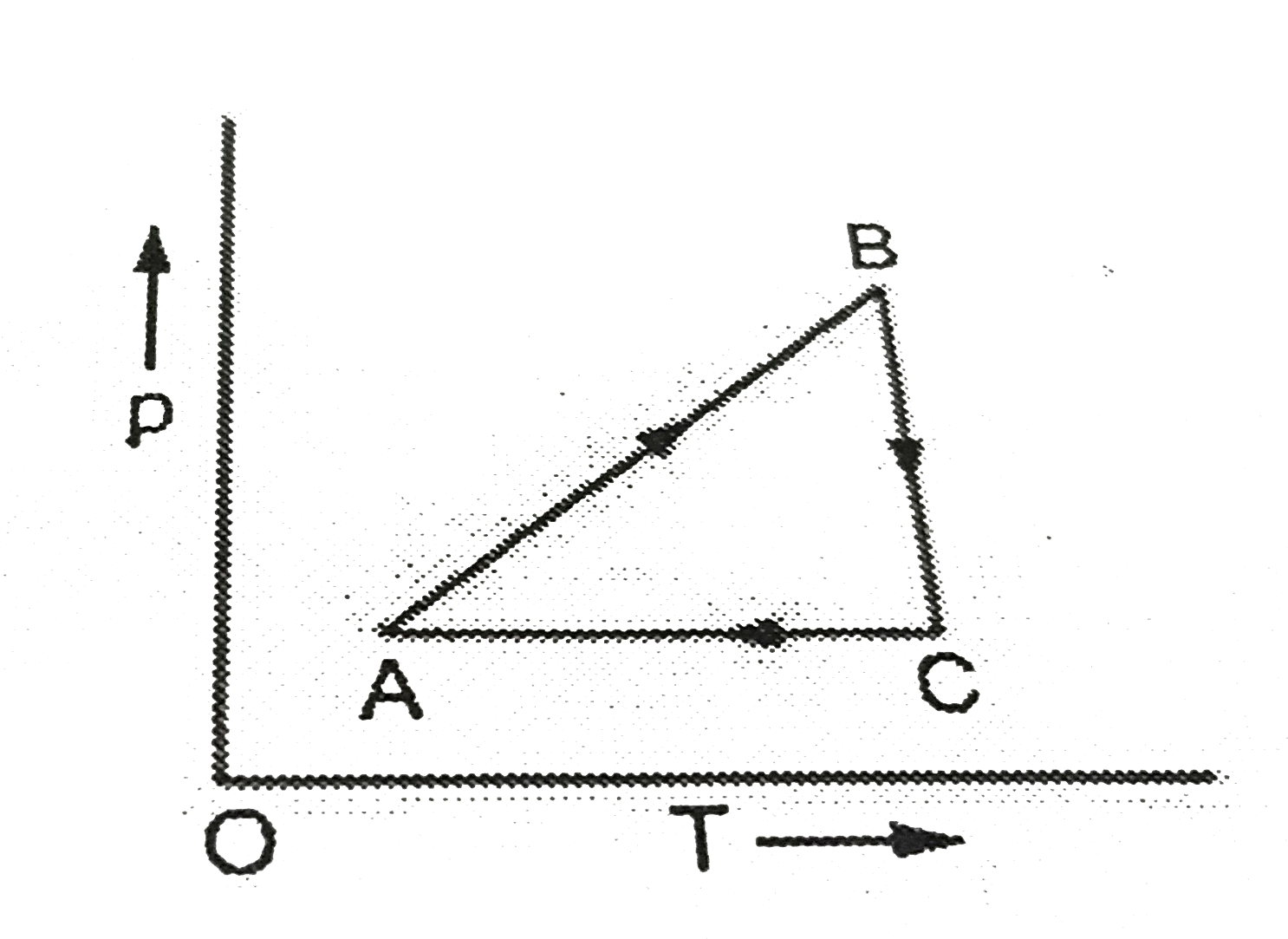
A cyclic process is shown in the p-T diagram. Which of the curves show the same process on a V-T diagram?
View Solution
A cyclic process is shown on the p-T diagram . Which of the curves show the same process on a V-T diagram?
View SolutionA cyclic process is shown in the `P-T` siagram. Whech of the curves show the same process on a `P-V` diagram ?
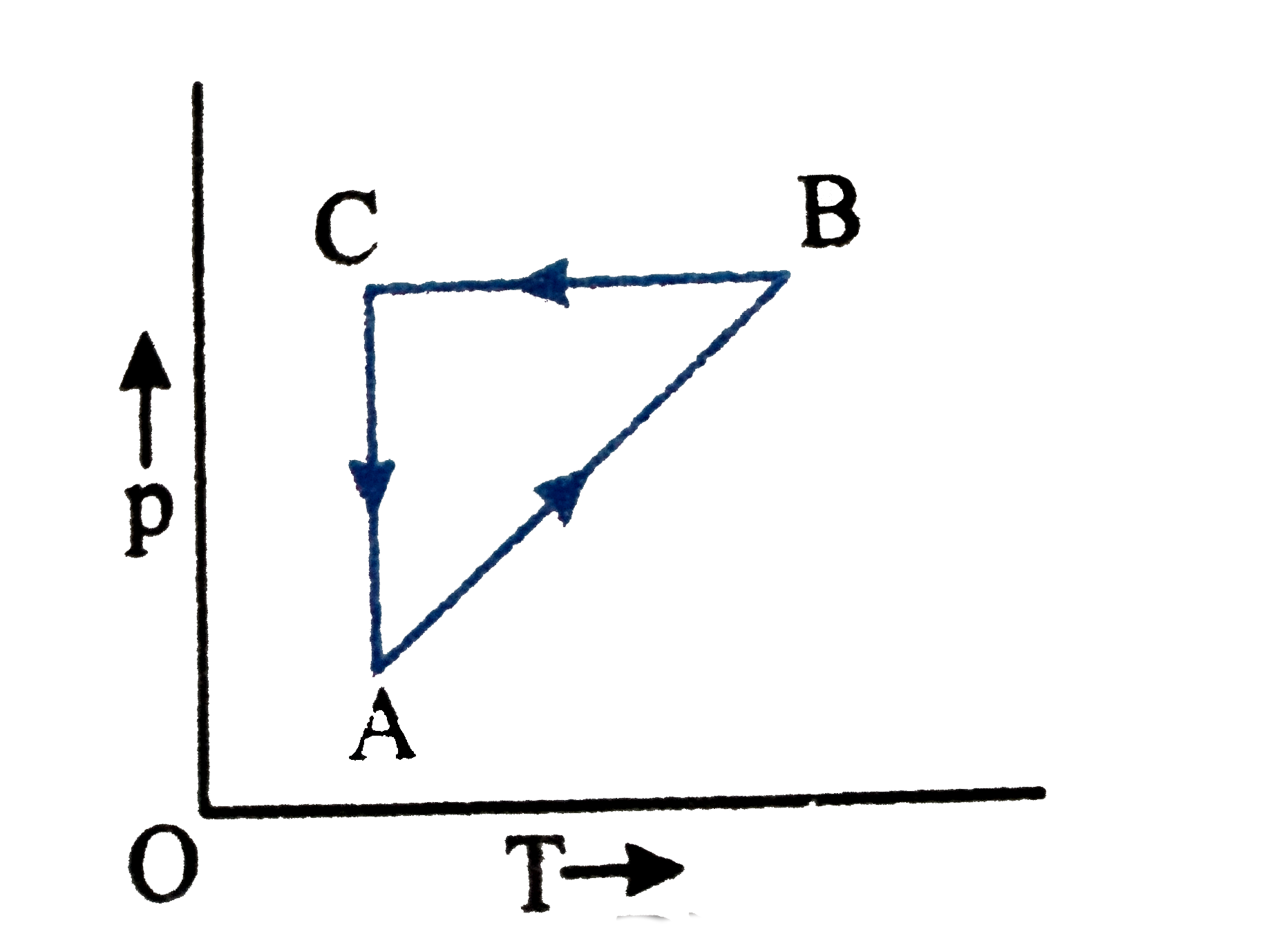
View SolutionThe first law of thermodynamics incorporates are concept of
(i) conservation of energy
(ii) convervation of heat
(iii) conservation of work
(iv) equivalence of heat and work
View SolutionStatement-I: it is possible for both the pressure and volume of a monoatomic ideal gas of a given amount to change simultaneously without causing the internal energy of the gas to change.
Statement-2: The internal energy of an ideal gas of a given amount remains constant it temperature does not change. it is possible to have a process in which pressure and volume are changed such that temperature remains constant.
View SolutionFor a ideal gas,
View SolutionThe molar heat capacity for an ideal gas cannot
View SolutionThe molar heat capacity for an ideal gas
View Solution`C_p` is always greater than `C_v` for a gas, which of the following statements provide, partly or wholly, the reason for this?
(i) No work is done by a gas at constant volume
(ii) When a gas absorbs heat at constant pressure, its volume must change
(iii) For the same change in temperature, the internal energy of a gas changes by a smaller amount at constant volume that at constant pressure
(iv) The internal energy of an ideal gas is a function only of its temperature
View SolutionA system undergoes a cyclic process in which it absorbs `Q_(1)` heat and gives out `Q_(2)` heat. The efficiency of the process is `eta` and work done is `W.` Select correct statement:
View Solution
Heat is supplied to a certain homogeneous sample of matter, at a uniform rate. Its temperature is plotted against time, as shown Which of the following conclusions can be drawn?
(i) Its specific heat capacity is greater in the solid state than the liquid state.
(ii) Its specific heat capacity is greater in the liquid state than in the solid state.
(iii) Its latent heat of vaporization is greater than its latent heat of fusion.
(iv) Its latent heat of vaporization is smaller than its latent heat of fusion
View SolutionThree rods of the same dimension have thermal conductivities 3K, 2K and K. They are arranged as shown in fig. with their ends at `100^(@)"C", 50^(@)"C and "20^(@)"C"`. The temperature of their junction is
View SolutionFive rods of same dimensions are arranged as shown in the figure. They have thermal conductivities `K _(1) , K_(2) , K _(3) , K_( 4)` and `K_( 5)` . When points A and B are maintained at different temperatures, no heat flows through the central rod if

View SolutionThree rods `A,B` and `C` have the same dimensions Their conductivities are `K_(A)` K and `K_(C)` respectively `A` and `B` are placed end to end with their free ends kept at certain temperature difference `C` is placed separately with its ends kept at same temperature difference The two arrangements conduct heat at the same rate `K_(c)` must be equal to .
View SolutionThree rods `A,B` and `C` have the same dimensions Their conductivities are `K_(A)` K and `K_(C)` respectively `A` and `B` are placed end to end with their free ends kept at certain temperature difference `C` is placed separately with its ends kept at same temperature difference The two arrangements conduct heat at the same rate `K_(c)` must be equal to .
View SolutionOne end of a uniform rod of length 10m is placed in boiling water while its other end is placed in melting ice. A point P on the rod is maintained at a constant temperature of `450^@C`. The mass of steam produced per second is equal to the mass of ice melted per second. If specific latent heat of steam is 7 times the specific latent heat of ice, the distance of P from the steam chamber must be___________(in m)
View Solution`A` and `B` are two points on uniform metal ring whose centre is `O` The angle `AOB =theta` A and `B` are maintaind at two different constant temperatures When `theta =180^(@)` the rate of total heat flow from `A` to `B` is `1.2W` When `theta =90^(@)` this rate will be .
View SolutionIn a 10 m deep lake, the bottom is at a constant temperature of `4^(@)C`. The air temperature is constant at `- 4^(@)C. K_(ice) = 3 K_(omega)`. Neglecting the expansion of water on freezing, the maximum thickness of ice will be
View SolutionA point source of heat of power P is placed at the centre of a spherical shell of mean radius R. The material of the shell has thermal conductivity K. If the temperature difference between the outer and inner surface of the shell in not to exceed T, the thickness of the shell should not be less than .......
View SolutionA spherical black body of radius `r` radiates power `P`, and its rate of cooling is `R`
(i)`P prop r`
(ii)`P prop r^(2)`
(iii)`R prop r^(2)`
(iv)`R prop (1)/(r)`
View SolutionThe temperature of an spherical isolated black body falls from `T_(1)` and `T_(2)` in time t them time t is
View SolutionA planet is at an average distance d from the sun and its average surface temeperature is T. Assume that the planet receives energy only from the sun and loses energy only through radiation from the surface. Neglect atmospheric effects. If `Tpropd^(-n)`, the value of n is
View SolutionThe solar constant for a planet is S. The surface temperature of the sun is TK. The sun subtends an angle `theta` at the planet:
View SolutionThe power radiated by a black body is P, and it radiates maximum energy around the wavelength `lambda_(0)`. If the temperature of the black body is now changed so that it radiates maximum energy around a wavelength `3lambda_(0)//4`, the power radiated by it will increase by a factor of
View SolutionTwo bodies A and B have thermal emissivities of 0.01 and 0.81 respectively. The outer surface areas of the two bodies are same. The two bodies emit total radiant power at the same rate. The wavelength `lambda_B` corresponding to maximum spectral radiancy from B is shifted from the wavelength corresponding to maximum spectral radiancy in the radiation from A by 1.0 `mum`. If the temperature of A is 5802 K, calculate (a) the temperature of B, (b) wavelength `lambda_B`.
View SolutionA black body is at a temperature of 2880 K. The energy of radiation emitted by this object with wavelength between 499 nm and 500 nm is`U_(1)`, between 999 nm and 1000 nm is `U_(2)` and between 1499 nm and 1500 nm is `U_(3)`. The Wein's constant `b = 2.88 xx 10^(6) "nm K"`. Then
View SolutionA body with an initial temperature `theta_(1)` is allowed to cool in a surrounding which is at a constant temperature of `theta_(0) (theta lt theta_(1))` Assume that Newton's law of cooling is obeyed Let `k =` constant The temperature of the body after time t is best experssed by .
View SolutionA system `S` receives heat continuously from an electric heater of power `10 W`. The temperature of `S` becomes constant at `50^(@)C` when the surrounding temperature is `20^(@)C`. After the heater is switched off, `S` cools from `35.1^(@)C` to `34.9^(@)C` in `1 minute`. the heat capacity of `S` is
View SolutionA body cools in a surrounding which is at constant temperature of `theta_(0)`. Assume that it obeys Newton's law of colling. Its temperature `theta` is plotted against time `t`. Tangents are drawn to the curve at the points `P(theta=theta_(t))` and `Q(theta=theta_(2))`. These tangents meet the time axis at angles of `phi_(2)` and `phi_(1)`, as shown
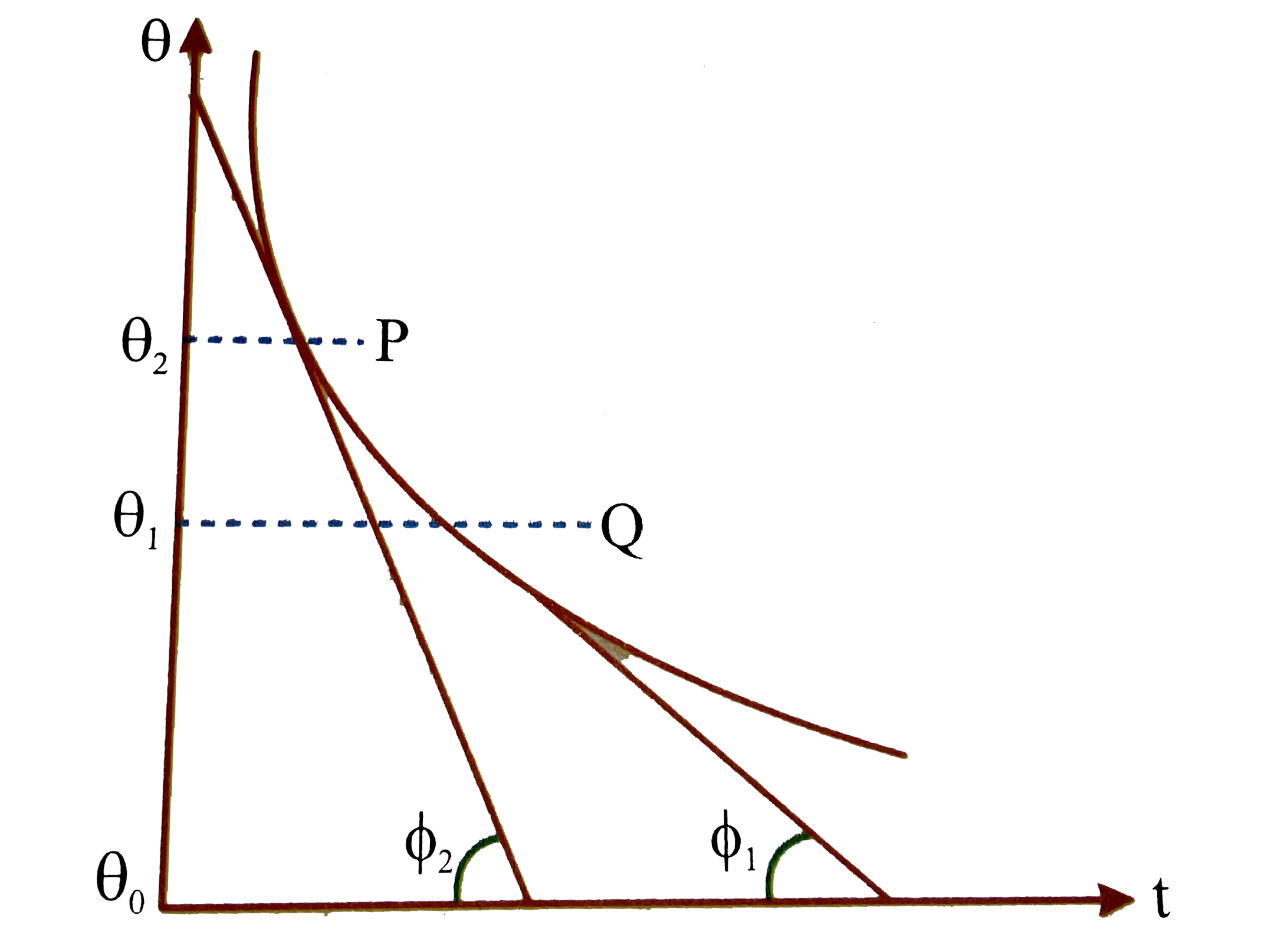
View Solution
All Questions questions and complete solutions for chapter HEAT AND THERMODYNAMICS of D MUKHERJEE PHYSICS (HINGLISH) of Class 12