Complete Solutions to प्रश्नावली 8B of chapter त्रिभुज of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | त्रिभुज |
| DAS GUPTA | प्रश्नावली 8B |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
रिक्त स्थानों की पूर्ति करें-
किसी त्रिभुज की समान भुजाओ के सम्मुख कोण……. होते है।03:39View Solutionरिक्त स्थानों की पूर्ति करें-
किसी त्रिभुज के समान कोणों की सम्मुख भुजाएँ …….. होती है।02:32View Solutionरिक्त स्थानों की पूर्ति करें-
यदि किसी त्रिभुज में दो कोण समान हो तो त्रिभुज…... होगा।02:01View Solutionरिक्त स्थानों की पूर्ति करें-
समबाहु त्रिभुज के प्रत्येक कोण की माप…….. होती है।02:14View Solutionरिक्त स्थानों की पूर्ति करें-
किसी समद्विबाहु त्रिभुज के आधार पर के कोण `alpha^(@)` और `beta^(@)` हो तो `alpha, beta` में संबंध…….. है।01:18View Solutionरिक्त स्थानों की पूर्ति करें-
त्रिभुज ABC में AB = AC और `angleB = 50^(@)` तो `angleA` की माप `= (….)^(@)`01:55View Solutionरिक्त स्थानों की पूर्ति करें-
किसी `DeltaABC` में AB = AC एवं `angleA = 100^(@)` है हो `angleB` की माप `= (….)^(@)`02:00View Solutionरिक्त स्थानों की पूर्ति करें-
यदि `DeltaABC` में `angleA = 50^(@), angleB = 80^(@)` हो तो यह…... त्रिभुज होगा।01:57View Solutionरिक्त स्थानों की पूर्ति करें-
समकोण समद्विबाहु त्रिभुज के किसी एक न्यूनकोण की माप `= (….)^(@)`02:10View Solutionरिक्त स्थानों की पूर्ति करें-
समकोण समद्विबाहु त्रिभुज के किसी एक न्यूनकोण की माप `= (…..)^(@)`01:57View Solutionरिक्त स्थानों की पूर्ति करें-
`DeltaABC` का `angleA = 90^(@)` तथा AB = AC है। AB को उसी सिद्द में D बिंदु तक बढ़ाया। `angleCBD` का मान अंशो में……. होगा।03:42View Solutionरिक्त स्थानों की पूर्ति करें-
यदि किसी समबाहु त्रिभुज की एक भुजा बढ़ाई जाए तो बहिष्कों की माप `= (….)^(@)`02:53View Solution`triangleABC` में AB = AC हो तो `alpha` का मान होगा?
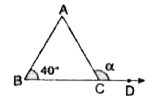 01:55View Solution
01:55View Solutionकिसी त्रिभुज के आधार को दोनों और बढ़ाने पर प्रत्येक बहिष्कों `135^(@)` का बनता है तो बताएँ की त्रिभुज निम्नलिखित में किस कोटि का है।
03:44View Solutionयदि दो समकोण त्रिभुजों में एक त्रिभुज की एक भुजा तथा एक न्यूनकोण दूसरे त्रिभुज की एक भुजा तथा तदनुरूपी कोण के बराबर हो तो दोनों त्रिभुज परस्पर क्या होंगे?
02:05View Solution`DeltaABC` और `DeltaPQR` में `angleA = angleP = 40^(@), AB = 4.5 cm, AC = 5cm` तथा `PQ = 4.5 cm, QR = 5cm` तो क्या दोनों त्रिभुज सर्वांगसम होंगे?
02:59View Solutionनिचे की आकृति में AB का लम्ब अर्द्धक CD है , सिद्ध करें कि `angleCAD=angleCBD`.
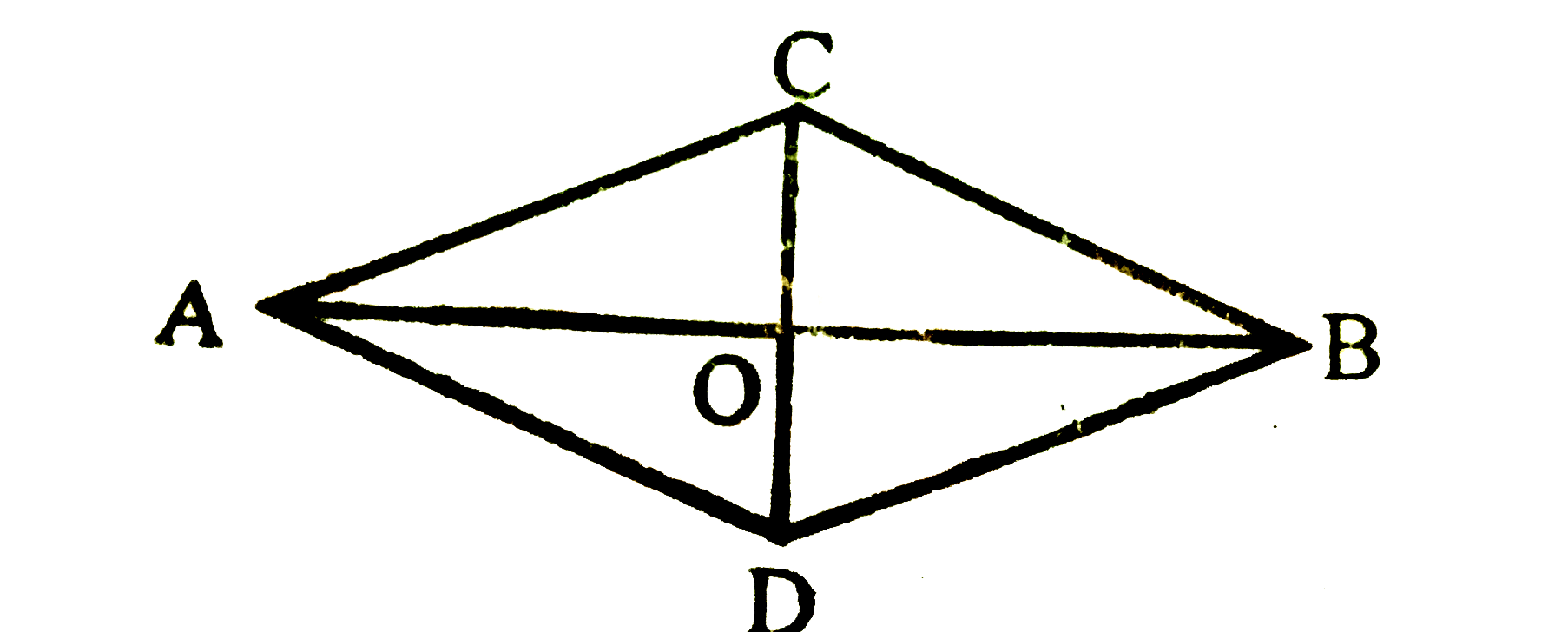 03:11View Solution
03:11View Solutionसमद्विबाहु त्रिभुज की बराबर भुजाओ में एक को आधार के सम्मूखशीर्ष की ओर बढ़ाया गया है। सिद्ध करें की बहिष्कों आधार-कोण का दुगुना है।
05:31View Solutionदी गयी आकृति में `PQ || SR` एवं `PS = PR` है I `alpha` एवं `beta` के मान ज्ञात करें।
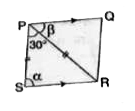 02:12View Solution
02:12View Solutionनिम्न आकृति में ABC एक समद्विबाहु त्रिभुज है जिसकी भुजा AB = भुजा AC और XY समान्तर हैं BC के | यदि `angleA=30^(@)` हो, तो `angleBXY` डिग्री में निकालें |
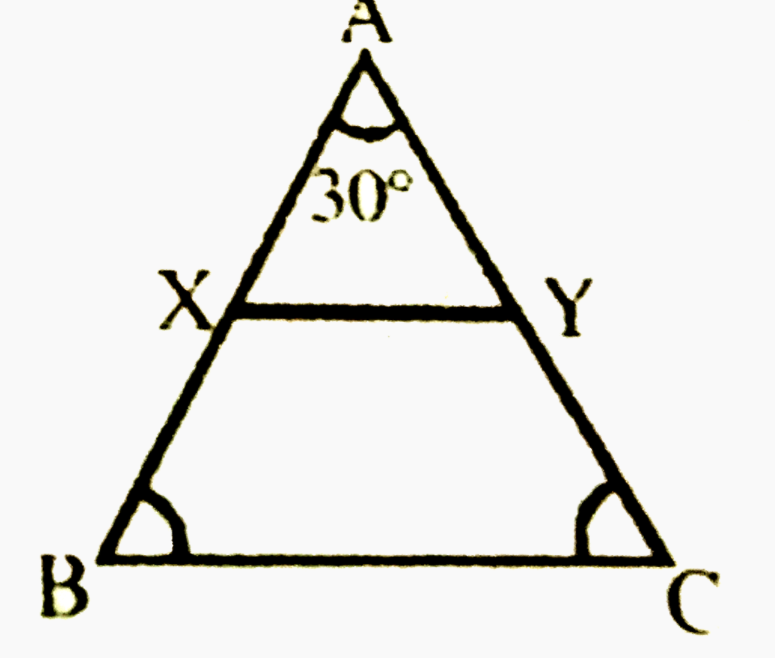 03:40View Solution
03:40View Solutionदो त्रिभुजों के सर्वांगसम होने की दो शर्त लिखे।
View Solutionरेखाखण्ड AB के विपरीत पक्षों में AX और BY समान लंबाई के दो रेखाखण्ड इस प्रकार है की `AX ||BY` रेखाखण्ड AB और XY एक-दूसरे को P पर काटते है तो सिद्ध करें की
`DeltaAPX ~= DeltaBPY`02:24View Solutionरेखाखण्ड AB के विपरीत पक्षों में AX और BY समान लंबाई के दो रेखाखण्ड इस प्रकार है की `AX ||BY` रेखाखण्ड AB और XY एक-दूसरे को P पर काटते है तो सिद्ध करें की
P, AB का मध्यबिंदु होगा।04:23View Solutionसिद्ध कीजिये की `DeltaABC` समद्विबाहु त्रिभुज होगा यदि
मध्यिका AD, आधार BC पर लंब हो।02:31View Solutionसिद्ध कीजिये की `DeltaABC` समद्विबाहु त्रिभुज होगा यदि
शीर्षकोण BAC का समद्विभाजक, आधार BC पर लंब हो।02:35View Solutionसिद्ध कीजिये की `DeltaABC` समद्विबाहु त्रिभुज होगा यदि
शीर्षलंब `AD, angleBAC` का समद्विभाजक हो।02:21View Solutionसिद्ध कीजिये की `DeltaABC` समद्विबाहु त्रिभुज होगा यदि
शीर्षलंब BE और CF समान हो।01:51View Solutionरेखा l, रेखांखण्ड BC का लंबसमद्विभाजक है। P, l पर कोई बिंदु है। सिद्ध करें कि PBC एक समद्विबाहु त्रिभुज होगा।
02:29View SolutionABC एक समद्विबाहु त्रिभुज है जिसमे बराबर भुजाएँ AC और AB पर क्रमश: शीर्षलंब BY और CZ खींचे गए है। दिखाएँ कि BY = CZ
02:03View Solutionयदि किसी समद्विबाहु त्रिभुज के शीर्षकोण को समद्विभाजित करनेवाली रेखा आधार को भी समद्विभाजित करे तो सिद्ध कीजिये कि वह रेखा आधार पर लंब होती है।
03:41View Solution`DeltaABC` में `angleA` का समद्विभाजक AD भुजा BC पर लंब है। सिद्ध कीजिये कि `DeltaABC` समद्विबाहु त्रिभुज है।
02:15View SolutionABC एक समद्विबाहु त्रिभुज है जिसकी AB भुजा =AC भुजा। ∠ B तथा ∠ C के समद्विभाजक O बिंदु पर काटते है। सिद्ध कीजिये कि OBC समद्विबाहु त्रिभुज है।
02:19View SolutionABC एक समद्विबाहु त्रिभुज है जिसकी AB भुजा = AC भुजा, `angleB` तथा `angleC` को BO तथा CO रेखाएं क्रमश: से समद्विभाजित करती है तो सिद्ध कीजिये कि
(i) BO = CO तथा (ii) `angleBAO = angleCAO`04:05View Solutionसमद्विबाहु त्रिभुज ABC ,∠BAC को AD समद्विभाजित करता है,D से समान भुजाओ पर लंब खाँचे जाएँ तो ये लंब बराबर होंगे।
02:25View SolutionABC एक समद्विबाहु त्रिभुज है जिसमे AB = AC, भुजा BA बिंदु D तक बढ़ाई गए है, ताकि AB = AD. सिद्ध करें की `angleBCD = 90^(@)`
02:15View Solutionसमद्विबाहु त्रिभुज की बराबर भुजाओ को एकही दिशा में बढ़ाने से आधार के नीचे जो कोण बनते है उनकी समद्विभाजक रेखाओ के मिलने से आधार के नीचे एक समद्विबाहु त्रिभुज बन जाता है, सिद्ध करे।
04:12View Solutionसिद्ध करें कि एक समकोण त्रिभुज में कर्ण का मध्यबिंदु तीनो शीर्ष से संदुरस्थ है।
07:06View Solution
प्रश्नावली 8B questions and complete solutions for chapter त्रिभुज of BHARATI BHAWAN MATHS (HINDI) of Class 12
