Complete Solutions to Level 1 Subjective of chapter MODERN PHYSICS - 1 of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MODERN PHYSICS - 1 |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
For a given element the wavelength of the `K_alpha`- line is 0.71 nm and of the `K_beta`- line it is 0.63 nm. Use this information to find wavelength of the `L_alpha` line.
View SolutionThe energy of the n=2 state in a given element is `E_2 =-2870 eV`. Given that the wavelengths of lthe `K_alpha` and `K_beta` lines are 0.71 nm and 0.63 nm respectively, determine the energies `E_1` and `E_3`.
View Solution1.5 mW of 400 nm light is directed at a photoelectric cell. If 0.1% of the incident photons produce photoelectrons, find the current in the cell.
View SolutionA photon has momentum of magnitude `8.24xx10^(-28) kg-m//s`. (a) What is the energy of this photon? Given your answer in joules and in electron volts
(b) What is the wavelength of this photon? In what region of the electormagnetic spectrum does lie?
View SolutionA 75 W light source emits light of wavelength 600 nm. (a) Calculate the frequency of the emitted light.
(b) How many photons per second does the source emit?
View SolutionAn excited nucleus emits a gamma-ray photon with energy of 2.45 MeV. (a) What is the photon frequency?
(b) what is the photon wavelength?
View Solution(a) A proton is moving at a speed much less than the speed of light. It has kinetic energy `K_1` and momentum `p_1`. If the momentum of the proton is doubled, so `p_2 = 2 p_1`, how is its new kinetic energy `K_2` related to `K-1`?
(b)A photon with energy `E_1` has momentum `p_1` . if another photon has momentum `p_2` that is twice `p_1`, how is the energy `E_2` of the second photon related to `E_1`?
View SolutionA parellel beam of monochromatic light of wavelength 500 nm is incident normally on a perfectly absorbing surface. The power through any cross section of the beam is 10 W. Find
(a) the number of photons absorbed per second by the surface and
(b) the force exerted by the light beam on the surface.
View SolutionA beam of white light is incident normaly on a plane surface absorbing 70% of the light and reflecting the rest. If the incident beam carries 10 w of power, find the force exerated by it on the surface.
View SolutionA parallel beam of monochromatic light of wavelength 663 nm is incident on a totally reflection plane mirror. The angle of incidence is `60^@` and the number of photons striking the mirror per second is `1.0xx10^19`. Calculate the force exerted by the light beam on the mirror.
View Solutionwavelength of Bullet. Calculate the de-Brogli wavelength of a 5.00 g bullet that is moving at 340 m/s will it exhibite wave like properties?
View Solution(a) An electron moves with a speed of `4.70xx10^6` m//s. What is its de-Broglie wavelength?
(b) A proton moves with the same speed. Determine its de - Broglie wavelength.
View SolutionAn electron has a de Broglie wavelength of `2.80xx10^(-10)` m. Determine (a) the magnitude of its momentum,
(b) its kinetci energy(in joule and in electron volt).
View SolutionFind de-Broglie wavelength corresponding to the root-mean square velocity of hydrogen molecules at room temperature `(20^@C)`.
View SolutionAn electron, in a hydrogen like atom , is in excited state. It has a total energy of -3.4 eV, find the de-Broglie wavelength of the electron.
View SolutionIn the Bohr model of the hydrogen atom, what is the de-Broglie wavelength for the electron when it is in (a) the n=1 level?
(b) Then n=4 level? In each case, compare the de-Broglie wavelength to the circumference `2pir_n` of the orbit.
View SolutionThe binding energy of an electron in the gorund state of He atom is equal to `E_0 = 24.6 eV.` Find the energy required to remove both electrons form the atom.
View SolutionHydrogen atom is its ground state is excited by means of monochromatic radiation of wavelength `1023 Å`. How many different lines are possible in the resulting spectrum? Calculate the longes wavelength among them. You may assume the ionization energy of hydrogen atom as 13.6 eV.
View SolutionA doubly ionized lithium atom is hydrogen like with atomic number 3. Find the wavelength of the radiation required to excite the electron in `Li^(++)` from to the third Bohr orbit (ionization energy of the hydrogen atom equals 13.6 eV).
View SolutionFind the quantum number n corresponding to nth excited state of `He^(++)` ion if on transition to the ground state the ion emits two photons in succession with wavelength 108.5 nm and 30.4 nm. The ionization energy of the hydrogen atom is 13.6 eV.
View SolutionA hydrogen like atom (described by the Bohr model) is observed ot emit ten wavelengths, originating from all possible transition between a group of levels. These levels have energies between - 0.85 eV and -0.544 eV (including both these values). (a) Find the atomic number of the atom.
(b) Calculate the smallest wavelength emitted in these transitions. (Take ground state energy of hydrogen atom =- 13.6 eV)
View SolutionThe energy levels of a hypothetical one electron atom are shown in the figure. (a)Find the ionization potential of this atom.
(b) Find the short wavelength limit of the series terminating at n=2
(c ) Find the excitaion potential for the state n=3.
(d) find wave number of the photon emitted for the transiton n=3 to n=1 `prop _______________ 0eV`
`n=5 __________________ -0.80 eV`
n=4 ______________ -1.45 eV`
n=3__________________ -3.08 eV`
n=2_______________ -5.30 eV`
`n=1 ____________________ -15.6 eV`.
View Solution(a) An atom initally in an energy level with E = - 6.52 eV absorbs a photon that has wavelength 860 nm. What is the internal energy of the atom after it absorbs the photon?
(b) An atom initially in anergy level with E =-2.68 ev emits a photon that has wavelength 420 nm. What is the internal energy of the atom after it emits the photon?
View SolutionA silver balll is suspended by a string in a vacuum chamber and ultraviolet light of wavelength `2000 Å` is directed at it. What electrical potential will the ball acquire as a result? Work function of silver is 4.3 eV.
View SolutionA small particle of mass m move in such a way the potential energy `(U = (1)/(2) m^(2) omega^(2) r^(2))` when a is a constant and r is the distance of the particle from the origin Assuming Bohr's model of quantization of angular momentum and circular orbits , show that radius of the nth allowed orbit is proportional to in
View SolutionWavelength of `K_alpha` line of an element is `lambda_0`. Find wavelength of `K_beta` - line for the same elemetn.
View Solutionx-rays are produced in an X-ray tube by electrons asselerated through an electric potential difference fo 50.0 kV. An electron makes three collisions in the target coming to rest and loses half its remaining kinetic energy in each of the first two collisions. Determine the wavelenght of the resulting photons. (Neglecting the recoil of the heavey target atoms).
View SolutionFrom what meterial is the anod of an X-ray tube made if the `K_alpha` line wavelength of thej characteristic spectrum is `0.76 Å`?
View SolutionThe short-wavelength limit shifts by 26 pm when the operating voltage in an X-ray tube is increased to 1.5 times the original value. What was the original value of the operating voltage?
View SolutionThe `k_alpha` X-rays of aluminium (Z = 13 ) and zinc ( Z = 30) have wavelengths 887 pm and 146 pm respectively. Use Moseley\'s law `sqrt v = a(Z - b)` to find the wavelength of the `K_alpha` X-ray of iron (Z = 26).
View SolutionCharacteristic X-rays of frequency `4.2xx10^18` Hz are produced when transitions from L-shell to K-shell take place in a certain target material. Use Mosley's law to determine the atomic number of the target material. Given Rydberg constant `R =1.1xx10^7 m^(-1)`.
View SolutionThe electric current in an X-ray tube (from the target to the filament) operating at `40 kV `is `10 mA`. Assume that on an average, 1% of the total kinetic energy of the electrons hitting the target are converted into X-rays (a) what is the total power emitted as X-rays and (b) how much heat is produced in the target every second?
View SolutionThe stopping potential for the photoelectrons emitted from a metal surface of work function 1.7 eV is 10.4 V. Find the wavelength of the radiaiton used. Also, identify the energy levels in hydrogen atom, which will emit this wavelength.
View SolutionWhat will be the maximum kinetic energy of the photoelectrons ejected from magnesium (for which the work -function W=3.7 eV) when irradiated by ultraviolet light of frequency `1.5xx10^15 s^(-1)`.
View SolutionA metallic surface is irradiated with monochromatic light of variable wavelength. Above a wavelength of `5000 Å` no photoelectrons are emitted from the surface. With an unknown wavelength, stopping potential fo 3V is neceddsry ot eliminate the photocurrent. Find the unknown wavelenght.
View SolutionA graph regarding photoelectric effect is shown between the maximum kinetic energy of electrons and the frequency of the incident light. On the basis of data as shown in the graph, calculate (a) threshold frequency , (b) work- function, (c ) planck constant
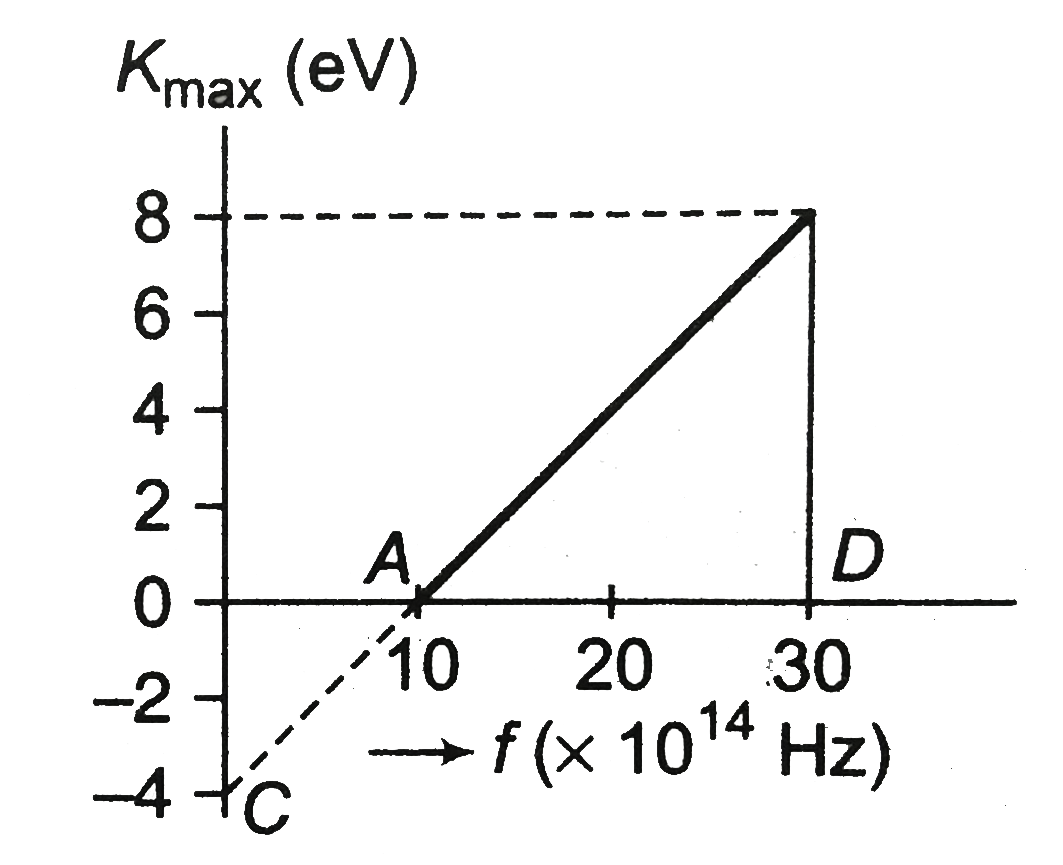
View SolutionA metallic surface is illuminated alternatively with light of wavelenghts `3000 Å` and `6000 Å`. It is observed that the maximum speeds of the photoelectrons under these illuminations are in the ratio 3 : 1 . Calculate the work function of the metal and the maximum speed of the photoelectrons in two cases.
View SolutionLight of wavelength 180 nm ejects photoelectrons from a plate of metal whose work - function is 2 eV. If a uniform magnetic field of `5xx10^(-5)` T be applied parllel to the palte, what would be the radius of the path followed by electrons ejected normally from the plate with maximum energy.
View SolutionLight described at a palce by te equation `E=(100 V/m) [sinxx10^15 s ^(-1) t +sin (8xx 10^15 s^(-1) t]` falls on a metal surface having work function 2.0 eV. Calcualte the maximum kinetic energy of the photoelectrons.
View SolutionThe electric field associated with a light wave is given by `E= E_0 sin [(1.57x 10^7 m^(-1)(x-ct)].` Find the stopping potential when this light is used in an experiment on photoelectric affect with a metal having work - function 1.9 eV.
View Solution
Level 1 Subjective questions and complete solutions for chapter MODERN PHYSICS - 1 of DC PANDEY PHYSICS (HINGLISH) of Class 12
All Exercises from DC PANDEY Class 12 PHYSICS MODERN PHYSICS - 1
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Exercise 33.1
- Exercise 33.2
- Exercise 33.3
- Exercise 33.4
- Level -1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Based
- Level 2 More Than One Correct
- Level 2 Passage 3
- Level 2 Passage 4
- Level 2 Single Correct
- Level 2 Subjective
- Level 2Passage 2
- Miscellaneous Examples