Complete Solutions to Physics of chapter PRACTICAL PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | PRACTICAL PHYSICS |
| DISHA | Physics |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
To calculate an unknown resistance with the help of a meter bridge why is it advised to change the gap with the known and unknown resistance?
View SolutionPotential gradient of a potentiometer is equal to
View SolutionThe refractive index of the material of a prism does not depend on which of the following factor?
View SolutionA meter-bridge is based on the principle of
View SolutionA potentiometer works on the principle that
View SolutionWhich of the following operations will not increase the sensitivity of a potentiometer?
View SolutionWhich two circuit components are connected in parallel in the following circuit diagram ?
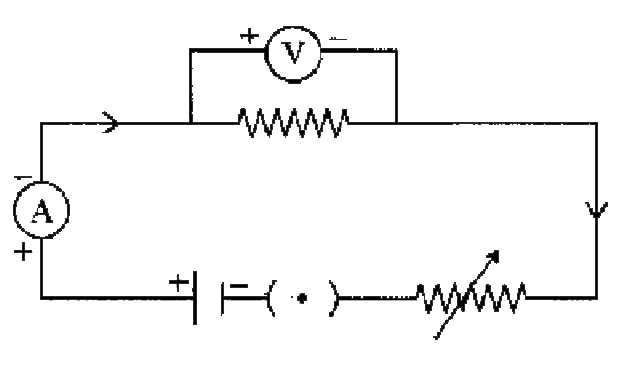
View SolutionA current of 4A produces a deflection of `30°` in the galvanometer. The figure of merit is
View SolutionThe potential gradient of a potentiometer can be increased by which of the following operation?
View SolutionOf the diodes shown in the following diagrams, which one is reverse biased?
View SolutionTo determine the equivalent resistance of two resistors when connected in series, a student arranged the circuit components as shown in (Fig. 3.63) But he did not succeed to achieve the objective. Which mistake has been committed by him in setting up the circuit ?
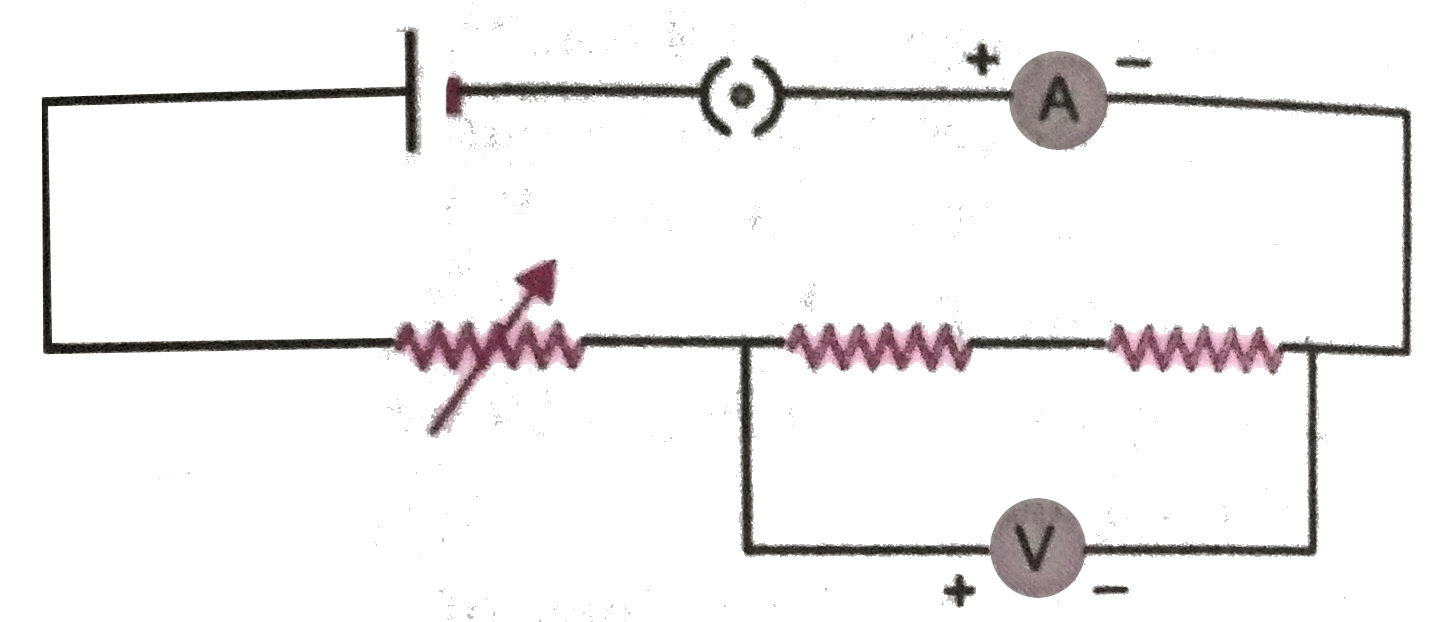 .
.
View SolutionIn the circuit shown, voltmeter is ideal and its least count is 0.1 V. The least count of ammeter is 1 mA. Let reading of the voltmeter be `30.0 V` and the reading of ammeter is `0.020 A`. Calculate the value of resistance R within error limits.
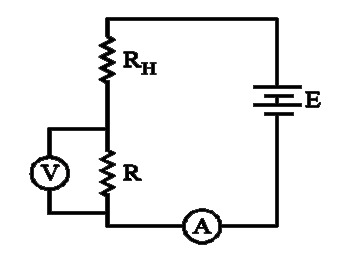
View SolutionIn an experiment to measure the focal length of a concave mirror. If was found that for an object distance of 0.30 m, the image distance come out to be 0.60 m. Let us determine the focal length.
View SolutionIn an experiment to determine an unknown resistance, a 100 cm long rets tance wire is used. The unknown resistance is kept in the left gap and a known resistance is put into the right gap. The scale to measure length has a least count 1 mm. The null point B is obtained at 40.0 cm from the left gap. We shell determine the percentage error in the computation of unknown resistance.
View SolutionIn an experiment to determine the focal length `(f)` of a concave mirror by the `u-v` method, a student places the object pin A on the principal axis at a distance x from the pole P. The student looks at the pin and its inverted image from a distance keeping his/her eye in line with PA. When the student shifts his/her eye towards left, the image appears to the right of the object pin. Then,
View SolutionIf the wire in the experiment to determine the resistivity of a material using meter bridge is replaced by copper or hollow wire the balance point i.e. null point shifts to
View SolutionConsider a block of conducting material of resistivity `'rho'` shown in the figure. Current `'I'` enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage `DeltaV` developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law `E = rhoj,` where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
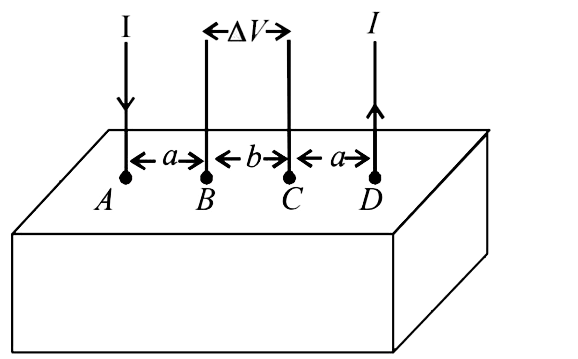
For current entering at A, the electric field at a distance 'r'
View SolutionConsider a block of conducting material of resistivity `'rho'` shown in the figure. Current `'I'` enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage `DeltaV` developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law `E = rhoj,` where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.

For current entering at A, the electric field at a distance 'r'
View SolutionOn cm on the main scale of vernier callipers is divided into ten equal parts. If 20 division of vernier scale coincide with 8 small divisions of the main scale. What will be the least count of callipers ?
View SolutionThe shape of stress vs strain graph within elastic limit is :
View SolutionIn a vernier calliper, N divisions of vernier scale coincide with (N-1) divisions of main scale (in which division represent 1mm). The least count of the instrument in cm. should be
View SolutionIn an experiment for measurement of young's modulus, following readings are taken. Load = 3.00 kg, length = 2.820 m, diameter = 0.041 cm and extension = 0.87. We shell determine the percentage error in measurement of Y.
View SolutionThe least count of a spherometer is given by
View SolutionWhich principle is involved in the experiment to determine the specific heat of a liquid by the method of mixture ?
View SolutionTwo full turns of the circular scale of a screw gauge cover a distance of `1mm` on its main scale. The total number of divisions on the circular scale is `50`. Further, it is found that the screw gauge has a zero error of `- 0.03mm`. While main scale reading of `3mm` and the number of circular scale divisions in line with the main scale as `35`. the dimeter of the wire is
View Solutionin an experiment the angles are required to be using an instrument, `29` divisions of the main scale exactly coincide with the `30` divisions of the vernier scale. If the sallest division of the main scale is half- a degree `(= 0.5^(@)`, then the least count of the instrument is :
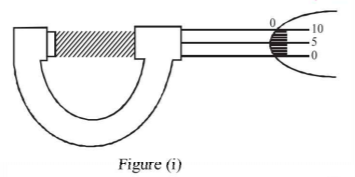
View SolutionIn a screw gauge, the zero of mainscale coincides with fifth division of circular scale in figure (i). The circular division of screw gauge are `50`. It moves `0.5 mm` on main scale In one rotation. The diameter of the ball in figure (ii) is

View SolutionA student performs an experiment an for determination of `g(=(4pi^(2)l)/(T^(2)))`. The error in length `l` is `Deltal` and in time `T` is `DeltaT and n` is number of times the reading is taken. The measurment of `g` is most accurate for
View SolutionA student performs an experiment to determine the Young's modulus of a wire, exactly`2m` long, by Searle's method. In a partcular reading, the student measures the extension in the length of the wire to be `0.8mm with an uncertainty of `+- 0.05mm` at a load of exactly `1.0kg`, the student also measures the diameter of the wire to be `04mm` with an uncertainty of `+-0.01mm`. Take `g=9.8m//s^(2)` (exact). the Young's modulus obtained from the reading is
View SolutionStudent `I ,II , and III` perform an experiment for measuring the acceleration due to gravity `(g) ` usinf a simple pendulum. They use lengths of the pendulum and // or record time for different number of oscillations . The observations are shown in the following table . Least count for length ` = 0.1 cm`
`{:(underset(III)underset(II)underset(I)underset()underset()("Student"),underset(20.0)underset(64.0)underset(64.0)underset((cm))underset("Pendulam")("Length of "),underset(4)underset(4)underset(8)underset((n))underset("n Oscillation")("Number of"),underset(9.0)underset(16.0)underset(16.0)underset((s))underset("Period")("Time")):}`
Least count for time `= 0.1 s`.
If `E_(I), E_(II)` , and `E_(III)` are the percentage errors in `g` , i.,e., `((Delta g)/( g) xx 100)` for students I,II , and III, respectively , then
View SolutionIf the terminal speed of a sphere of gold (density `=19.5kg//m^3`) is `0.2m//s` in a viscous liquid (density `=1.5kg//m^3`), find the terminal speed of a sphere of silver (density `=10.5kg//m^3`) of the same size in the same liquid
View SolutionA spherical solild of volume V is made of a material of density `rho_(1)`. It is falling through a liquid of density `rho_(2)(rho_(2) lt rho_(1))`. Assume that the liquid applies a viscous froce on the ball that is proportional ti the its speed v, i.e., `F_(viscous)=-kv^(2)(kgt0)`. The terminal speed of the ball is
View Solution
A jar filled with two non-mixing liquid 1 and 2 having densities `rho_(1)` and `rho_(2)` respectively. A solid ball, made of a material of density `rho_(3)` is dropped in the jar. It come to equilibrium in the position shown in the figure. Which of the following is true for `rho_(1),rho_(2)` and `rho_(3)`?
View SolutionA capillary tube (A) is dipped in water. Another identical tube (B) is dipped in a soap-water solution. Which of the following shows the relative nature of the liquid columns in the two tubes?
View SolutionTwo wires are made of the same material and have the same volume. However wire 1 has cross-sectional area A and wire 2 has cross-sectional area 3A. If the length of wire 1 increases by `Deltax` on applying force F, how much force is needed to stretch wire 2 by the same amount?
View SolutionThe vernier constant of a Vernier Callipers `A` and `B` are `0.01 cm` and `0.01 mm` respectively. The one which can measure the length of a small cylinder more accurately is
View SolutionIf x, y, p and q represent the increase in length, the original length of the experimental wire, load applied to the wire and area of cross-section of the wire respectively then Young's modulus of the wire is given by
View Solution
Physics questions and complete solutions for chapter PRACTICAL PHYSICS of DISHA PHYSICS (HINGLISH) of Class 12