Complete Solutions to JEE section (Comprehension type questions) of chapter THERMODYNAMICS AND THERMOCHEMISTRY of Class 12 book with complete answers and questions
| Class 12 | CHEMISTRY |
| Chapter | THERMODYNAMICS AND THERMOCHEMISTRY |
| ERRORLESS | JEE section (Comprehension type questions) |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
A fixed mass m of a gas is subjected to transformation of states from K to L to M to N and back to K as shown in the figure.
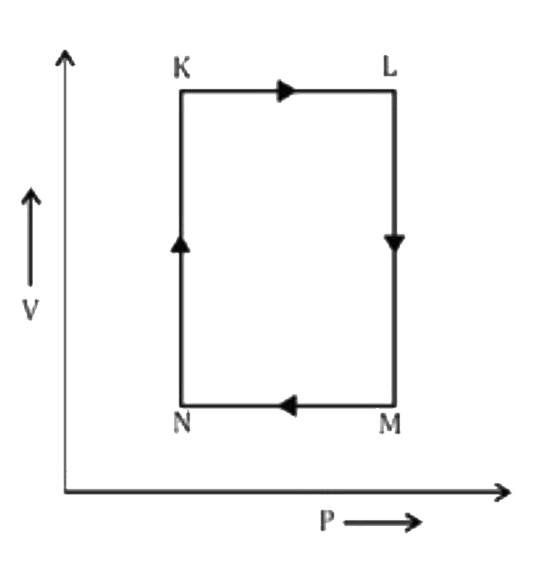
The succeeding operation that enable this transformation of state are03:30View SolutionA fixed mass 'm' of a gas is subjected to transformation of states from K to L to M to N and back to K as shown in the figure
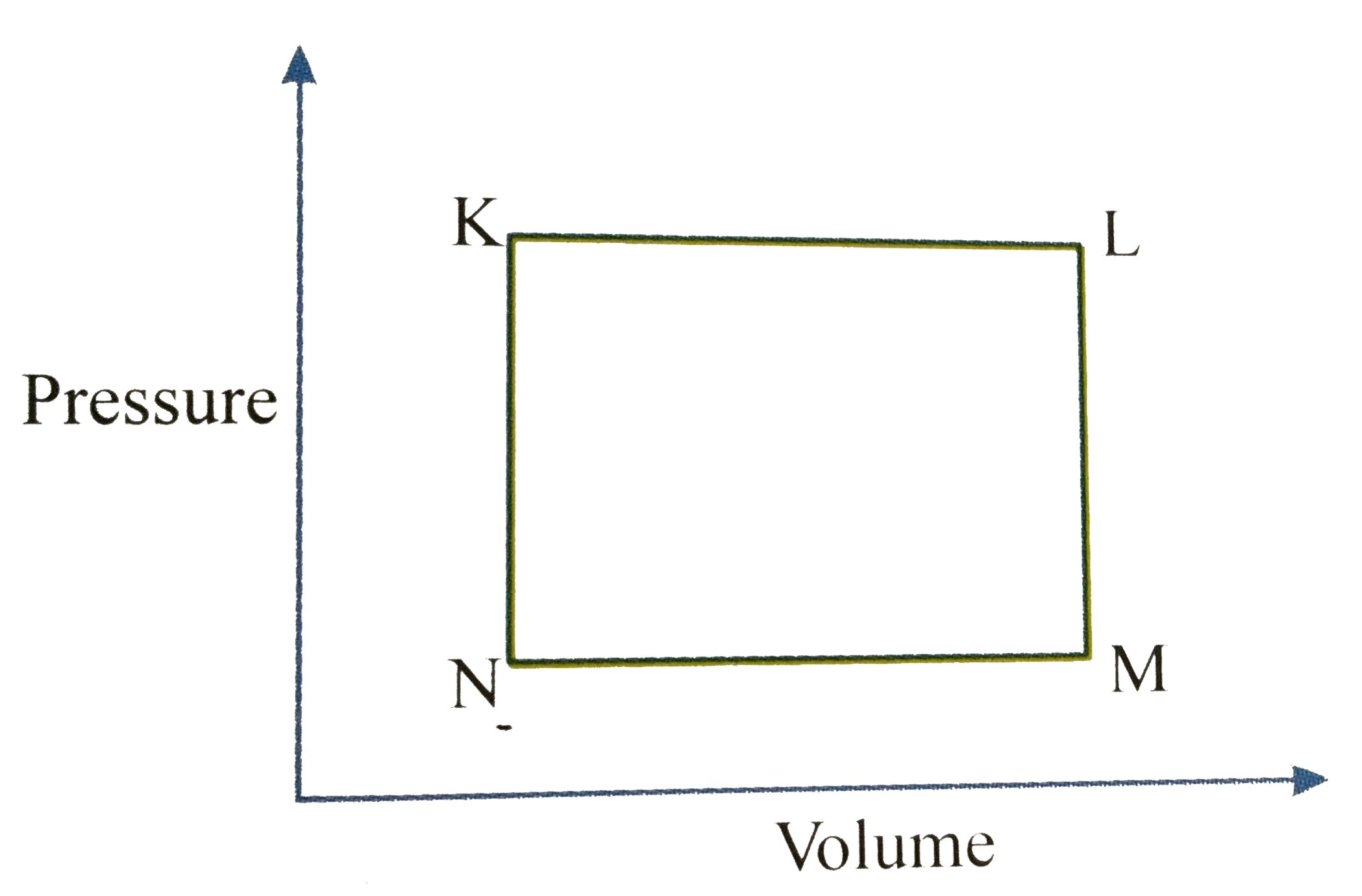
The pair of isochoric process among the tranformation of states is01:18View SolutionWhen 100 mL of 1.0 M HCl was mixed 100 mL of 1.0 M NaOH in an insulated beaker at constant pressure, a temperature increase `5.7^(@)C` was measured for the beaker and its contents (Expt. 1). Because the enthalpy of neutralization of a strong acid with a strong base is a constant `(-57.0 kJmol^(-1))`, this experiment could be used to measure the calorimeter constant. In a second experiment (Expt.2) 100 mL of 2.0 M acetic acid `(K_(a)=2.0xx10^(-5))` was mixed with 100 mL of 1.0 M NaOH (under indentical conditions to Expt. 1) where a temperature rise of `5.6^(@)C` was measured
(Consider heat capacity of all solutions as `4.2 Jg^(-1)K^(-1)` and density of al solutions as 1.0 gm`L^(-1)`)
Enthalpy of dissociation (in `KJmol^(-1)`) of acetic acid obtained from the Expt.2 isView SolutionWhen 100 mL of 1.0 M HCl was mixed 100 mL of 1.0 M NaOH in an insulated beaker at constant pressure, a temperature increase `5.7^(@)C` was measured for the beaker and its contents (Expt. 1). Because the enthalpy of neutralization of a strong acid with a strong base is a constant `(-57.0 kJmol^(-1))`, this experiment could be used to measure the calorimeter constant. In a second experiment (Expt.2) 100 mL of 2.0 M acetic acid `(K_(a)=2.0xx10^(-5))` was mixed with 100 mL of 1.0 M NaOH (under indentical conditions to Expt. 1) where a temperature rise of `5.6^(@)C` was measured
(Consider heat capacity of all solutions as `4.2 Jg^(-1)K^(-1)` and density of al solutions as 1.0 gm`L^(-1)`)
The pH of the solution after Expt. 2 isView SolutionStandard Gibb's energy of reaction `(Delta_(r)G^(@))` at a certain temperature can be computed as `Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows
`Delta_(r)H_(T_(2))^(@)-Delta_(r)H_(T_(1))^(@)=Delta_(r)C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r)S_(T_(2))^(@)-Delta_(r)S_(T_(1))^(@)=Delta_(r)C_(p)^(@)ln((T_(2))/(T_(1)))`
`Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
`"and by "Delta_(r)G^(@)=-RT lnK_(eq)`
Consider the following reaction :
`CO(g)+2H_(2)(g)subCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH),g=-201 kJ//mol`
`Delta_(f)H^(@)(CO, g)=-114 kJ//mol`
`S^(@)(CH_(3)OH, g)=240 J//K-mol, S^(@)(H_(2),g)=29 JK^(-1)mol^(-1)`
`S^(@)(CO, g)=198 J//mol-K, C_(p,m)^(@)(H_(2))=28.8J//mol-K`
`C_(p,m)^(@)(CO)=29.4 J//mol-K, C_(p,m)^(@)(CH_(3)OH)=44 J//mol-K`
and `ln((320)/(300))0.06`, all data at 300 K
`Delta_(r)S^(@)` at 320 K isView SolutionStandard Gibb's energy of reaction `(Delta_(r)G^(@))` at a certain temperature can be computed as `Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows
`Delta_(r)H_(T_(2))^(@)-Delta_(r)H_(T_(1))^(@)=Delta_(r)C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r)S_(T_(2))^(@)-Delta_(r)S_(T_(1))^(@)=Delta_(r)C_(p)^(@)ln((T_(2))/(T_(1)))`
`Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
`"and by "Delta_(r)G^(@)=-RT lnK_(eq)`
Consider the following reaction :
`CO(g)+2H_(2)(g)subCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH),g=-201 kJ//mol`
`Delta_(f)H^(@)(CO, g)=-114 kJ//mol`
`S^(@)(CH_(3)OH, g)=240 J//K-mol, S^(@)(H_(2),g)=29 JK^(-1)mol^(-1)`
`S^(@)(CO, g)=198 J//mol-K, C_(p,m)^(@)(H_(2))=28.8J//mol-K`
`C_(p,m)^(@)(CO)=29.4 J//mol-K, C_(p,m)^(@)(CH_(3)OH)=44 J//mol-K`
and `ln((320)/(300))0.06`, all data at 300 K
`Delta_(r)S^(@)` at 300 K for the reaction isView SolutionStandard Gibb's energy of reaction `(Delta_(r)G^(@))` at a certain temperature can be computed as `Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows
`Delta_(r)H_(T_(2))^(@)-Delta_(r)H_(T_(1))^(@)=Delta_(r)C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r)S_(T_(2))^(@)-Delta_(r)S_(T_(1))^(@)=Delta_(r)C_(p)^(@)ln((T_(2))/(T_(1)))`
`Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
`"and by "Delta_(r)G^(@)=-RT lnK_(eq)`
Consider the following reaction :
`CO(g)+2H_(2)(g)subCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH),g=-201 kJ//mol`
`Delta_(f)H^(@)(CO, g)=-114 kJ//mol`
`S^(@)(CH_(3)OH, g)=240 J//K-mol, S^(@)(H_(2),g)=29 JK^(-1)mol^(-1)`
`S^(@)(CO, g)=198 J//mol-K, C_(p,m)^(@)(H_(2))=28.8J//mol-K`
`C_(p,m)^(@)(CO)=29.4 J//mol-K, C_(p,m)^(@)(CH_(3)OH)=44 J//mol-K`
and `ln((320)/(300))0.06`, all data at 300 K
`Delta_(r)H^(@)` at 320 K isView SolutionStandard Gibb's energy of reaction `(Delta_(r)G^(@))` at a certain temperature can be computed as `Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows
`Delta_(r)H_(T_(2))^(@)-Delta_(r)H_(T_(1))^(@)=Delta_(r)C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r)S_(T_(2))^(@)-Delta_(r)S_(T_(1))^(@)=Delta_(r)C_(p)^(@)ln((T_(2))/(T_(1)))`
`Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
`"and by "Delta_(r)G^(@)=-RT lnK_(eq)`
Consider the following reaction :
`CO(g)+2H_(2)(g)subCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH),g=-201 kJ//mol`
`Delta_(f)H^(@)(CO, g)=-114 kJ//mol`
`S^(@)(CH_(3)OH, g)=240 J//K-mol, S^(@)(H_(2),g)=29 JK^(-1)mol^(-1)`
`S^(@)(CO, g)=198 J//mol-K, C_(p,m)^(@)(H_(2))=28.8J//mol-K`
`C_(p,m)^(@)(CO)=29.4 J//mol-K, C_(p,m)^(@)(CH_(3)OH)=44 J//mol-K`
and `ln((320)/(300))0.06`, all data at 300 K
`Delta_(r)H^(@)` at 300 K for the reaction isView SolutionStandard Gibb's energy of reaction `(Delta_(r)G^(@))` at a certain temperature can be computed as `Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)` and the change in the value of `Delta_(r)H^(@)` and `Delta_(r)S^(@)` for a reaction with temperature can be computed as follows
`Delta_(r)H_(T_(2))^(@)-Delta_(r)H_(T_(1))^(@)=Delta_(r)C_(p)^(@)(T_(2)-T_(1))`
`Delta_(r)S_(T_(2))^(@)-Delta_(r)S_(T_(1))^(@)=Delta_(r)C_(p)^(@)ln((T_(2))/(T_(1)))`
`Delta_(r)G^(@)=Delta_(r)H^(@)-T.Delta_(r)S^(@)`
`"and by "Delta_(r)G^(@)=-RT lnK_(eq)`
Consider the following reaction :
`CO(g)+2H_(2)(g)subCH_(3)OH(g)`
Given : `Delta_(f)H^(@)(CH_(3)OH),g=-201 kJ//mol`
`Delta_(f)H^(@)(CO, g)=-114 kJ//mol`
`S^(@)(CH_(3)OH, g)=240 J//K-mol, S^(@)(H_(2),g)=29 JK^(-1)mol^(-1)`
`S^(@)(CO, g)=198 J//mol-K, C_(p,m)^(@)(H_(2))=28.8J//mol-K`
`C_(p,m)^(@)(CO)=29.4 J//mol-K, C_(p,m)^(@)(CH_(3)OH)=44 J//mol-K`
and `ln((320)/(300))0.06`, all data at 300 K
`Delta_(r)G^(@)` at 320 K isView Solution
JEE section (Comprehension type questions) questions and complete solutions for chapter THERMODYNAMICS AND THERMOCHEMISTRY of UNIVERSAL BOOK DEPOT 1960 CHEMISTRY (HINGLISH) of Class 12
All Exercises from ERRORLESS Class 12 CHEMISTRY THERMODYNAMICS AND THERMOCHEMISTRY
- Critical Thinking (Objective Questions)
- JEE section (Comprehension type questions)
- JEE section (Integer type questions)
- JEE section (JEE (Advanced) 2018) More than one choice correct answer
- JEE section (JEE (Advanced) 2018) Numeric answer type questions
- JEE section (Matrix Match type questions)
- JEE section (More than one choice correct answer)
- JEE section (Only one correct answer)
- JEE section (Reasoning type questions)
- ORDINARY THINKING (Objective Questions) Bond energy
- ORDINARY THINKING (Objective Questions) Free energy and Work function
- ORDINARY THINKING (Objective Questions) Heat of reaction
- ORDINARY THINKING (Objective Questions) Basic Concepts
- ORDINARY THINKING (Objective Questions) First law of thermodynamics and Hess law
